12.8: Using Symmetry to Predict Zero in a Secular Determinant
- Page ID
- 204001
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As we continue with this course, we will discover that there are many times when we would like to know whether a particular integral is necessarily zero, or whether there is a chance that it may be non-zero. We can often use group theory to differentiate these two cases.
You will have already used symmetry properties of functions to determine whether or not a one-dimensional integral is zero. For example, cos(x) is an ‘even’ function (symmetric with respect to reflection through the origin), and it follows from this that
\[\int^{\infty}_{-\infty} \cos(x) dx = 0 \nonumber \]
In general integral between these limits for any other even function will be also be zero.
In the general case we may have an integral of more than one dimension. The key to determining whether a general integral is necessarily zero lies in the fact that because an integral is just a number, it must be invariant to any symmetry operation. For example, bonding in a diatomic (see next section) depends on the presence of a non-zero overlap between atomic orbitals on adjacent atoms, which may be quantified by an overlap integral. You would not expect the bonding in a molecule to change if you rotated the molecule through some angle \(\theta\), so the integral must be invariant to rotation, and indeed to any other symmetry operation.
In group theoretical terms, for an integral to be non-zero, the integrand must transform as the totally symmetric irreducible representation in the appropriate point group. In practice, the integrand may not transform as a single irreducible representation, but it must include the totally symmetric irreducible representation. These ideas should become more clear in the next section.
It should be noted that even when the irreducible representations spanned by the integrand do include the totally symmetric irreducible representation, it is still possible for the integral to be zero. All group theory allows us to do is identify integrals that are necessarily zero based on the symmetry (or lack thereof) of the integrand.
Secular Equations
As we have seen already, any set of linear equations may be rewritten as a matrix equation \(A\textbf{x}\) = \(\textbf{b}\). Linear equations are classified as simultaneous linear equations or homogeneous linear equations, depending on whether the vector \(\textbf{b}\) is non-zero or zero. For a set of simultaneous linear equations (non-zero \(\textbf{b}\)) it is fairly apparent that if a unique solution exists, it can be found by multiplying both sides by the inverse matrix \(A^{-1}\) (since \(A^{-1}A\) on the left hand side is equal to the identity matrix, which has no effect on the vector \(\textbf{x}\))
\[\begin{array}{rcl} A\textbf{x} & = & \textbf{b} \\ A^{-1}A\textbf{x} & = & A^{-1}\textbf{b} \\ \textbf{x} & = & A^{-1}\textbf{b} \end{array} \label{21.1} \]
In practice, there are easier matrix methods for solving simultaneous equations than finding the inverse matrix, but these need not concern us here. We previously argued that in order for a matrix to have an inverse, it must have a non-zero determinant. Since \(A^{-1}\) must exist in order for a set of simultaneous linear equations to have a solution, this means that the determinant of the matrix \(A\) must be non-zero for the equations to be solvable.
For a matrix to have an inverse, it must have a non-zero determinant.
The reverse is true for homogeneous linear equations. In this case the set of equations only has a solution if the determinant of \(A\) is equal to zero. The secular equations we want to solve are homogeneous equations, and we will use this property of the determinant to determine the molecular orbital energies. An important property of homogeneous equations is that if a vector \(\textbf{x}\) is a solution, so is any multiple of \(\textbf{x}\), meaning that the solutions (the molecular orbitals) can be normalized without causing any problems.
Solving for the orbital energies and expansion coefficients
Recall the secular equations for the \(A_1\) orbitals of \(NH_3\) derived in the previous section
\[\begin{array}{rcl} c_1(H_{11} - ES_{11}) + c_2(H_{12} - ES_{12}) & = & 0 \\ c_1(H_{12} - ES_{12}) + c_2(H_{22} - ES_{22}) & = & 0 \end{array} \label{21.2} \]
where \(c_1\) and \(c_2\) are the coefficients in the linear combination of the SALCs \(\phi_1\) = \(s_N\) and \(\phi_2\) = \(\dfrac{1}{\sqrt{3}}(s_1 + s_2 + s_3)\) used to construct the molecular orbital. Writing this set of homogeneous linear equations in matrix form gives
\[\begin{pmatrix} H_{11} - ES_{11} & H_{12} - ES_{12} \\ H_{12} - ES_{12} & H_{22} - ES_{22} \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \label{21.3} \]
In order for the equations to have a solution, the determinant of the matrix must be equal to zero. Writing out the determinant will give us a polynomial equation in \(E\) that we can solve to obtain the orbital energies in terms of the Hamiltonian matrix elements \(H_{ij}\) and overlap integrals \(S_{ij}\). The number of energies obtained by ‘solving the secular determinant’ in this way is equal to the order of the matrix, in this case two.
The secular determinant for Equation (21.3) is (noting that \(S_{11}\) = \(S_{22} = 1\) since the SALCs are normalized)
\[(H_{11} - E)(H_{22} - E) - (H_{12} - ES_{12})^2 = 0 \label{21.4} \]
Expanding and collecting terms in \(E\) gives
\[E^2(1-S_{12}^2) + E(2H_{12}S_{12} - H_{11} - H_{22}) + (H_{11}H_{22} - H_{12}^2) = 0 \label{21.5} \]
which can be solved using the quadratic formula to give the energies of the two molecular orbitals.
\[E_\pm = \dfrac{-(2H_{12}S_{12} - H_{11} - H_{22}) \pm \sqrt{(2H_{12}S_{12} - H_{11} - H_{22})^2 - 4(1-S_{12}^2)(H_{11}H_{22} - H_{12}^2)}}{2(1-S_{12}^2)} \label{21.6} \]
To obtain numerical values for the energies, we need to evaluate the integrals \(H_{11}\), \(H_{22}\), \(H_{12}\), and \(S_{12}\). This would be quite a challenge to do analytically, but luckily there are a number of computer programs that can be used to calculate the integrals. One such program gives the following values.
\[\begin{array}{rcl} H_{11} & = & -26.0000 \: eV \\ H_{22} & = & -22.2216 \: eV \\ H_{12} & = & -29.7670 \: eV \\ S_{12} & = & \: 0.8167 \: eV \end{array} \label{21.7} \]
When we substitute these into our equation for the energy levels, we get:
\[\begin{array}{rcl} E_+ & = & \: 29.8336 \: eV \\ E_- & = & -31.0063 \: eV \end{array} \label{21.8} \]
We now have the orbital energies and the next step is to find the orbital coefficients. The coefficients for an orbital of energy \(E\) are found by substituting the energy into the secular equations and solving for the coefficients \(c_i\). Since the two secular equations are not linearly independent (i.e. they are effectively only one equation), when we solve them to find the coefficients what we will end up with is the relative values of the coefficients. This is true in general: in a system with \(N\) coefficients, solving the secular equations will allow all \(N\) of the coefficients \(c_i\) to be obtained in terms of, say, \(c_1\). The absolute values of the coefficients are found by normalizing the wavefunction.
Since the secular equations for the orbitals of energy \(E_+\) and \(E_-\) are not linearly independent, we can choose to solve either one of them to find the orbital coefficients. We will choose the first.
\[(H_{11} - E_{\pm})c_1 + (H_{12} - E_{\pm}S_{12})c_2 = 0 \label{21.9} \]
For the orbital with energy \(E_-\) = -31.0063 eV, substituting numerical values into this equation gives
\[\begin{array}{rcl} 5.0063 c_1 - 4.4442 c_2 & = & 0 \\ c_2 & = & 1.1265 c_1 \end{array} \label{21.10} \]
The molecular orbital is therefore
\[\Psi = c_1(\phi_1 + 1.1265\phi_2) \label{21.11} \]
Normalizing to find the constant \(c_1\) (by requiring \(<\Psi|\Psi>\) = 1) gives
\[\begin{array}{rcll} \Psi_1 & = & 0.4933\phi_1 + 0.5557\phi_2 & \\ & = & 0.4933s_N + 0.3208(s_1 + s_2 + s_3) & (\text{substituting the SALCs for} \: \phi_1 \: \text{and} \: \phi_2) \end{array} \label{21.12} \]
For the second orbital, with energy \(E_+\) = 29.8336 eV, the secular equation is
\[\begin{array}{rcl} -55.8336c_1 - 54.1321c_2 & = & 0 \\ c_2 & = & -1.0314c_1 \end{array} \label{21.13} \]
giving
\[\begin{array}{rcll} \Psi_2 & = & c_1(\phi_1 - 1.0314\phi_2) & \\ & = & 1.6242\phi_1 - 1.6752\phi_2 & \text{(after normalization)} \\ & = & 1.6242s_N -0.9672(s_1 + s_2 + s_3) \end{array} \label{21.14} \]
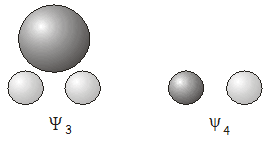
These two \(A_1\) molecular orbitals \(\Psi_1\) and \(\Psi_2\), one bonding and one antibonding, are shown below.

The remaining two SALCs arising from the \(s\) orbitals of \(NH_3\) (\(\phi_3 = \dfrac{1}{\sqrt{6}}\begin{pmatrix} 2s_1 - s_2 - s_3 \end{pmatrix}\) and \(\phi_4 = \dfrac{1}{\sqrt{2}}\begin{pmatrix} s_2 - s_3 \end{pmatrix}\)), form an orthogonal pair of molecular orbitals of \(E\) symmetry. We can show this by solving the secular determinant to find the orbital energies. The secular equations in this case are:
\[\begin{array}{rcl} c_1(H_{33} - ES_{33}) + c_2(H_{34} -ES_{34}) & = & 0 \\ c_1(H_{34} -ES_{34}) + c_2(H_{44} - ES_{44}) & = & 0 \end{array} \label{21.15} \]
Solving the secular determinant gives
\[E_\pm = \dfrac{-(2H_{34}S_{34} - H_{33} - H_{44}) \pm \sqrt{(2H_{34}S_{34} - H_{33} - H_{44})^2 - 4(1-S_{34}^2)(H_{33}H_{44} - H_{34}^2)}}{2(1-S_{34}^2)} \label{21.16} \]
The integrals required are
\[\begin{array}{rcl} H_{33} & = & -9.2892 \: eV \\ H_{44} & = & -9.2892 \: eV \\ H_{34} & = & 0 \\ S_{34} & = & 0 \end{array} \label{21.17} \]
Using the fact that \(H_{34}\) = \(S_{34} = 0\), the expression for the energies reduces to
\[E_\pm = \dfrac{(H_{33} + H_{44}) \pm (H_{33} - H_{44})}{2} \label{21.18} \]
giving \(E_+\) = \(H_{33}\) = -9.2892 eV and \(E_-\) = \(H_{44}\) = -9.2892 eV. Each SALC therefore forms a molecular orbital by itself, and the two orbitals have the same energy; the two SALCs form an orthogonal pair of degenerate orbitals. These two molecular orbitals of \(E\) symmetry are shown below.
- Choose a basis set of functions \(f_i\) consisting of the valence atomic orbitals on each atom in the system, or some chosen subset of these orbitals.
- With the help of the appropriate character table, determine which irreducible representations are spanned by the basis set using Equation (15.20) to determine the number of times \(a_k\) that the \(k^{th}\) irreducible representation appears in the representation. \[a_k = \dfrac{1}{h}\sum_C n_C \chi(g) \chi_k(g) \label{22.1} \]
- Construct the SALCs \(\phi_i\) that transform as each irreducible representation using Equation 16.1 \[\phi_i = \sum_g \chi_k(g) g f_i \label{22.2} \]
- Write down expressions for the molecular orbitals by taking linear combinations of all the irreducible representations of the same symmetry species.
- Write down the secular equations for the system.
- Solve the secular determinant to obtain the energies of the molecular orbitals.
- Substitute each energy in turn back into the secular equations and solve to obtain the coefficients appearing in your molecular orbital expressions in step 4.
- Normalize the orbitals.

