Homework 15

Last updated
Save as PDF

Page ID: 204099

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Q1

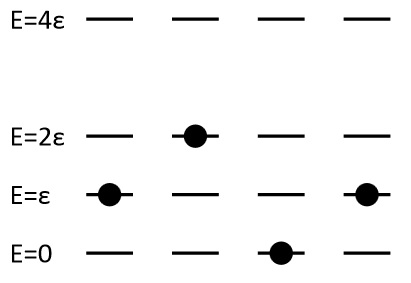
If four distinguishable particles can each occupy energy levels 0, \(\epsilon\), \(2\epsilon\), and \(4\epsilon\). Calculate the entropy of the system if the total energy is

\(3\epsilon\)
\(4\epsilon\)
\(8\epsilon\)
\(12\epsilon\)
\(16\epsilon\)

One possible configuration for \(4\epsilon\);

Q2

Consider a system of \(N\) distinguishable,independent particles, each of which has only two accessible states; a ground state of energy 0 and an excited state of energy \(ε\). If the system is in equilibrium with a heat bath of temperature \(T\), calculate \(A\) ,\(U\), \(S\), and \(C_v\). Sketch \(C_v\) versus \(T\). How your results would change if \(ε_o\) were added to both energy values (i.e., a change in the zero of energy like a zero point energy) ?

Q3

Calculate the value of \(n_x\), \(n_y\), \(n_z\) for the case \(n_x = n_y = n_z\) for a hydrogen atom in a box of dimension \(1\; cm^3\) if the particle has kinetic energy \(3k_BT/2\) for T =27 ºC. What significant fact does this calculation illustrate? How would this change if we considered a hydrogen molecule instead?

Q4

Molecular nitrogen is heated in an electric arc and it is found spectroscopically that the (non-relative) populations of excited vibrational levels are

v=0	v= 1	v= 2	v= 3	v= 4
1.00	0.2	0.04	0.008	0.005

Is the nitrogen in thermodynamic equilibrium with respect to vibrational energy? What is the vibrational temperature of the gas? Is this necessarily the same as the translational temperature?

Q5

What is the entropy of 1 mole of helium at 298 K and 1 atm.

Q6

Consider the gas phase \(N_2\) molecule at a temperature of 300 K.

What is the most probable value of the rotational quantum number \(J\) if one ignores the fact that \(N_2\) is homonuclear?
Determine the fraction of molecules in each \(J\) state from 0 to 9 at T=300 K ( just use the high temperature limit for \(q_{rot}\) in these calculations). Compare your results with what you determined in part a.
What is the most probable vibrational quantum number \(v\) for this same temperature?