2: The Density of Liquids and Solids (Experiment)
- Page ID
- 221122
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
- To determine the density of pure water;
- To determine the density of aluminum (applying the technique of water displacement) and to use this value to determine the thickness of a piece of aluminum foil;
- To measure the mass and volume (via measured dimensions) of several cylinders of an unknown material, and to determine the density of this material via graphical analysis of the collected data.
Density
Density is defined as the mass per unit volume of a substance, and it is a physical property of matter. A physical property can be measured without changing the chemical identity of the substance. Since pure substances have unique density values, measuring the density of a substance can help identify that substance. Density is determined by dividing the mass of a substance by its volume:
\[Density = \frac{Mass}{Volume}\]
The units of density are commonly expressed as g/cm3 for solids, g/mL for liquids, and g/L for gases.
Density is also an intensive property of matter. This means that the value of density is independent of the quantity of matter present. For example, the density of a gold coin and a gold statue are the same, even though the gold statue consists of the greater quantity of gold. This is in contrast to extensive properties, like volume (the amount of space occupied by matter), which depend of the quantity of mater present. The more matter present, the larger the volume.
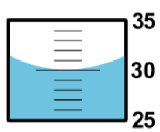
In Part A of this lab, the mass and volume of distilled water will be measured in order to determine the density of water. Measurements will be performed on three samples of water to improve precision and accuracy. Mass will be measured with an electronic balance, in grams (g), and volume will be measured directly with a graduated cylinder, in milliliters (mL). Recall that when measuring liquid volumes, the graduated scale must be read from the lowest point of the curved surface of the liquid (the meniscus).
The accuracy of the experimentally determined density of water will then be evaluated by comparison to the true, accepted density of water.
Measuring the Volume of a Liquid
The graduated cylinder markings are every 1-milliliter. When read from the lowest point of the meniscus, the correct reading is 30.0 mL. The first 2 digits 30.0 are known exactly. The last digit 30.0 is uncertain. Even though it is a zero, it is significant and must be recorded.
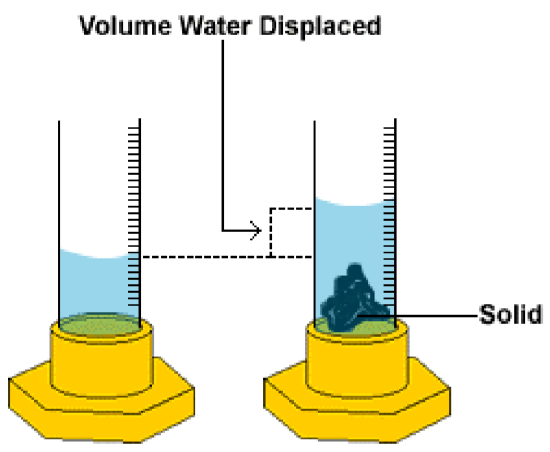
In Part B of this lab, the density of aluminum will be determined using aluminum pellets. Again, mass will be measured using an electronic balance, in grams (g). However, since the pellets have irregular shapes, their volume must be measured indirectly using the technique of water displacement (also known as Archimedes Principle). This is because the volume of water that the solid displaces when it is immersed in the water is the same as the volume of the solid itself. The accuracy of this experimentally determined density will also be evaluated by comparison to the true, accepted density of aluminum.
Measuring the Volume of an Irregularly Shaped Solid
\[\text{Volume water displaced} = \text{Final volume } – \text{Initial volume}\]
\[\text{Volume water displaced} = \text{Volume of solid}\]
Note that 1 mL = 1 cm3.
The density of aluminum will then be used in an applied problem to determine the thickness of a piece of aluminum foil. The piece of foil used can be considered to be a very flat rectangular box, where
\[\text{Volume of foil} = length \times width \times thickness\]
The foil volume can be obtained from the measured mass of the foil and the density of aluminum. Thus, if the length and width of the foil rectangle are measured, then the foil’s thickness may be calculated.
Density and Graphical Analysis
Laboratory investigations involve collecting data, which is often numeric. One common method of interpreting data is graphical analysis.
In Part C of this lab, the mass and volume of several cylindrical pieces of an unknown solid material will be measured. Once again mass will be obtained using an electronic balance, in grams (g). But since the cylinders are regularly-shaped solids, their volumes (in cubic centimeters, cm3) will be calculated from their measured dimensions by using the appropriate volume formula:
\[\text{Volume of a cylinder} = 2 \pi r h\]
\[h = \text{cylinder height or length}\]
\[r = \text{cylinder radius } = \frac{1}{2} \text{ the diameter}\]
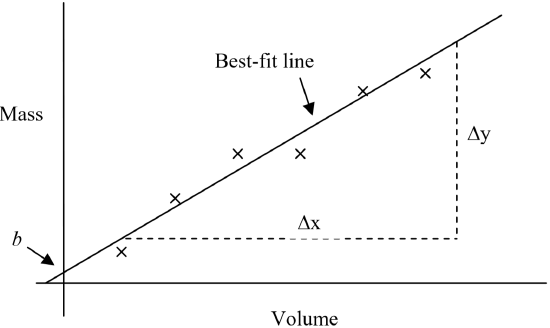
Each pair of mass and volume values will then be plotted on graph paper as a scatter plot, with mass plotted on the y-axis and volume plotted on the x-axis. Since the plotted data generate (or at least approximate) a straight line, a “best-fit line” can be added to the graph. A best-fit line is a single line that comes as close as possible to all the plotted points.
The equation of this best-fit line will have the familiar form \(y = mx + b\), where \(m\) represents the slope of the line, and \(b\) represents the y-intercept. This is illustrated in the figure below.
Best-fit line equation:
\[y = mx + b\]
where
- \(b\) is the y-intercept and
- \(m\) is the slope
The y-intercept (\(b\)) is the point on the y-axis where the line crosses the axis. In this experiment, the value of \(b\) should be equal to zero. This is because if there is no mass, the volume must also be zero. However, note that your best-fit line might not pass exactly through the origin (0,0) due to experimental error – but it should be quite close.
The slope of the line (\(m\)) is the change in the y-axis values divided by the change in x-axis values (or, rise over run):
\[\begin{align*} m &= \frac{ \Delta y}{ \Delta x} \\[5pt] &= \frac{y_1 − y_2}{x_1−x_2} \end{align*} \]
Since \( \Delta y\) is really the change in mass (\(\Delta \text{mass}\)), and \(\Delta x\) is really the change in volume (\( \Delta \text{volume}\)), this means that the slope of the best-fit line yields the density of the unknown material:
\[m = \frac{\Delta y}{\Delta x} = \frac{\Delta \text{mass}}{ \Delta \text{volume}} = \text{density}\]
Once the density is determined in this manner, it will be used to identify the unknown material analyzed.
Procedure
Materials and Equipment
100-mL graduated cylinder, metric ruler*, aluminum pellets, small beaker, aluminum foil, thermometer, electronic balance, distilled water, tube of unknown solid cylinders* and graph paper.
Safety
Be especially careful when adding the aluminum to your graduated cylinder, as the glass could break. Tilt the graduated cylinder and allow the pellets to gently slide to the bottom.
Part A: The Density of Water
- Using the electronic balance, obtain the mass of your 100-mL graduated cylinder. Make sure it is dry before you weigh it.
- Add 20-25 mL of distilled water to the graduated cylinder. Precisely measure this volume of water. Then measure the combined mass using the electronic balance.
- Add another 20-25 mL of distilled water to the graduated cylinder. Again, precisely measure this volume of water, and then measure the combined mass using the electronic balance.
- Repeat Step 3 to obtain a third set of mass and volume measurements.
- Use your thermometer to record the temperature of the water in your graduated cylinder.
- Analysis: Subtract the mass of the empty cylinder from each combined mass measurement to obtain three mass measurements of water. Use the three sets of mass and volume measurements to calculate three density values for water. Then take the average of these three density values. Finally, look up the true density of water at the temperature used, and evaluate the accuracy of your average density value by calculating your percent error.
Part B: The Density of Aluminum and the Thickness of Foil
The Density of Aluminum
- Using the electronic balance, obtain the mass of a clean, dry small beaker.
- Obtain a sample of aluminum from your instructor. Transfer all the pellets to the beaker, and measure the mass of the beaker and pellets.
- Pour 30-35 mL of water into your 100-mL graduated cylinder. Precisely measure this volume.
- Carefully add all the aluminum pellets to the water, making sure not to lose any water to splashing. Also make sure that the pellets are all completely immersed in the water. Measure the new volume of the water plus the pellets.
- When finished, retrieve and dry the aluminum pellets and return them to your instructor.
- Analysis: Use your measured mass and volume (obtained via water displacement) of the aluminum pellets to calculate the density of aluminum. Then look up the true density of aluminum and evaluate your accuracy by calculating your percent error.
The Thickness of Aluminum Foil
- Now obtain a rectangular piece of aluminum foil from your instructor. Use the ruler to measure the length and width of the piece of foil.
- Measure the mass of the foil using the electronic balance.
- When finished, return the foil to your instructor and the ruler to the stockroom.
- Analysis: Use these measurements along with the density of aluminum to calculate the thickness of the foil.
Part C: Graphical Analysis of Mass and Volume Data of an Unknown Solid
- Check out a ruler from the stockroom and obtain a tube containing cylindrical pieces of an unknown solid material from your instructor. Record the ID Code of the unknown solid on your report form.
- Using the ruler, measure the dimensions (diameter and height) of each cylindrical object. Start with the smallest object first and progress in order of increasing object size.
- Measure the mass of each cylindrical object using an electronic balance. Again, start with the smallest object first and progress in order of increasing object size.
- Replace all the objects in the tube and return the tube to your instructor.
- Analysis: Use the measured dimensions to calculate the volume of each solid object. Then, on the graph paper supplied, plot the mass (Y) versus the volume (X) of each measured object. Add a best- fit line to this plot. Calculate the slope of this line, which is the density of the unknown solid. Then use this density to identify the unknown material analyzed. Your unknown material is one of the substances listed in the table below.
|
Substance |
Density (g/cm3) |
|---|---|
|
Polyvinylchloride (PVC) |
1.35 |
|
Maple |
0.77 |
|
Acrylic |
1.16 |
|
Polytetrafluoroethylene (Teflon) |
2.20 |
|
Polypropylene |
0.90 |
|
Aluminum |
2.71 |
|
Polyurethane |
1.23 |
Pre-laboratory Assignment: The Density of Solids and Liquids
- Circle the correct responses in the following statement:
Density is a physical / chemical property of matter and an intensive /extensive property of matter.
- What devices will you use to measure the mass and the volume of water in Part A of this lab?
- In Part B of this lab you will perform several measurements in order to determine the density of a metal.
- Name this metal:
- Describe the technique you will use to measure the volume of this metal.
- Consider the tabulated data collected by a student for an unknown metal sample. Use this data to calculate the density of the metal (in g/cm3). Show your work clearly.
|
Mass of Empty Beaker |
44.656 g |
|---|---|
|
Mass of Beaker and Metal sample |
124.400 g |
|
Initial volume of water in cylinder |
12.7 mL |
|
Final volume of water and Metal sample |
21.6 mL |
- In Part C of this lab, you will measure the mass, height and diameter of four cylinders composed of some unknown material.
- Calculate the volume (in cm3) of a cylinder with a measured height of 11.76 cm and a diameter of 7.22 cm. Show your work clearly.
- Each pair of mass and volume values (for each cylinder) will be plotted on a scatter plot, with mass on the y- axis and volume on the x-axis. A best-fit line will then be applied to the plotted data.
- How will you calculate the value of the slope of this best-fit line?
- How will the value of the slope help you identify the unknown material that the cylinders are made of?
Lab Report: The Density of Liquids and Solids
Part A: The Density of Water
Experimental Data
|
1st Water Addition |
2nd Water Addition |
3rd Water Addition |
|
|
Mass of Empty Cylinder |
|||
|
Mass of Cylinder + Water |
|||
|
Mass of Water only |
|||
|
Volume of Water |
|||
|
Density of Water |
|||
|
Average Density of Water |
|||
Temperature of Water: ______________
Data Analysis
- Look up the true density of water at the temperature recorded:_____________
- Obtain this value from http://jupiter.plymouth.edu/~jsdunca...ityOfWater-vs- Temp.pdf. Then use this to calculate the percent error in your average density of water. Show your work.
Part B: The Density of Aluminum and the Thickness of Foil
Experimental Data
Table 1 – The Density of Aluminum
|
Mass of Empty Beaker |
|
|---|---|
|
Mass of Beaker and Al pellets |
|
|
Mass of Al pellets |
|
|
Initial volume of water in cylinder |
|
|
Final volume of water and Al pellets |
|
|
Volume of Al pellets |
Table 2 – The Thickness of Aluminum Foil
|
Mass of Al Foil |
|
|---|---|
|
Length of Al Foil |
|
|
Width of Al Foil |
Data Analysis
- Use your measured mass and volume of the pellets (in Table 1) to calculate the density of aluminum, in g/cm3. Show your work, and report your answer to the correct number of significant figures.
- Look up the true density of aluminum at http://www.chemicool.com: _______________
- Use this to calculate the percent error in your experimentally determined density value. Show your work.
- Use your measurements for the aluminum foil (in Table 2) along with the true density of aluminum to calculate the foil thickness, in cm. Show your work, and report your answer in scientific notation. Consider the foil to be a very flat rectangular box, where: \(\text{Volume of foil}= length \times width \times thickness\)
Part C: Graphical Analysis of Mass and Volume Data of an Unknown Solid
Experimental Data
ID Code of Unknown Solid:
|
Small Cylinder |
Medium Cylinder |
Large Cylinder |
EX Large Cylinder | |
|---|---|---|---|---|
|
Mass |
||||
|
Length |
||||
|
Diameter |
||||
|
Calculated Volume |
Show a sample calculation for volume using your measured dimensions for the small cylinder below.
Data Analysis
- On the graph paper supplied, plot “Mass (Y) versus Volume (X)” for all four cylinders measured. Staple your graph to this report form.
Instructions for Graphing Data
- Use a sharpened pencil.
- Use a ruler to draw your axes.
- Choose axis scales that make use of the entire sheet of graph paper.
- Clearly number and label your axes.
- Use “X” symbols for each plotted point.
- Draw a best-fit straight line through your data points using a ruler.
- Give your graph an appropriate title.
- Choose two points on your best-fit line separated far from each other. The points chosen cannot be any of your plotted data points. Circle the two points selected on your graph, and complete the table below.
|
X Value |
Y Value | |
|---|---|---|
|
Point 1 |
||
|
Point 2 |
Now calculate the slope (\(m\)) of your best-fit line using the equation: \(m = \frac{y_2-y_1}{x_2-x_1}\). Show your work, and report your result to the correct number of significant figures.
- The value of the slope obtained above in #2 yields the density of your unknown solid, in units of g/cm3. Using this value, identify your unknown solid (see Procedure, Part C, #5).
- ID Code of Unknown:
- Name of Unknown:
- True Density:
- You are supplied with another cylinder made of the same material. If the cylinder length is 1.83 feet, calculate the mass of this cylinder, in grams. Use the true density of the solid in this calculation, and assume that the cylinder diameter is the same as all the other cylinders you measured. Show your work.