2.4B: Limiting Reactants and Percent Yield

Limiting Reactants

Let's begin this section with a quick review of stoichiometric ideas in the context of a straightforward problem: the extraction of oxygen out of the air to keep your fingers cozy.

Example 

Problem 2-21) Commercial hand-warmers typically contain finely divided iron in a pouch that is permeable to air and moisture. The pouch is kept in an airtight plastic sleeve which, upon opening, exposes the iron filings to the atmosphere. Heat is soon released as the iron reacts to form hydrated iron oxide, or rust. A simplified version of the reaction is described by the unbalanced equation below.\[ \text{_____}\ \ce{Fe} + \text{_____}\ \ce{O2}\ \ce{->}\   \text{_____}\ \ce{Fe2O3} \nonumber \]

Balance the above equation and then calculate the mass of Fe₂O₃ that would result from the complete reaction of 25.0 g of iron. What mass of oxygen would be consumed in the reaction?

Solution

The balanced equation is:

\[ \ce{2 Fe + 3/2 O2  ->  Fe2O3} \nonumber \]

Note that although we cannot have three-halves of an O₂ molecule, we can have three-halves of a mole of O₂ molecules; as stated earlier, fractional coefficients in chemical equations are nothing to be disturbed by and are, in fact, commonly used.

Using the balanced equation, we can proceed with the stoichiometric aspects of the problem, outlined below.

\[mass_{\ce{Fe2O3}} = 25.0\ g\ \ce{Fe} (\dfrac{1\  mol\ \ce{Fe}}{55.845\ g\ \ce{Fe}})\ (\dfrac{1\ mol\ \ce{Fe2O3}}{2\ mol\  \ce{Fe}})(\dfrac{159.69\ g\  \ce{Fe2O3}}{1\ mol\ \ce{Fe2O3}}) = 35.7\ g\ \ce{Fe2O3} \nonumber \]  

\[mass_{\ce{O2}} = 25.0\ g\ \ce{Fe} (\dfrac{1\  mol\ \ce{Fe}}{55.845\ g\ \ce{Fe}})\ (\dfrac{\frac{3}{2}\ mol\ \ce{O2}}{2\ mol\  \ce{Fe}})(\dfrac{32.00\ g\  \ce{O2}}{1\ mol\ \ce{O2}}) = 10.7\ g\ \ce{O2} \nonumber \]   

---

Image Credit: photo by avlxyz and licensed under CC BY-NC-SA 2.0.

 

Although it is not explicitly stated, the scenario described in Problem 2-21 is similar to the way many chemical reactions are performed in the lab. How so? Although only 10.7 grams of oxygen were actually incorporated into the product, the amount available was much, much greater - in theory all the oxygen in the Earth’s atmosphere had the potential to react with the iron. But the reaction was complete long before our planet’s oxygen was exhausted, thankfully. In other words, the reaction was complete when one of the reactants - the iron - was used completely and, for this reason, the iron is referred to as the limiting reactant, that is, the one that limits the amount of product that can be formed.

In the preparation of compounds, it is rare for the reactants to be combined in exact stoichiometric amounts; usually one or more of them is present in considerable excess, usually for convenience or cost. For example, consider the preparation of cisplatin, an effective chemotherapy agent; the following reaction is performed in one step using potassium iodide, KI, and a platinum-containing compound called potassium tetrachloroplatinate, K₂PtCl₄:

\[ \ce{4 KI + K2PtCl4->  4 KCl + K2PtI4} \nonumber \] 

As you might expect, the platinum-containing reactant is considerably more expensive than potassium iodide (one chemical retailer recently listed K₂PtCl₄ for almost $100 per gram, compared to only 40¢ per gram for KI). Thus, to ensure as complete a conversion as possible of the more expensive material, an excess of the cheaper one is used. 

To illustrate how stoichiometric relationships can help in the design of such synthetic methods, consider the following. Let’s assume that we wanted to perform the reaction above using a five-fold excess of KI, that is, five times the amount required to completely react with the K₂PtCl₄. If we started with 100.0 mg of K₂PtCl₄, we can find stoichiometric amount of KI as follows:

\[ stoichiometric\ mass_{\ce{KI}} = (100\ mg\ \ce{K2PtCl4})(\dfrac {1\ g}{1000\ mg})(\dfrac {1\ mol\ \ce{K2PtCl4}}{415.09\ g\ \ce{K2PtCl4}}) (\dfrac{4\ mol\ \ce{KI}}{1\ mol\ \ce{K2PtCl4}})(\dfrac{166.0\ g\ \ce{KI}}{1\ mol\ \ce{KI}}) = 0.160\ g\ \ce{KI} \nonumber \]

So, to perform the reaction with the desired excess of potassium iodide, i.e., a five-fold excess of KI, we would use 0.800 g KI, or five times the amount calculated above. 

At times we are confronted with scenarios where, given the masses of various reactants, the limiting reactant is not obvious. In such a case, simply use the respective molar masses and stoichiometric ratios to calculate the maximum amount of product that is obtainable from each reactant, one at a time; the reactant that yields the lesser amount of product will be the first to be completely consumed and therefore limits the amount of product that can be generated. Example Problem 2-22  illustrates this idea below.

Example 

Problem 2-22) Aspirin, which is the common name for acetylsalicylic acid, C₉H₈O₄, can be conveniently prepared by the reaction of salicylic acid, C₇H₆O₃, with acetic anhydride, C₄H₆O₃, according to the equation below and illustrated in the following figure:

\[ \ce{C7H6O3 + C4H6O3   ->   C9H8O4 + C2H4O2} \nonumber \]

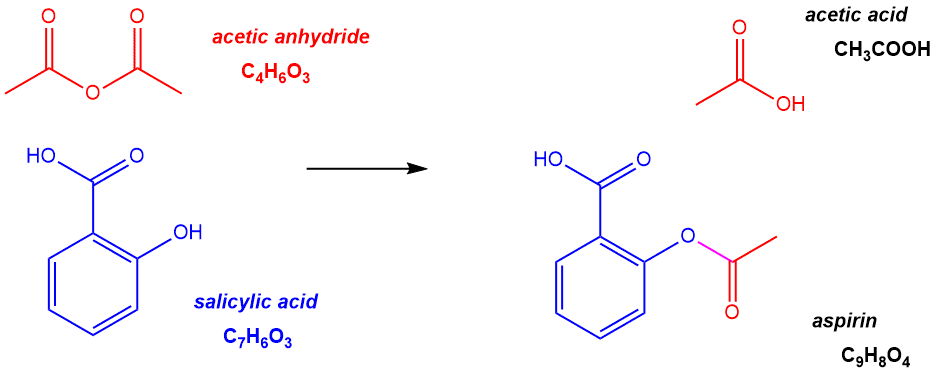
Figure 2.8: Aspirin (also known as acetylsalicyclic acid) is synthesized by reacting acetic anhydride with salicylic acid.

 

Calculate the maximum mass of aspirin, in grams, that can be produced if 50.0 grams of salicylic acid (a solid) reacts with 35.0 mL acetic anhydride (a liquid; density = 1.08 g/mL).

Solution

To determine the maximum amount of aspirin that can be produced, examine each of the reactants in turn, as follows. Beginning with salicylic acid, we find:

\[ mass\ aspirin\ = (50.0\ g\ \ce{C7H6O3})(\dfrac{1\ mol\ \ce{C7H6O3}}{138.1\ g\ \ce{C7H6O3}})(\dfrac{1\ mol\ \ce{C9H8O4}}{1\ mol\ \ce{C7H6O3}})(\dfrac{180.16\ g\ \ce{C9H8O4}}{1\ mol\ \ce{C9H8O4}}) = 65.2\ g\ \ce{C9H8O4} \nonumber \]

A similar calculation is performed for acetic anhydride, albeit with the additional step to determine its mass using the density provided.

 

\[ mass\ aspirin\ = (35.0\ mL\ \ce{C4H6O})(\dfrac{1.08\ g\ \ce{C4H6O}}{1\ mL\ \ce{C4H6O}})(\dfrac{1\ mol\ \ce{C4H6O}}{102.09\ g\ \ce{C4H6O}})(\dfrac{1\ mol\ \ce{C9H8O4}}{1\ mol\ \ce{C4H6O}})(\dfrac{180.16\ g\ \ce{C9H8O4}}{1\ mol\ \ce{C9H8O4}}) = 66.7\ g\ \ce{C9H8O4} \nonumber \]

 

From the above calculations we see that the maximum mass of aspirin that can be made under the stated conditions is 65.2 g. This is because, at the point in the reaction at which that specific mass of product is generated, the salicylic acid is exhausted completely; there is none left to react with the remaining acetic anhydride.

Follow-up exercise: what is the mass of the unreacted acetic anhydride in the above problem?

 

 

 

 

Image Credit: "Vintage Aspirin" by LarsSchwarz is licensed under CC BY-NC-SA 2.0.

 

Percent Yield

A concept related to those above is that of percent yield. The observant reader may have noticed in the above section we refer to the maximum obtainable amount of product from a reaction and not simply the “expected” amount. This phrasing is deliberate because it is rare that a reaction proceeds as straightforwardly as its balanced equation may imply: there are often secondary products, unwanted side-reactions involving impurities in the solvents, etc. Moreover, even for those reactions that do go smoothly, isolating and purifying products can be challenging and can result in considerable “loss” of product. As such, the efficiency of a synthesis is often characterized by the amount of product that is actually obtained expressed as a percentage of that theoretically possible.

This idea is quantified using percent yield. It's a fairly intuitive idea in which the actual mass of product is expressed as a percentage of the maximum mass possible as calculated by stoichiometric considerations.

\[ \%\ \text{yield} = \dfrac{\text{actual mass of product}}{\text{maximum mass possible}}\times 100\% \]

 

Example 

Problem 2-23) Referring to Problem 2-22, calculate the percent yield if 58.3 g of aspirin is obtained when 50.0 grams of salicylic acid (a solid) reacts with 35.0 mL acetic anhydride.

Solution

Using the stoichiometric amount of aspirin calculated above, we find the percent yield as follows:

\[ \%\ \text{yield} = \dfrac{\text{actual mass of product}}{\text{maximum mass possible}}\times 100\% = \dfrac{58.3\ g}{65.2\ g}\times 100\% = 89.4 \% \nonumber \]

 

Exercise

Problem 2-24) As we saw in Chapter 1, alkenes can be converted to alcohols via an addition reaction with water. One example is shown below involving cyclohexene, a liquid alkene with a density of 0.81 g/mL; reaction with water yield the alcohol, cyclohexanol.

If you treat 24.3 mL of cyclohexene with excess water and collect 15.3 g of cyclohexanol, what is the percent yield of the reaction?

Answer

63.7% yield