2.3: Liquid Matters: Density and Concentration

Figure 2-5. For convenience, liquids are usually dispensed, measured and/or sold by volume, not mass. These one gallon cans contain acetone, a commonly used solvent and paint-thinner and the major component of many brands of nail-polish remover. (Photo credit: "Acetone" by pheezy is licensed under CC BY 2.0.)

 

 

There are many occasions in experimental work where it is more convenient to determine the amount of a material by measuring its volume rather than its mass, particularly if the substance is a liquid. Liquids can be either pure materials or mixtures, the difference being the types of particles that make up the material: pure materials consist of only one type of molecule, whereas mixtures are just that, mixtures of more than one type of molecule, sometimes many more. For example, pure water consists only of water molecules, the acetone sold commercially shown at left (ideally) consists only of acetone molecules, C₃H₆O, and pure linoleic acid consists only of linoleic acid molecules. In contrast, most liquids you encounter in day-to-day activities are mixtures: milk, gasoline, coffee, wine, orange juice, blood, etc., all consist of multiple types of molecules that are mixed together. The approach you need to take to determine the amount of material in a liquid, meaning the number of moles of a particular compound, depends on whether or not it is a pure compound or a mixture. 

For pure liquids, the number of moles of a substance can be found from its volume via its density, D. The density of an object is simply the ratio of its mass, m, divided by its volume, V (eq. 2.3.1). Water, for example, has a mass of 1.00 grams per milliliter, or 1.00 g/mL. The volume of liquids is typically expressed in milliliters, mL, whereas that of solids is given in cubic centimeters, cm³. However, since one milliliter is defined as one cubic centimeter, the distinction is of little consequence and you can directly compare density values expressed in these units as they are numerically equivalent.

\[ D = \dfrac{m}{V} \]

Examples 

Problem 2-8: A sample of acetone has a volume of 250 mL and a mass of 198 g. What is its density?

Solution

This is a straightforward application of equation 2.3.1.

\[ D = \dfrac{m}{V} = \dfrac{198\ g}{250\ mL} = 0.792 g\  mL^{-1} \nonumber \]

 

The following two problems require you to use the result from problem 2-8 and to rearrange the equation for density.

Problem 2-9: How many moles of acetone, C₃H₆O, are in a 1.00 L sample of the solvent?

Solution. You can first find the mass as shown below. Then, using the molar mass of (58.08 g/mol) you can find the number of moles.

\[ m = DV = (0.792\ g\ \cancel{mL^{-1}})(1.00\ \cancel{L})(\dfrac{1000\ \cancel{mL}}{1\ \cancel{L}}) = 792\ g \nonumber \]

\[ moles_{\ce{C3H6O}} = (792\cancel{g\ \ce{C3H6O}})(\dfrac{1\ mol\ \ce{C3H6O}}{58.08\ \cancel{g\ \ce{C3H6O}}}) = 13.6\ mol\ \ce{C3H6O} \nonumber \]

 

Problem 2-10: A lab procedure requires you to use 2.0 moles of acetone. The easiest way to measure this is using volume, not mass (you don't want to spill flammable liquids on an electric instrument). What volume do you need to use to deliver the required amount of acetone? 

Solution

\[ V = \dfrac{m}{D} = \dfrac{120\ \cancel{g}}{0.660\ \cancel{g}\ mL^{-1}}= 182\ mL \nonumber \]

Exercise 

Problem 2-11. The density of gasoline is roughly 0.75 g/mL. Estimate the weight, in pounds, of 16 gallons of gasoline, a fairly typical tank size for automobiles in the US. (1 gallon = 3.79 L; 1 pound = 454 g)

Example

Problem 2-12. An irregularly shaped piece of metal with a mass of 28.0 g is thought to be tin (D = 7.37 g/cm³). Its volume is determined by placing it in a partially filled graduated cylinder: the volume of the water displaced upon submerging the sample is equal to the volume of the solid. If the volume of the water is 5.1 mL initially and the reading on the graduated cylinder increases to 8.9 mL upon submersion of the metal, what is the density of the object? Is it consistent with that of tin?

Solution

The density is calculated using eq. 2.3.1 as shown below. 

\[D = \dfrac{m}{V} = \dfrac{28.0\ g}{(8.9\ mL - 5.1\ mL)(\dfrac{1\ cm^{3}}{1\ mL})}= 7.4\ g cm^{-3}  \nonumber \]

The density is consistent with that of tin, but one needs to be wary of reading too much into this: the fact that the density matches that of tin does not prove that the metal is, in fact, tin. Different materials can have the similar densities; indium and manganese have densities so close to tin’s that, given the limited precision of the method used, they would give identical results. Additional supporting evidence would be needed to establish the metal’s identity.

 

As mentioned above, a different approach must be taken when calculating the amount of a material in a liquid mixture. Let's pause here to define a few terms, because there are several types of liquid mixtures you will encounter and it will be helpful to know what their characteristics are. We'll begin with the term mixture. To restate its definition, a mixture is any combination of materials that consists of more than one type of fundamental particle: atoms are the fundamental particle of an element and molecules are the fundamental particle for compounds. Beyond that, there are two types of mixtures: homogeneous and heterogeneous. Homogeneous mixtures are those that have the same composition throughout the mixture because the particles are randomized at the molecular level. For example if you have a mixture of two types of particles, A and B, the ratio of A and B is the same no matter where in the sample you look – there are no regions that are richer in A or richer in B. Heterogeneous mixtures, on the other hand, have distinct regions where one type of molecule is prevalent and other areas it is not. A familiar example is oil and water; you can mix oil and water together and stir vigorously, but you will always have droplets that are essentially oil suspended in water; these droplets are composed primarily of oil, whereas the aqueous matrix in which they are suspended is almost exclusively water molecules.

Figure 2-6. Three types of liquids. A glass of water (center) is an example of a pure substance, consisting of only one type of particle. Mixtures contain more than one type of particle and can be either heterogeneous or homogeneous. Heterogenous mixtures (left) either have visibly discernable regions with different compositions (such as the oil and vinegar layers of some salad dressings, bottom left), or appear cloudy or milky (as is the case with milk, top left). Homogeneous mixtures, such a white vinegar (right, top) or sulfuric acid (right, bottom) appear uniform throughout, are free of any cloudiness or opacity.

 

Can you tell the difference between homo- and heterogeneous mixtures by their appearance? Yes. In some cases the different regions are large enough that you can see them with the naked eye, such as oil droplets in water, or a layer of oil floating on top of water. If the particles are small, however, you may not be able to visually discern them as particles, but they interact with light differently than the randomized particles of homogeneous mixtures. Specifically, heterogeneous mixtures are usually cloudy, milky, or opaque. Milk is an excellent example. There are no "white" particles in milk, yet it looks white. Why? It has to do with the way light interacts with the particles of the mixture. Milk (especially whole milk) consists of small (to us) globules of fat that are suspended in an aqueous – meaning water-based – medium. They are too small to see, but they are large enough to "scatter" light by reflecting it from all of the globule surfaces. A beam of light can't pass through milk without the particles changing the scattering the light in all directions. The consequence is that you can't see through it and it appears opaque. Skim milk has fewer fat globules so is not as opaque, but still is distinctly cloudy. Homogeneous mixtures allows light to travel through them in a straight line: this means that they look clear and transparent, without being cloudy or smoky looking. As a result, homogeneous mixtures of colorless compounds in water are visibly indistinguishable from pure water. When you dissolve salt, sugar, or a host of other compounds in water, the result is a clear, colorless liquid mixture that is free of cloudiness or any visible particles. 

Homogeneous mixtures are more often referred to as solutions and we will focus on those as they are much more frequently encountered in lab settings. The sample of white vinegar shown is essentially a 5% solution of acetic acid in water. A few more definitions here. Solutions have two types of components: the solute, which is the compound or compounds that are dissolved in the solvent, which is major component of the solution. Vinegar therefore contains acetic acid as the solute and water serves the solvent. Solutions often contain multiple solutes. Ocean water, for example, contains many different compounds but, provided there is no insoluble debris suspended in it, is a solution.

The amount of solute in a solution is called its concentration. There are a number of different ways to express the concentration of solutions, perhaps the most familiar is as a percent, such as the vinegar example above. Saying that a solution is "5% acetic acid" means that there are 5 grams of acetic acid in 100 grams of the solution. Typical ocean water is about 3.5% sodium chloride, NaCl. But, as was the case with solids, it is the number of particles, not the mass or volume, that is usually important when thinking about the amounts of compounds that will react with each other. For example, if we have equal volumes of two 1% solutions, one of acetic acid (CH₃COOH) and one of formic acid (HCOOH), the number of solute molecules in those solutions will be different despite the fact that the masses of the solutes are the same. We therefore need a way of expressing how many particles of a given solute is in a solution because the mass of the dissolved material does not do so directly. Chemists usually deal with this by expressing the concentration using of solutions using molarity, defined as the moles of solute per liter of solution. By convention, the concentration in molarity of a given compound is often referred to using the formula of the compound within square brackets; thus [HCOOH] means "the molarity of formic acid" in a given context, e.g., when its concentration is 0.500 mol/L (or 0.500 molar), it would be written as [HCOOH] = 0.500 M. 

 

Definition: Term

Molarity: For a  given solute, X, its molarity in a given solution, [X], is defined as the ratio of the moles of X, n_X, to the volume of the solution in litres, V.

\[ [\ce{X}] =  \dfrac{n_{\ce{X}}}{V}  \]

 

To illustrate the concept the problem below uses the just-mentioned solutions of acetic and formic acids as examples: they have the same weight percent, but what are their concentrations when expressed in molarity?

 

Example 

Problem 2-13. Calculate the concentration, in molarity, of the following two solutions; assume the density of both solutions is 1.00 g/mL.*

a) 1% acetic acid (CH₃COOH)
b) 1% formic acid (HCOOH) 

Solution

To calculate the molarity of the solutions we need to first know the masses of the solutes in each, then convert those masses to moles. We can find the mass of the solutes using the density and percent composition as shown below. For simplicity, we'll use 1.00 L as the volume, but that is an arbitrary choice.

\[ mass_{solute} = 1\%\ mass_{solution} = 1\%\ (Vd)_{solution} = (0.01)(1.00 L) (\dfrac{1.00\ g}{mL})(\dfrac{1000 mL}{L})= 10 g\ solute \nonumber \]

Thus 1.00 liters of both solutions each have 10.0 grams of solute: solution (a) has 10.0 grams of acetic acid, and solution (b) has 10.0 grams of formic acid. But the molarities of these solutions are not the same because equal masses don't correspond to equal numbers of particles. The calculation of molarity shown below amounts to a simple unit conversion, where we convert the concentration expressed in terms of grams per liter to moles per liter.

For solution a:

\[[\ce{CH3COOH}] = (\dfrac{10.0\ \cancel{g}\ \ce{CH3COOH}}{1.00\ L})(\dfrac{1\ mol\ \ce{CH3COOH}}{60.03\ \cancel{g}\ \ce{CH3COOH}}) = \dfrac{0.167\ mol\ \ce{CH3COOH}}{L} = 0.167\  M \nonumber \]

 

For solution b:

\[[\ce{HCOOH}] = (\dfrac{10.0\ \cancel{g}\ \ce{HCOOH}}{1.00\ L})(\dfrac{1\ mol\ \ce{HCOOH}}{46.02\ \cancel{g}\ \ce{HCOOH}}) = \dfrac{0.217\ mol\ \ce{HCOOH}}{L} = 0.217 M \nonumber \]

 

* Why do we need to assume a density? We know the mass percent of the solute, but without the total mass of the solution it would not be possible to determine the mass of the solute, which we need to find the number of moles. See question 2-X for an example of a solution that does not have a density of 1.00 g/mL.

 

As we shall see, relating the amounts of reactants to each other using volumes and molarities is the basis for a wide range of analytical techniques.

Exercise 

Problem 2-14. Calculate the molarity of the following aqueous solutions: 

a) 0.050 mol of formic acid in a solution with volume of 0.25 L
b) 20.0 grams of glucose (C₆H₁₂O₆) in a solution with a volume of 100.0 mL
c) 5.0 mL of pure ethanol (density = 0.789 g/mL) dissolved in enough water to make a 500.0 mL solution

Answers

a) [HCOOH] = 0.20 M; b) [C₆H₁₂O₆] = 1.11 M; c) [CH₃CH₂OH] = 0.17 M

 

As we saw with the density equation, it is often necessary to rearrange the terms to solve for a desired quantity. If you know any two of the following three values for a solutions - volume, moles of solute, or molarity, you can find the missing value algebraically. The following example illustrates the point.

Exercise 

Problem 2-15. How many moles of solute are contained in 250.0 mL of a 0.2146 M solution of hydrochloric acid (HCl).

Answer

In this question you are given a volume and a concentration; you can find the number of moles by rearranging the equation for molarity (equation 2.3.2) as shown below. Note how the product of a volume and concentration has units of moles.

\[ n_{X}\ = [X]V \nonumber     \]

\[n_{\ce{HCl}} = [\ce{HCl}]V_{\ce{HCl}}\ = (\dfrac{0.2146\ mol\ \ce{HCl}}{1\ \cancel{L}})(250.0\ \cancel{mL})(\dfrac{1\ \cancel{L}}{1000\ \cancel{mL}})\ = 0.05365 mol \ce{HCl} \nonumber \]

 

Exercise 

Problem 2-16. You are performing an experiment that requires you to add 5.0 grams of dissolved sodium chloride (NaCl) to a beaker. You have a solution that is 1.5 M in NaCl; how many milliliters do you need to add to the beaker to deliver the correct amount of solute? 

Answer

Start by rearranging the equation 2.3.2 to yield an expression for volume, as shown below. In the numerator, use the molar mass of sodium chloride to convert the 5.0 grams you need to deliver to moles. 

\[ V_{\ce{NaCl}\ solution} = \dfrac{n_{\ce{NaCl}}}{[\ce{NaCl}]}\  \nonumber     \]

\[V_{\ce{NaCl}\  solution} = \dfrac{(5.00\ \cancel{g\ \ce{NaCl}})(\dfrac{1\ \cancel{mol\ \ce{NaCl|}}}{58.44 \cancel{g\ \ce{NaCl}}})}{(\dfrac{1.5\ \cancel{mol\ \ce{NaCl}}}{1\ \cancel{L}})(\dfrac{1\ \cancel{L}}{1000\ mL})} = 57\ mL    \nonumber \]

 

---

Additional Problems.

Problem 2-17. The CRC Handbook of Chemistry and Physics is a treasure trove of useful and interesting information. A copy of this shoebox-sized book sits on the bookshelves of most chemists (at least those who were in college before the internet!). The following graph was prepared from one table of data in the CRC and shows the density of saline solutions as a function of the weight percent of sodium chloride. As you can see, the data is nearly linear and is closely approximated by the following equation:

\[ D = (7.6×10^{-3}\dfrac{(\dfrac{g}{mL})}{Wt\ \%})(Wt.\  \%) + 0.997\ \dfrac{g}{mL} \nonumber \]

 

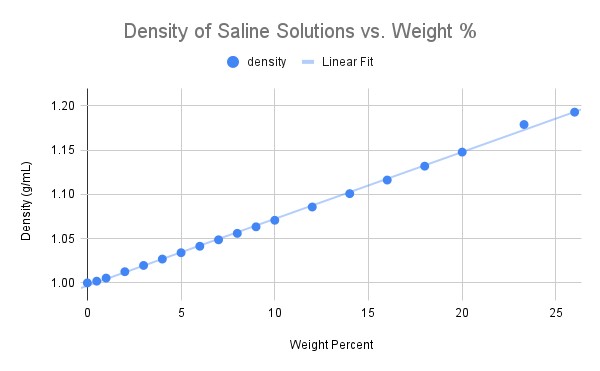
From this information, estimate the molarity of a solution that:

a) has a density of 1.08 g/mL
b) is 19.2% NaCl by weight