9.3: Covalent Bonding
- Page ID
- 98642
Skills to Develop
- Describe the formation of covalent bonds
- Define electronegativity and assess the polarity of covalent bonds
In ionic compounds, electrons are transferred between atoms of different elements to form ions. But this is not the only way that compounds can be formed. Atoms can also make chemical bonds by sharing electrons between each other. Such bonds are called covalent bonds. Covalent bonds are formed between two atoms when both have similar tendencies to attract electrons to themselves (i.e., when both atoms have identical or fairly similar ionization energies and electron affinities). For example, two hydrogen atoms bond covalently to form an H2 molecule; each hydrogen atom in the H2 molecule has two electrons stabilizing it, giving each atom the same number of valence electrons as the noble gas He.
Compounds that contain covalent bonds exhibit different physical properties than ionic compounds. Because the attraction between molecules, which are electrically neutral, is weaker than that between electrically charged ions, covalent compounds generally have much lower melting and boiling points than ionic compounds. In fact, many covalent compounds are liquids or gases at room temperature, and, in their solid states, they are typically much softer than ionic solids. Furthermore, whereas ionic compounds are good conductors of electricity when dissolved in water, most covalent compounds, being electrically neutral, are poor conductors of electricity in any state.
Formation of Covalent Bonds
Nonmetal atoms frequently form covalent bonds with other nonmetal atoms. For example, the hydrogen molecule, H2, contains a covalent bond between its two hydrogen atoms. Figure \(\PageIndex{1}\) illustrates why this bond is formed. Starting on the far right, we have two separate hydrogen atoms with a particular potential energy, indicated by the red line. Along the x-axis is the distance between the two atoms. As the two atoms approach each other (moving left along the x-axis), their valence orbitals (1s) begin to overlap. The single electrons on each hydrogen atom then interact with both atomic nuclei, occupying the space around both atoms. The strong attraction of each shared electron to both nuclei stabilizes the system, and the potential energy decreases as the bond distance decreases. If the atoms continue to approach each other, the positive charges in the two nuclei begin to repel each other, and the potential energy increases. The bond length is determined by the distance at which the lowest potential energy is achieved.
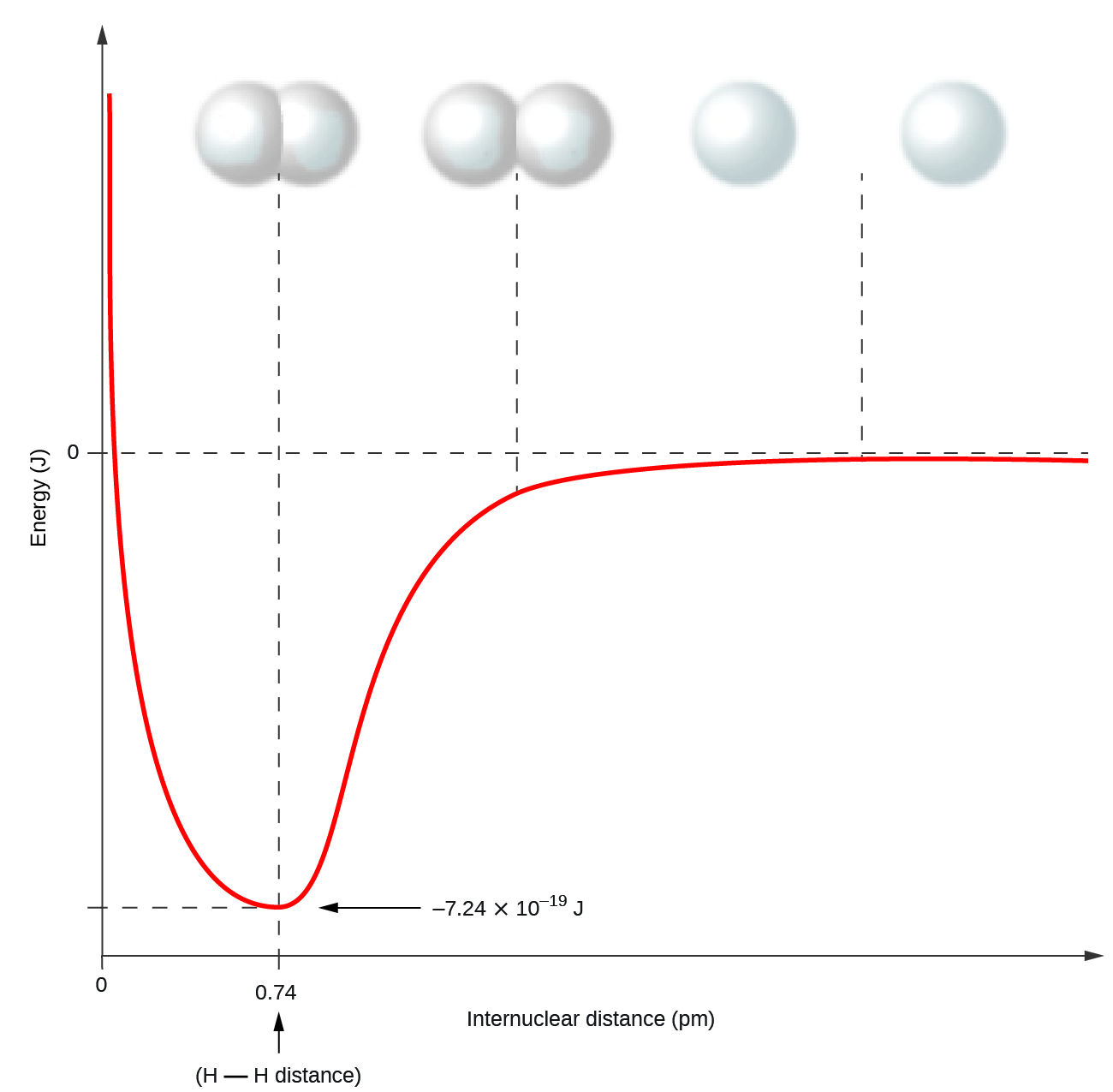
Figure \(\PageIndex{1}\): The potential energy of two separate hydrogen atoms (right) decreases as they approach each other, and the single electrons on each atom are shared to form a covalent bond. The bond length is the internuclear distance at which the lowest potential energy is achieved.
It is essential to remember that energy must be added to break chemical bonds (an endothermic process), whereas forming chemical bonds releases energy (an exothermic process). In the case of H2, the covalent bond is very strong; a large amount of energy, 436 kJ, must be added to break the bonds in one mole of hydrogen molecules and cause the atoms to separate:
\[\ce{H2}(g)⟶\ce{2H}(g)\hspace{20px}ΔH=\mathrm{436\:kJ}\]
Conversely, the same amount of energy is released when one mole of H2 molecules forms from two moles of H atoms:
\[\ce{2H}(g)⟶\ce{H2}(g)\hspace{20px}ΔH=\mathrm{−436\:kJ}\]
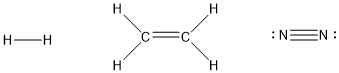
The H2 molecule is described as having a single bond – that is, a covalent bond consisting of one shared pair of electrons. However, in covalent molecules, two atoms may share more than one pair of electrons between them, forming multiple bonds. For example, in the ethylene molecule (C2H4), the carbon atoms share two electron pairs, forming a double bond. In the dinitrogen molecule (N2), the nitrogen atoms share three electron pairs, forming a triple bond. The more electron pairs are shared between two atoms, the stronger the bond will be (i.e. the more energy will be required to break it). In the structures below, multiple bonds are indicated by double or triple lines between the atoms:
Pure vs. Polar Covalent Bonds
If the atoms that form a covalent bond are identical, as in H2, Cl2, and other diatomic molecules, then the electrons in the bond must be shared equally. We refer to this as a pure covalent bond. Electrons shared in pure covalent bonds have an equal probability of being near each nucleus. In the case of Cl2, each atom starts off with seven valence electrons, and each Cl shares one electron with the other, forming one covalent bond:
\[\ce{Cl + Cl⟶Cl2}\]
The total number of electrons around each individual atom consists of six nonbonding electrons and two shared (i.e., bonding) electrons for eight total electrons, matching the number of valence electrons in the noble gas argon. Since the bonding atoms are identical, Cl2 also features a pure covalent bond.
When the atoms linked by a covalent bond are different, the bonding electrons are shared, but no longer equally. Instead, the bonding electrons are more attracted to one atom than the other, giving rise to a shift of electron density toward that atom. This unequal distribution of electrons is known as a polar covalent bond, characterized by a partial positive charge on one atom and a partial negative charge on the other. The atom that attracts the electrons more strongly acquires the partial negative charge and vice versa. For example, the electrons in the H–Cl bond of a hydrogen chloride molecule spend more time near the chlorine atom than near the hydrogen atom. Thus, in an HCl molecule, the chlorine atom carries a partial negative charge and the hydrogen atom has a partial positive charge. Figure \(\PageIndex{2}\) shows the distribution of electrons in the H–Cl bond. Note that the shaded area around Cl is much larger than it is around H. Compare this to Figure \(\PageIndex{1}\), which shows the even distribution of electrons in the H2 nonpolar bond. We sometimes designate the positive and negative atoms in a polar covalent bond using a lowercase Greek letter “delta,” δ, with a plus sign or minus sign to indicate whether the atom has a partial positive charge (δ+) or a partial negative charge (δ–). This symbolism is shown for the H–Cl molecule in Figure \(\PageIndex{2b}\).
Figure \(\PageIndex{2}\): (a) The distribution of electron density in the HCl molecule is uneven. The electron density is greater around the chlorine nucleus. The small, black dots indicate the location of the hydrogen and chlorine nuclei in the molecule. (b) Symbols δ+ and δ– indicate the polarity of the H–Cl bond.
Electronegativity and Polarity
The polarity of a bond—the extent to which it is polar—is determined largely by the relative electronegativities of the bonded atoms. Electronegativity (χ) was defined as the ability of an atom in a molecule or an ion to attract electrons to itself. Thus there is a direct correlation between electronegativity and bond polarity. A bond is nonpolar if the bonded atoms have equal electronegativities. If the electronegativities of the bonded atoms are not equal, however, the bond is polarized toward the more electronegative atom. A bond in which the electronegativity of B (χB) is greater than the electronegativity of A (χA), for example, is indicated with the partial negative charge on the more electronegative atom:
\[ \begin{matrix}
_{less\; electronegative}& & _{more\; electronegative}\\
A\; \; &-& B\; \; \; \; \\
^{\delta ^{+}} & & ^{\delta ^{-}}
\end{matrix} \label{9.3.1} \]
One way of estimating the ionic character of a bond—that is, the magnitude of the charge separation in a polar covalent bond—is to calculate the difference in electronegativity between the two atoms: Δχ = χB − χA.
To predict the polarity of the bonds in Cl2, HCl, and NaCl, for example, we look at the electronegativities of the relevant atoms: χCl = 3.16, χH = 2.20, and χNa = 0.93. Cl2 must be nonpolar because the electronegativity difference (Δχ) is zero; hence the two chlorine atoms share the bonding electrons equally. In NaCl, Δχ is 2.23. This high value is typical of an ionic compound (Δχ ≥ ≈1.5) and means that the valence electron of sodium has been completely transferred to chlorine to form Na+ and Cl− ions. In HCl, however, Δχ is only 0.96. The bonding electrons are more strongly attracted to the more electronegative chlorine atom, and so the charge distribution is
\[ \begin{matrix}
_{\delta ^{+}}& & _{\delta ^{-}}\\
H\; \; &-& Cl
\end{matrix} \]
Remember that electronegativities are difficult to measure precisely and different definitions produce slightly different numbers. In practice, the polarity of a bond is usually estimated rather than calculated.
Bond polarity and ionic character increase with an increasing difference in electronegativity.
As with bond energies, the electronegativity of an atom depends to some extent on its chemical environment. It is therefore unlikely that the reported electronegativities of a chlorine atom in NaCl, Cl2, ClF5, and HClO4 would be exactly the same.
Electronegativity and Bond Type
The absolute value of the difference in electronegativity (ΔEN) of two bonded atoms provides a rough measure of the polarity to be expected in the bond and, thus, the bond type. When the difference is very small or zero, the bond is covalent and nonpolar. When it is large, the bond is polar covalent or ionic. The absolute values of the electronegativity differences between the atoms in the bonds H–H, H–Cl, and Na–Cl are 0 (nonpolar), 0.9 (polar covalent), and 2.1 (ionic), respectively. The degree to which electrons are shared between atoms varies from completely equal (pure covalent bonding) to not at all (ionic bonding), as shown in Figure \(\PageIndex{3}\).
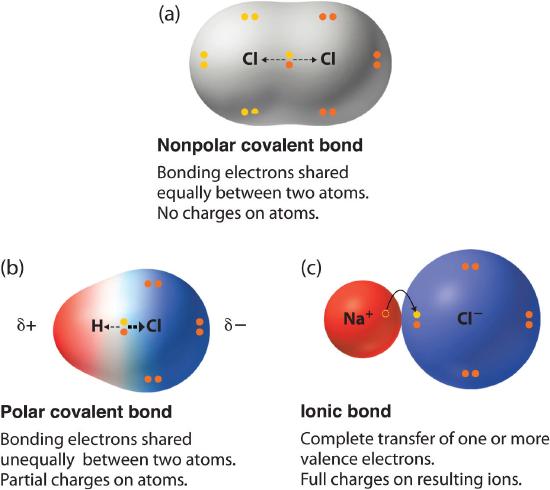
Figure \(\PageIndex{3}\): The Electron Distribution in a Nonpolar Covalent Bond, a Polar Covalent Bond, and an Ionic Bond Using Lewis Electron Structures. In a purely covalent bond (a), the bonding electrons are shared equally between the atoms. In a purely ionic bond (c), an electron has been transferred completely from one atom to the other. A polar covalent bond (b) is intermediate between the two extremes: the bonding electrons are shared unequally between the two atoms, and the electron distribution is asymmetrical with the electron density being greater around the more electronegative atom. Electron-rich (negatively charged) regions are shown in blue; electron-poor (positively charged) regions are shown in red.
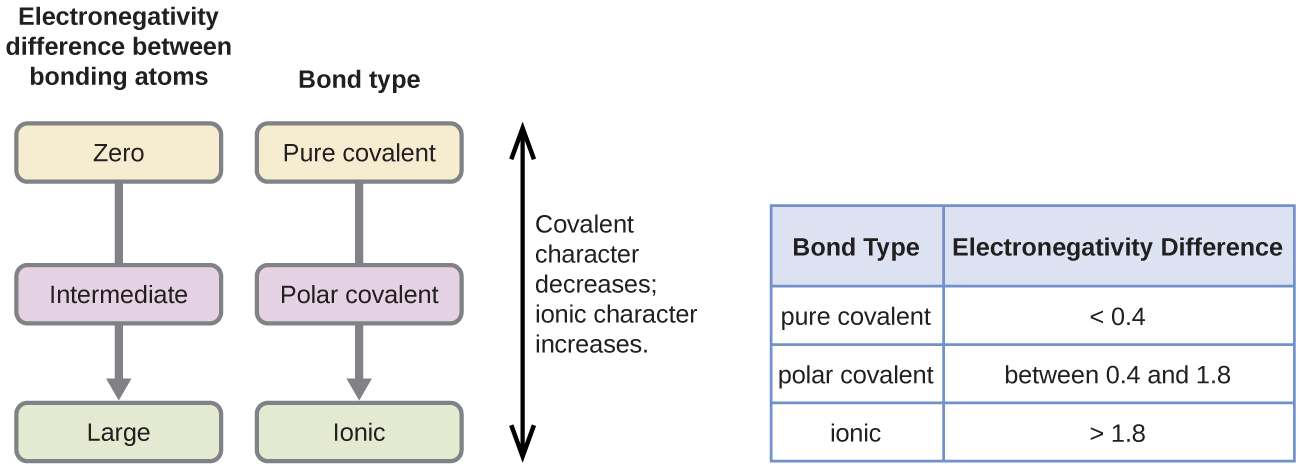
Figure \(\PageIndex{4}\): As the electronegativity difference increases between two atoms, the bond becomes more ionic.
A rough approximation of the electronegativity differences associated with covalent, polar covalent, and ionic bonds is shown in Figure \(\PageIndex{4}\). This table is just a general guide, however, with many exceptions. For example, the H and F atoms in HF have an electronegativity difference of 1.9, and the N and H atoms in NH3 a difference of 0.9, yet both of these compounds form bonds that are considered polar covalent. Likewise, the Na and Cl atoms in NaCl have an electronegativity difference of 2.1, and the Mn and I atoms in MnI2 have a difference of 1.0, yet both of these substances form ionic compounds.
The best guide to the covalent or ionic character of a bond is to consider the types of atoms involved and their relative positions in the periodic table. Bonds between two nonmetals are generally covalent; bonding between a metal and a nonmetal is often ionic.
Some compounds contain both covalent and ionic bonds. The atoms in polyatomic ions, such as OH–,
Example \(\PageIndex{1}\): Electronegativity and Bond Polarity
Bond polarities play an important role in determining the structure of proteins. Using the electronegativity values in Table A2, arrange the following covalent bonds—all commonly found in amino acids—in order of increasing polarity. Then designate the positive and negative atoms using the symbols δ+ and δ–:
C–H, C–N, C–O, N–H, O–H, S–H
Solution
The polarity of these bonds increases as the absolute value of the electronegativity difference increases. The atom with the δ– designation is the more electronegative of the two. Table \(\PageIndex{1}\) shows these bonds in order of increasing polarity.
| Bond | ΔEN | Polarity |
|---|---|---|
| C–H | 0.4 | \(\overset{δ−}{\ce C}−\overset{δ+}{\ce H}\) |
| S–H | 0.4 | \(\overset{δ−}{\ce S}−\overset{δ+}{\ce H}\) |
| C–N | 0.5 | \(\overset{δ+}{\ce C}−\overset{δ−}{\ce N}\) |
| N–H | 0.9 | \(\overset{δ−}{\ce N}−\overset{δ+}{\ce H}\) |
| C–O | 1.0 | \(\overset{δ+}{\ce C}−\overset{δ−}{\ce O}\) |
| O–H | 1.4 | \(\overset{δ−}{\ce O}−\overset{δ+}{\ce H}\) |
Exercise \(\PageIndex{1}\)
Silicones are polymeric compounds containing, among others, the following types of covalent bonds: Si–O, Si–C, C–H, and C–C. Using the electronegativity values in Figure \(\PageIndex{3}\), arrange the bonds in order of increasing polarity and designate the positive and negative atoms using the symbols δ+ and δ–.
Answer
| Bond | Electronegativity Difference | Polarity |
|---|---|---|
| C–C | 0.0 | nonpolar |
| C–H | 0.4 | \(\overset{δ−}{\ce C}−\overset{δ+}{\ce H}\) |
| Si–C | 0.7 | \(\overset{δ+}{\ce{Si}}−\overset{δ−}{\ce C}\) |
| Si–O | 1.7 | \(\overset{δ+}{\ce{Si}}−\overset{δ−}{\ce O}\) |
Dipole Moments and Percent Ionic Character
Although we can estimate the polarity of a bond using electronegativities, the polarity of molecules can also be measured experimentally. The asymmetrical charge distribution in a polar substance such as HCl produces a dipole moment, abbreviated by the Greek letter mu (µ). The dipole moment is defined as the product of the partial charge Q on the bonded atoms and the distance r between the partial charges:
\[ \mu=Qr \label{9.3.2} \]
where Q is measured in coulombs (C) and r in meters. The unit for dipole moments is the debye (D):
\[ 1\; D = 3.3356\times 10^{-30}\; C\cdot ·m \label{9.3.3} \]
When a molecule with a dipole moment is placed in an electric field, it tends to orient itself with the electric field because of its asymmetrical charge distribution (Figure \(\PageIndex{5}\)).
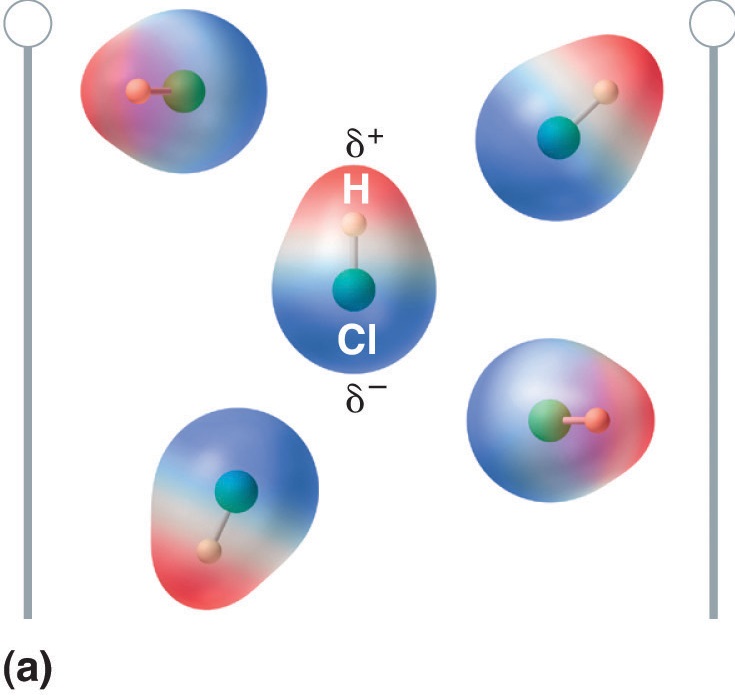
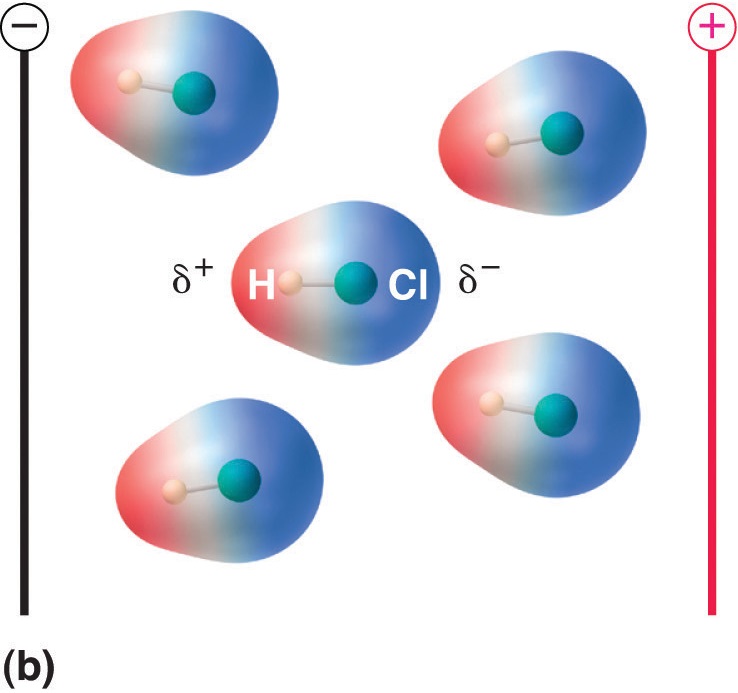
Figure \(\PageIndex{5}\): Molecules That Possess a Dipole Moment Partially Align Themselves with an Applied Electric Field. In the absence of a field (a), the HCl molecules are randomly oriented. When an electric field is applied (b), the molecules tend to align themselves with the field, such that the positive end of the molecular dipole points toward the negative terminal and vice versa.
We can measure the partial charges on the atoms in a molecule such as HCl using Equation \(\ref{9.3.2}\). If the bonding in HCl were purely ionic, an electron would be transferred from H to Cl, so there would be a full +1 charge on the H atom and a full −1 charge on the Cl atom. The dipole moment of HCl is 1.109 D, as determined by measuring the extent of its alignment in an electric field, and the reported gas-phase H–Cl distance is 127.5 pm. Hence the charge on each atom is
\[ Q=\dfrac{\mu }{r} =1.109\;\cancel{D}\left ( \dfrac{3.3356\times 10^{-30}\; C\cdot \cancel{m}}{1\; \cancel{D}} \right )\left ( \dfrac{1}{127.8\; \cancel{pm}} \right )\left ( \dfrac{1\; \cancel{pm}}{10^{-12\;} \cancel{m}} \right )=2.901\times 10^{-20}\;C \label{9.3.4} \]
By dividing this calculated value by the charge on a single electron (1.6022 × 10−19 C), we find that the electron distribution in HCl is asymmetric and that effectively it appears that there is a net negative charge on the Cl of about −0.18, effectively corresponding to about 0.18 e−. This certainly does not mean that there is a fraction of an electron on the Cl atom, but that the distribution of electron probability favors the Cl atom side of the molecule by about this amount.
\[ \dfrac{2.901\times 10^{-20}\; \cancel{C}}{1.6022\times 10^{-19}\; \cancel{C}}=0.1811\;e^{-} \label{9.3.5} \]
To form a neutral compound, the charge on the H atom must be equal but opposite. Thus the measured dipole moment of HCl indicates that the H–Cl bond has approximately 18% ionic character (0.1811 × 100), or 82% covalent character. Instead of writing HCl as
\[ \begin{matrix}
_{\delta ^{+}}& & _{\delta ^{-}}\\
H\; \; &-& Cl
\end{matrix} \]
we can therefore indicate the charge separation quantitatively as
\[ \begin{matrix}
_{0.18\delta ^{+}}& & _{0.18\delta ^{-}}\\
H\; \; &-& Cl
\end{matrix} \]
Our calculated results are in agreement with the electronegativity difference between hydrogen and chlorine χH = 2.20; χCl = 3.16, χCl − χH = 0.96), a value well within the range for polar covalent bonds. We indicate the dipole moment by writing an arrow above the molecule. Mathematically, dipole moments are vectors, and they possess both a magnitude and a direction. The dipole moment of a molecule is the vector sum of the dipoles of the individual bonds. In HCl, for example, the dipole moment is indicated as follows:
The arrow shows the direction of electron flow by pointing toward the more electronegative atom.
The charge on the atoms of many substances in the gas phase can be calculated using measured dipole moments and bond distances. Figure \(\PageIndex{6}\) shows a plot of the percent ionic character versus the difference in electronegativity of the bonded atoms for several substances. According to the graph, the bonding in species such as NaCl(g) and CsF(g) is substantially less than 100% ionic in character. As the gas condenses into a solid, however, dipole–dipole interactions between polarized species increase the charge separations. In the crystal, therefore, an electron is transferred from the metal to the nonmetal, and these substances behave like classic ionic compounds. The data in Figure \(\PageIndex{6}\) show that diatomic species with an electronegativity difference of less than 1.5 are less than 50% ionic in character, which is consistent with our earlier description of these species as containing polar covalent bonds.
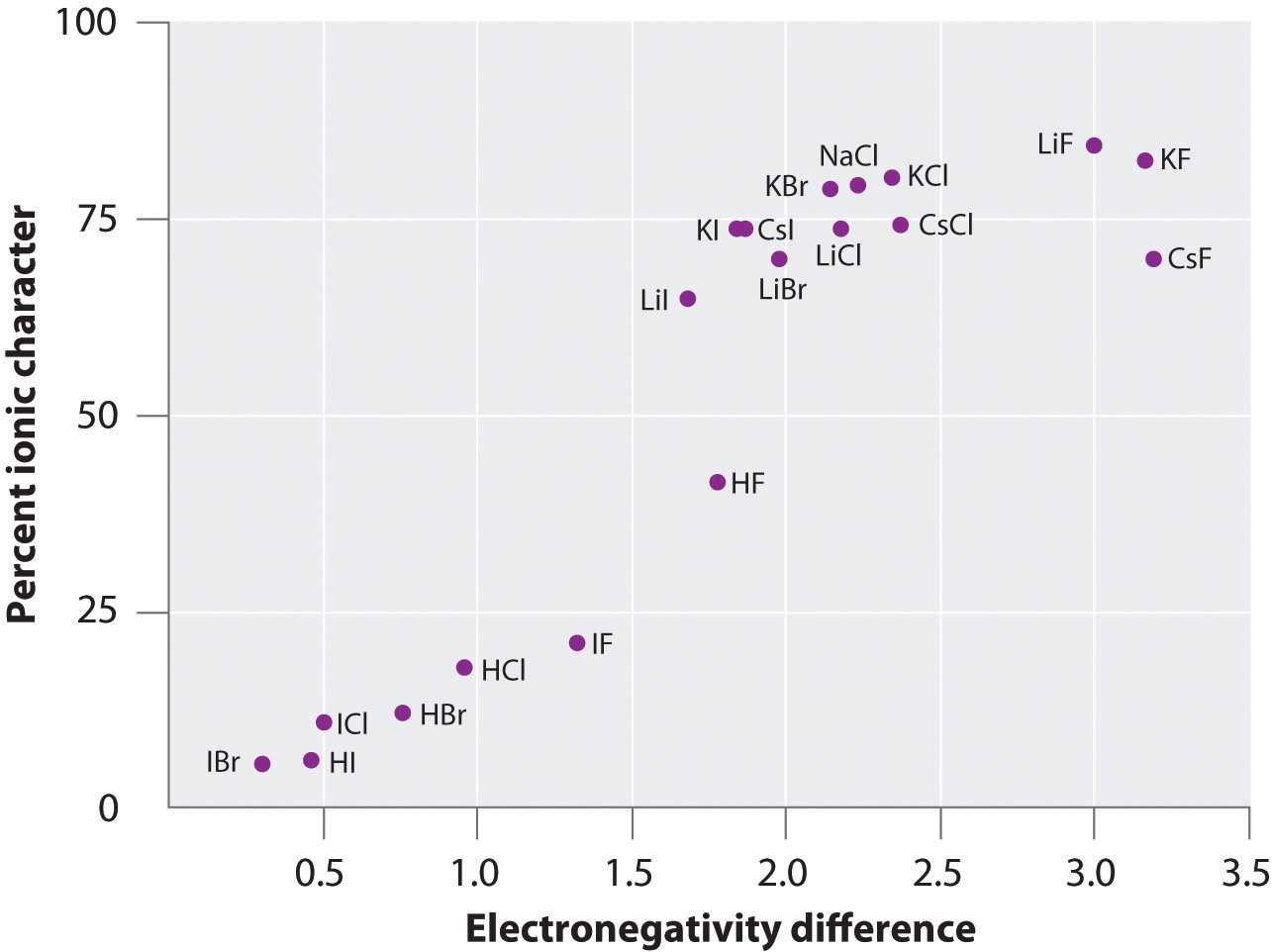
Figure \(\PageIndex{6}\): A Plot of the Percent Ionic Character of a Bond as Determined from Measured Dipole Moments versus the Difference in Electronegativity of the Bonded Atoms.In the gas phase, even CsF, which has the largest possible difference in electronegativity between atoms, is not 100% ionic. Solid CsF, however, is best viewed as 100% ionic because of the additional electrostatic interactions in the lattice.
Summary
Covalent bonds form when electrons are shared between atoms and are attracted by the nuclei of both atoms. The number of electron pairs determine whether a covalent bond is classified as a single, double, or triple bond. In pure covalent bonds, the electrons are shared equally. In polar covalent bonds, the electrons are shared unequally, as one atom exerts a stronger force of attraction on the electrons than the other. The ability of an atom to attract a pair of electrons in a chemical bond is called its electronegativity. The difference in electronegativity between two atoms determines how polar a bond will be. In a diatomic molecule with two identical atoms, there is no difference in electronegativity, so the bond is nonpolar or pure covalent. When the electronegativity difference is very large, as is the case between metals and nonmetals, the bonding is characterized as ionic. The percent ionic character of polar covalent bonds can be calculated by measuring the dipole moment.
Contributors
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Anna Christianson (Bellarmine University)