7.9: Building the Periodic Table
- Page ID
- 98632
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- To correlate the arrangement of atoms in the periodic table results in blocks corresponding to filling of the ns, np, nd, and nf orbitals
As you have seen, the electron configuration for any element can be predicted using the Aufbau principle, which tells you which orbitals of the atom will be occupied. Moreover, the valence electron configurations of atoms in the same group of the periodic table are similar to each other. Because the electron configuration has such an important influence on the properties of an element, this repeated pattern in the valence electron structure is also manifested as a repeated pattern in chemical properties, giving rise to the relationships we see in the periodic table.
The electron configurations of the elements are presented in Figure \(\PageIndex{1}\), which lists the orbitals in the order in which they are filled. In several cases, the ground state electron configurations are different from those predicted by the Aufbau principle. Some of these anomalies occur as the 3d orbitals are filled. For example, the observed ground state electron configuration of chromium is [Ar]4s13d5 rather than the predicted [Ar]4s23d4. Similarly, the observed electron configuration of copper is [Ar]4s13d10 instead of [Ar]s23d9. The actual electron configuration may be rationalized in terms of an added stability associated with a half-filled (ns1, np3, nd5, nf7) or filled (ns2, np6, nd10, nf14) subshell. (In fact, this "special stability" is really another consequence of the instability caused by pairing an electron with another in the same orbital, as illustrated by Hund's rule.) Given the small differences between higher energy levels, this added stability is enough to shift an electron from one orbital to another. In heavier elements, other more complex effects can also be important, leading to many additional anomalies. For example, cerium has an electron configuration of [Xe]6s24f15d1, which is impossible to rationalize in simple terms. In most cases, however, these apparent anomalies do not have important chemical consequences.
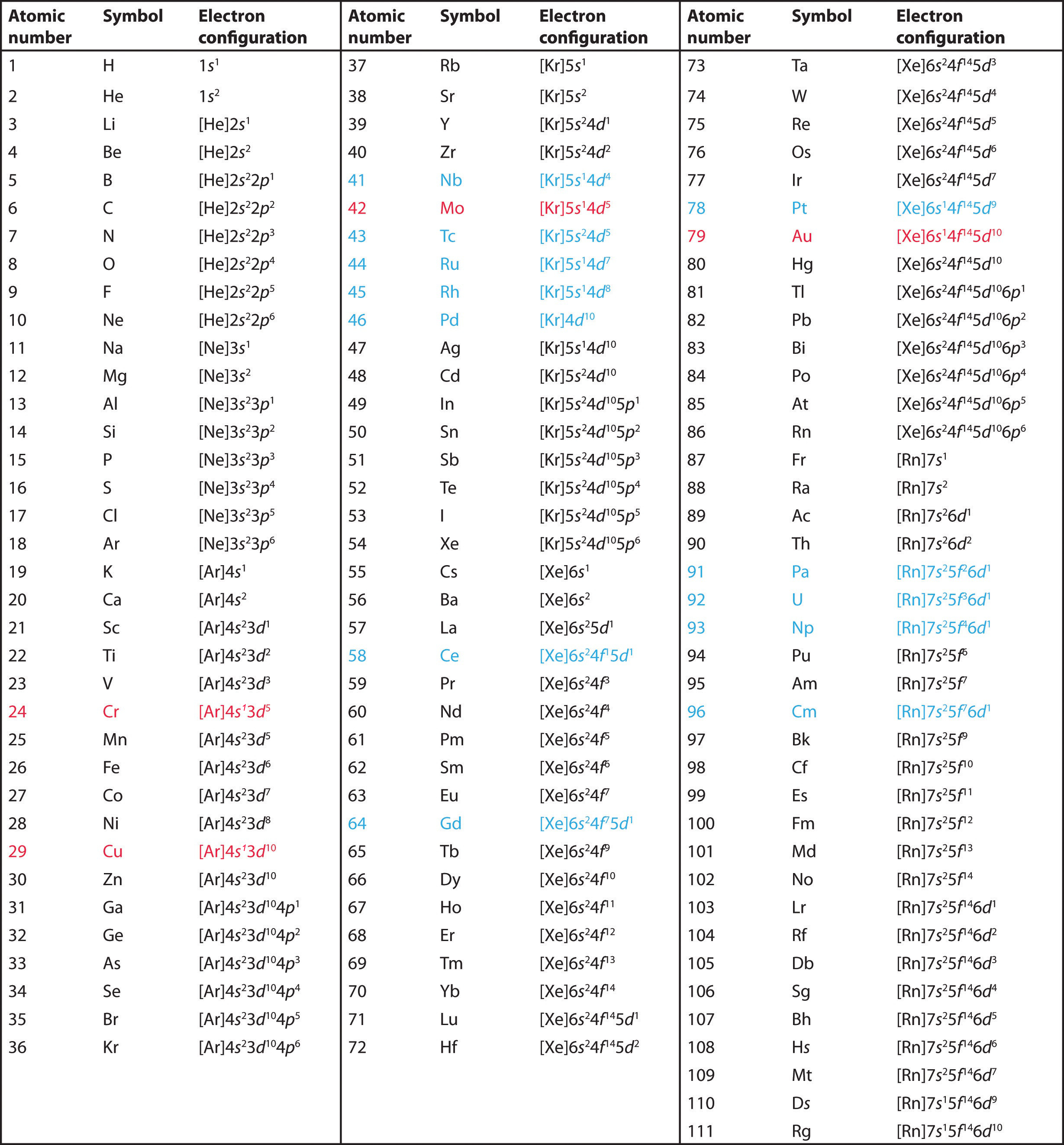
Figure \(\PageIndex{1}\): Electron Configurations of the Elements. The electron configurations of elements indicated in red are exceptions due to the added stability associated with half-filled and filled subshells. The electron configurations of the elements indicated in blue are also anomalous, but the reasons for the observed configurations are more complex. For elements after No, the electron configurations are tentative.
The electron configurations of the elements explain the otherwise peculiar shape of the periodic table. Although the table was originally organized on the basis of physical and chemical similarities between the elements within groups, these similarities are ultimately attributable to orbital energy levels and the Pauli principle, which cause the individual subshells to be filled in a particular order. As a result, the periodic table can be divided into “blocks” corresponding to the type of subshell that is being filled, as illustrated in Figure \(\PageIndex{2}\). For example, the two columns on the left, known as the s block, consist of elements in which the ns orbitals are being filled. The six columns on the right, elements in which the np orbitals are being filled, constitute the p block. In between are the 10 columns of the d block, elements in which the (n − 1)d orbitals are filled. At the bottom lie the 14 columns of the f block, elements in which the (n − 2)f orbitals are filled. Because two electrons can be accommodated per orbital, the number of columns in each block is the same as the maximum electron capacity of the subshell: 2 for ns, 6 for np, 10 for (n − 1)d, and 14 for (n − 2)f. Within each column, each element has the same valence electron configuration—for example, ns1 (group 1) or ns2np1 (group 13). As you will see, this is reflected in important similarities in the chemical reactivity and the bonding for the elements in each column.
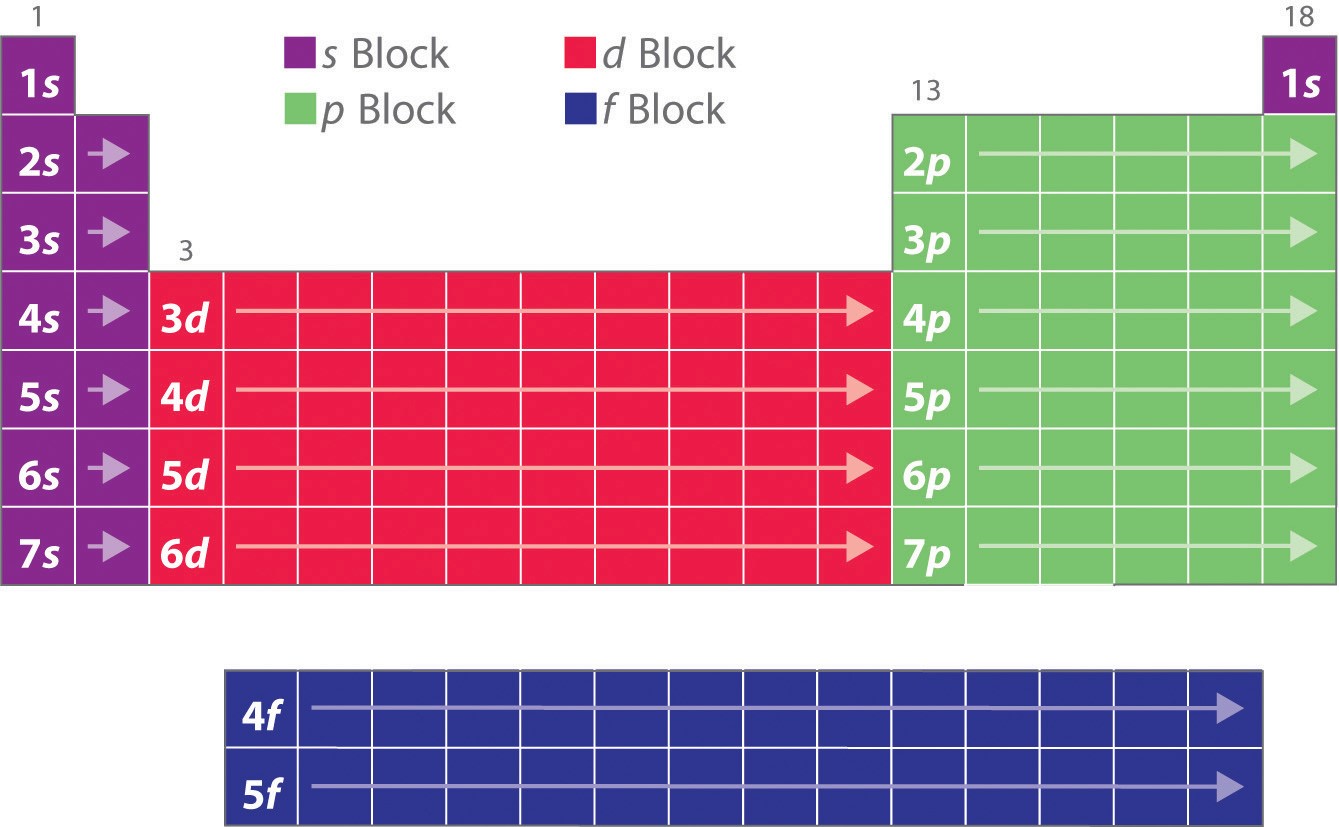
Figure \(\PageIndex{2}\): The Periodic Table, Showing How the Elements Are Grouped According to the Kind of Subshell (s, p, d, f) Being Filled with Electrons in the Valence Shell of Each Element. The electron configurations of the elements are in Figure 6.9.2.
Because each orbital can have a maximum of 2 electrons, there are 2 columns in the s block, 6 columns in the p block, 10 columns in the d block, and 14 columns in the f block.
Hydrogen and helium are placed somewhat arbitrarily. Although hydrogen is not an alkali metal, its 1s1 electron configuration suggests a similarity to lithium ([He]2s1) and the other elements in the first column. Although helium, with a filled ns subshell, should be similar chemically to other elements with an ns2 electron configuration, the closed principal shell dominates its chemistry, justifying its placement above neon on the right.
Example \(\PageIndex{1}\)
Use the periodic table to predict the valence electron configuration of all the elements of group 2 (beryllium, magnesium, calcium, strontium, barium, and radium).
Given: series of elements
Asked for: valence electron configurations
Strategy:
- Identify the block in the periodic table to which the group 2 elements belong. Locate the nearest noble gas preceding each element and identify the principal quantum number of the valence shell of each element.
- Write the valence electron configuration of each element by first indicating the filled inner shells using the symbol for the nearest preceding noble gas and then listing the principal quantum number of its valence shell, its valence orbitals, and the number of valence electrons in each orbital as superscripts.
Solution:
A The group 2 elements are in the s block of the periodic table, and as group 2 elements, they all have two valence electrons. Beginning with beryllium, we see that its nearest preceding noble gas is helium and that the principal quantum number of its valence shell is n = 2.
B Thus beryllium has an [He]s2 electron configuration. The next element down, magnesium, is expected to have exactly the same arrangement of electrons in the n = 3 principal shell: [Ne]s2. By extrapolation, we expect all the group 2 elements to have an ns2 electron configuration.
Exercise \(\PageIndex{1}\)
Use the periodic table to predict the characteristic valence electron configuration of the halogens in group 17.
- Answer
-
All have an ns2np5 electron configuration, one electron short of a noble gas electron configuration. (Note that the heavier halogens also have filled (n − 1)d10 subshells, as well as an (n − 2)f14 subshell for Rn; these do not, however, affect their chemistry in any significant way.
Summary
The arrangement of atoms in the periodic table results in blocks corresponding to filling of the ns, np, nd, and nf orbitals to produce the distinctive chemical properties of the elements in the s block, p block, d block, and f block, respectively.

