3.7: Conformations of Other Alkanes
- Page ID
- 67073
After completing this section, you should be able to
- depict the staggered and eclipsed conformers of propane (or a similar compound) using sawhorse representations and Newman projections.
- sketch a graph of energy versus bond rotation for propane (or a similar compound) and discuss the graph in terms of torsional strain.
- depict the anti, gauche, eclipsed and fully eclipsed conformers of butane (or a similar compound), using sawhorse representations and Newman projections.
- sketch a graph of energy versus ($\ce{\sf{C{2}-C{3}}}$) bond rotation for butane (or a similar compound), and discuss it in terms of torsional and steric repulsion.
- assess which of two (or more) conformers of a given compound is likely to predominate at room temperature from a semi-quantitative knowledge of the energy costs of the interactions involved.
Make certain that you can define, and use in context, the key terms below.
- anti conformation
- gauche conformation
- eclipsed conformation
- steric repulsion
In butane, there are now three rotating carbon-carbon bonds to consider, but we will focus on the middle bond between C2 and C3. Below are two representations of butane in a conformation which puts the two CH3 groups (C1 and C4) in the eclipsed position.

This is the highest energy conformation for butane, due to what is called ‘van der Waals repulsion’, or ‘steric repulsion’, between the two rather bulky methyl groups.
What is van der Waals repulsion? Didn’t we just learn in Chapter 2 that the van der Waals force between two nonpolar groups is an attractive force? Consider this: you probably like to be near your friends, but no matter how close you are you probably don’t want to share a one-room apartment with five of them. When the two methyl groups are brought too close together, the overall resulting noncovalent interaction is repulsive rather than attractive. The result is that their respective electron densities repel one another.
If we rotate the front, (blue) carbon by 60°clockwise, the butane molecule is now in a staggered conformation.

This is more specifically referred to as the ‘gauche’ conformation of butane. Notice that although they are staggered, the two methyl groups are not as far apart as they could possibly be. There is still significant steric repulsion between the two bulky groups. A further rotation of 60°gives us a second eclipsed conformation (B) in which both methyl groups are lined up with hydrogen atoms.

Due to steric repulsion between methyl and hydrogen substituents, this eclipsed conformation B is higher in energy than the gauche conformation. However, because there is no methyl-to-methyl eclipsing, it is lower in energy than eclipsed conformation A.
One more 60 rotation produces the ‘anti’ conformation, where the two methyl groups are positioned opposite each other and steric repulsion is minimized.
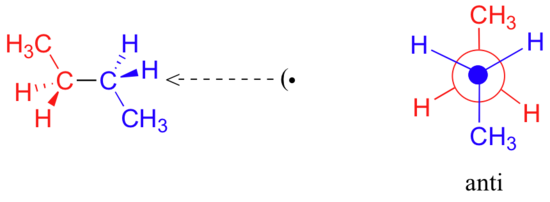
This is the lowest energy conformation for butane.
The diagram below summarizes the relative energies for the various eclipsed, staggered, and gauche conformations.
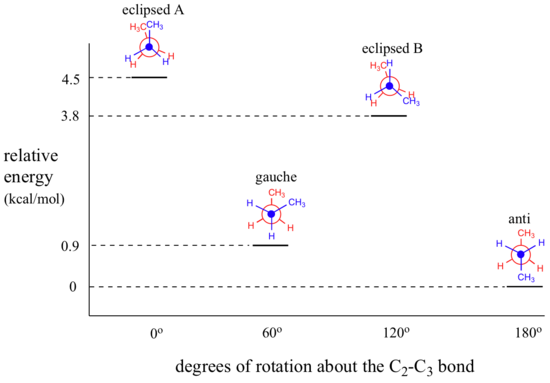

At room temperature, butane is most likely to be in the lowest-energy anti conformation at any given moment in time, although the energy barrier between the anti and eclipsed conformations is not high enough to prevent constant rotation except at very low temperatures. For this reason (and also simply for ease of drawing), it is conventional to draw straight-chain alkanes in a zigzag form, which implies anti conformation at all carbon-carbon bonds.
Drawing Newman Projections
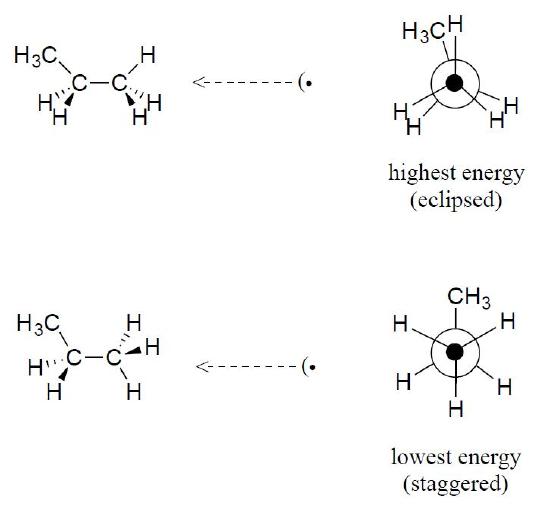
Newman projections are a valuable method for viewing the relative positions of groups within molecule. Being able to draw the Newman projection for a given molecule is a valuable skill and will be used repeatedly throughout organic chemistry. Because organic molecules often contain multiple carbon-carbon bonds it is important to precisely know which bond and which direction is being sighted for the Newman projection. The details of the Newman projection change given the molecule but for typical alkanes a full conformational analysis involves a full 360o rotation in 60o increments. This will produce three staggered conformers and three eclipsed conformers. Typically, the staggered conformers are more stable and the eclipsed conformers are less stable. The least stable conformer will have the largest groups eclipsed while the most stable conformer will have the largest groups anti (180o) to each other.
Example
Draw the Newman projection of 2,3 dimethylbutane along the C2-C3 bond. Then determine the least stable conformation.
First draw the molecule and locate the indicated bond:
Because the question asks for the least stable conformation, focus on the three possible eclipsed Newman projections. Draw out three eclipsed Newman projections as a template. Because it is difficult to draw a true staggered Newman projection, it is common to show the bonds slightly askew.
Place the substituents attached to the second carbon (C3) on the back bonds of all three Newman projections. In this example they are 2 CH3s and an H. Place the substituents in the same position on all three Newman projections.
Then place the substituents attached to the first carbon (C2) on the front bonds of the Newman projection. In this example, the substituents are also 2 CH3s and an H. Move the substituents through two 60o rotations to create the remaining two eclipsed Newman projections. Leave the substituents on the back carbon in place. Attempting to rotate the front and back carbons simultaneously is a common mistake and often leads to incorrect Newman projections.
Compare the Newman projections by looking the eclipsed interactions. Remember that the order of torsional strain interactions are CH3-CH3 > CH3-H > H-H. The third structure has two CH3-CH3 torsional interactions which will make it the least stable conformer of 2,3 dimethyl butane.
Draw Newman projections of the eclipsed and staggered conformations of propane.
- Answer
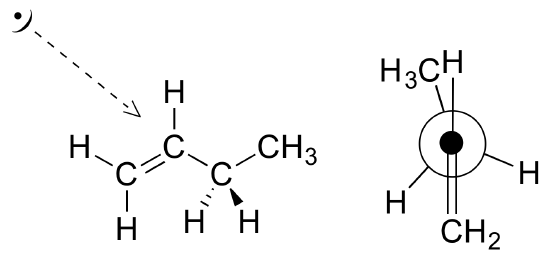
Draw a Newman projection, looking down the C2-C3 bond, of 1-butene in the conformation shown below.
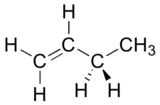
- Answer
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)
Jim Clark (Chemguide.co.uk)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry

