1.2: Atomic Structure- Orbitals
- Page ID
- 67040
After completing this section, you should be able to
- describe the physical significance of an orbital.
- list the atomic orbitals from 1s to 3d in order of increasing energy.
- sketch the shapes of s and p orbitals.
Make certain that you can define, and use in context, the key terms below.
- nodal plane
- node
- orbital
- quantum mechanics
- wave function
Atomic Orbitals
An orbital is the quantum mechanical refinement of Bohr’s orbit. In contrast to his concept of a simple circular orbit with a fixed radius, orbitals are mathematically derived regions of space with different probabilities of having an electron.
One way of representing electron probability distributions was illustrated in Figure 6.5.2 for the 1s orbital of hydrogen. Because Ψ2 gives the probability of finding an electron in a given volume of space (such as a cubic picometer), a plot of Ψ2 versus distance from the nucleus (r) is a plot of the probability density. The 1s orbital is spherically symmetrical, so the probability of finding a 1s electron at any given point depends only on its distance from the nucleus. The probability density is greatest at r = 0 (at the nucleus) and decreases steadily with increasing distance. At very large values of r, the electron probability density is very small but not zero.
In contrast, we can calculate the radial probability (the probability of finding a 1s electron at a distance r from the nucleus) by adding together the probabilities of an electron being at all points on a series of x spherical shells of radius r1, r2, r3,…, rx − 1, rx. In effect, we are dividing the atom into very thin concentric shells, much like the layers of an onion (part (a) in Figure 1.2.1), and calculating the probability of finding an electron on each spherical shell. Recall that the electron probability density is greatest at r = 0 (part (b) in Figure 1.2.1), so the density of dots is greatest for the smallest spherical shells in part (a) in Figure 1.2.1. In contrast, the surface area of each spherical shell is equal to 4πr2, which increases very rapidly with increasing r (part (c) in Figure 1.2.1). Because the surface area of the spherical shells increases more rapidly with increasing r than the electron probability density decreases, the plot of radial probability has a maximum at a particular distance (part (d) in Figure 1.2.1). Most important, when r is very small, the surface area of a spherical shell is so small that the total probability of finding an electron close to the nucleus is very low; at the nucleus, the electron probability vanishes (part (d) in Figure 1.2.1).
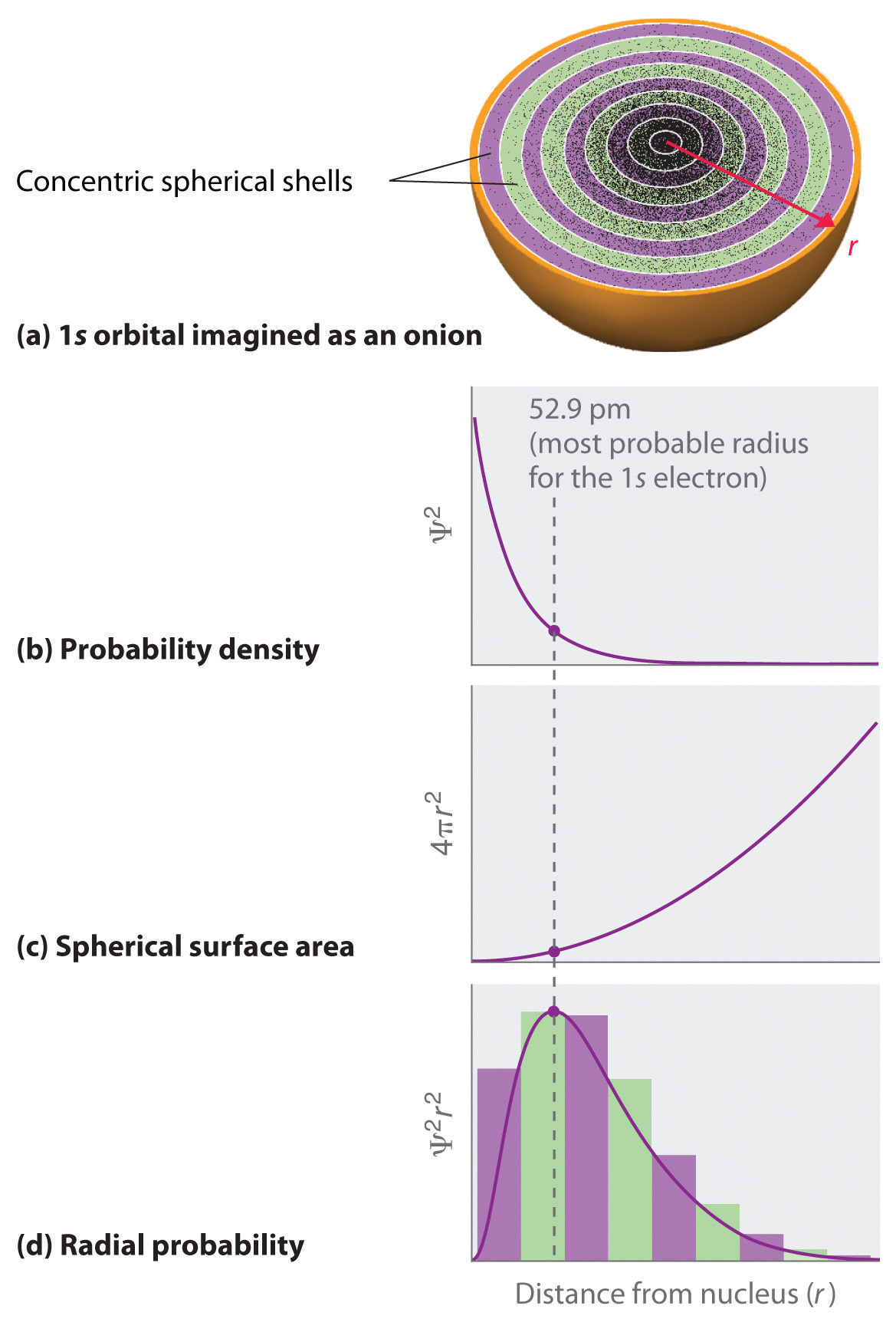
Figure 1.2.1 Most Probable Radius for the Electron in the Ground State of the Hydrogen Atom. (a) Imagine dividing the atom’s total volume into very thin concentric shells as shown in the onion drawing. (b) A plot of electron probability density Ψ2 versus r shows that the electron probability density is greatest at r = 0 and falls off smoothly with increasing r. The density of the dots is therefore greatest in the innermost shells of the onion. (c) The surface area of each shell, given by 4πr2, increases rapidly with increasing r. (d) If we count the number of dots in each spherical shell, we obtain the total probability of finding the electron at a given value of r. Because the surface area of each shell increases more rapidly with increasing r than the electron probability density decreases, a plot of electron probability versus r (the radial probability) shows a peak. This peak corresponds to the most probable radius for the electron, 52.9 pm, which is exactly the radius predicted by Bohr’s model of the hydrogen atom.
For the hydrogen atom, the peak in the radial probability plot occurs at r = 0.529 Å (52.9 pm), which is exactly the radius calculated by Bohr for the n = 1 orbit. Thus the most probable radius obtained from quantum mechanics is identical to the radius calculated by classical mechanics. In Bohr’s model, however, the electron was assumed to be at this distance 100% of the time, whereas in the Schrödinger model, it is at this distance only some of the time. The difference between the two models is attributable to the wavelike behavior of the electron and the Heisenberg uncertainty principle.
Figure 1.2.2 compares the electron probability densities for the hydrogen 1s, 2s, and 3s orbitals. Note that all three are spherically symmetrical. For the 2s and 3s orbitals, however (and for all other s orbitals as well), the electron probability density does not fall off smoothly with increasing r. Instead, a series of minima and maxima are observed in the radial probability plots (part (c) in Figure 1.2.2). The minima correspond to spherical nodes (regions of zero electron probability), which alternate with spherical regions of nonzero electron probability.
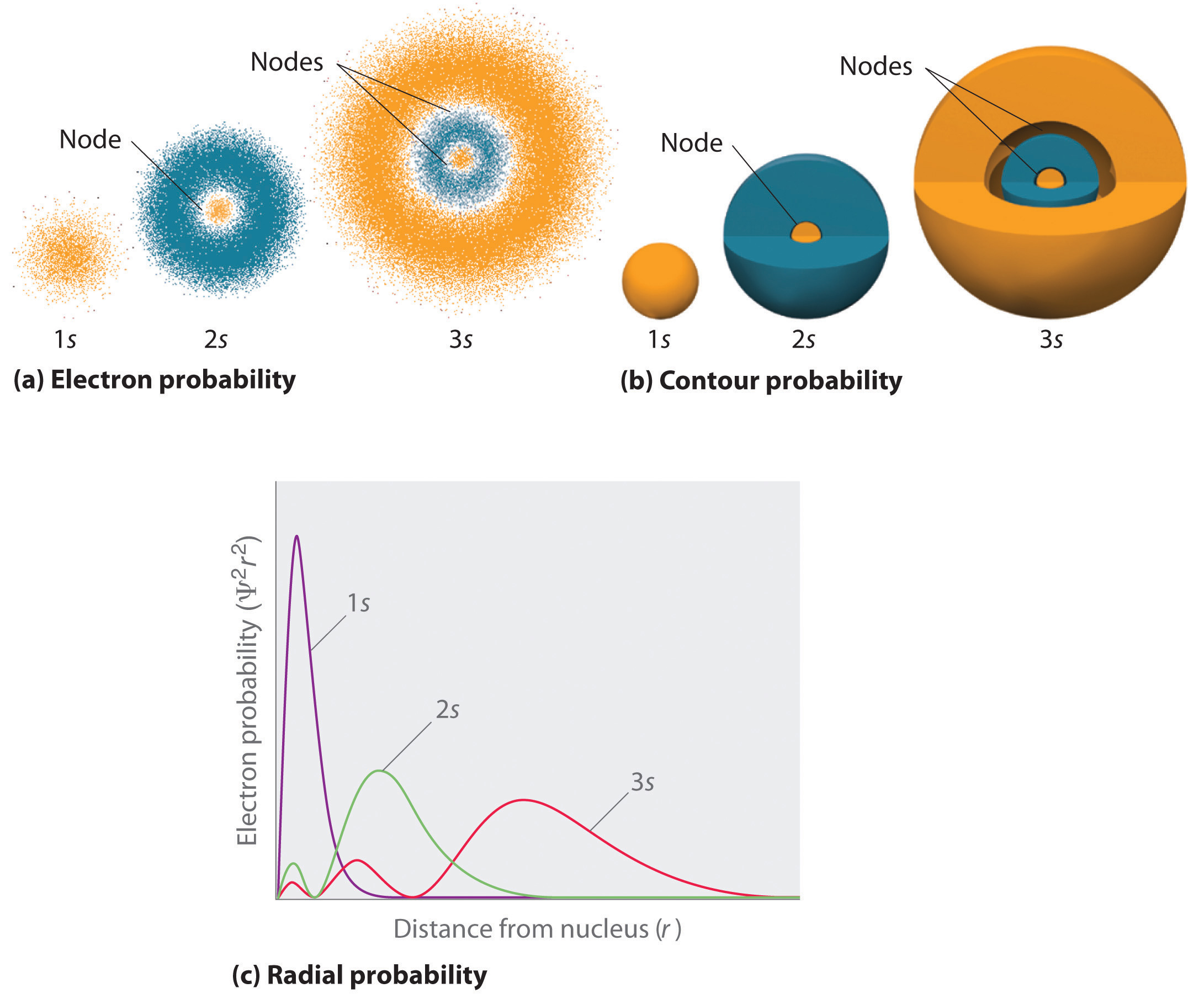
Figure 1.2.2: Probability Densities for the 1s, 2s, and 3s Orbitals of the Hydrogen Atom. (a) The electron probability density in any plane that contains the nucleus is shown. Note the presence of circular regions, or nodes, where the probability density is zero. (b) Contour surfaces enclose 90% of the electron probability, which illustrates the different sizes of the 1s, 2s, and 3s orbitals. The cutaway drawings give partial views of the internal spherical nodes. The orange color corresponds to regions of space where the phase of the wave function is positive, and the blue color corresponds to regions of space where the phase of the wave function is negative. (c) In these plots of electron probability as a function of distance from the nucleus (r) in all directions (radial probability), the most probable radius increases as n increases, but the 2s and 3s orbitals have regions of significant electron probability at small values of r.
s Orbitals
Three things happen to s orbitals as n increases (Figure 1.2.2):![]()
- They become larger, extending farther from the nucleus.
- They contain more nodes. This is similar to a standing wave that has regions of significant amplitude separated by nodes, points with zero amplitude.
- For a given atom, the s orbitals also become higher in energy as n increases because of their increased distance from the nucleus.
Orbitals are generally drawn as three-dimensional surfaces that enclose 90% of the electron density, as was shown for the hydrogen 1s, 2s, and 3s orbitals in part (b) in Figure 1.2.2. Although such drawings show the relative sizes of the orbitals, they do not normally show the spherical nodes in the 2s and 3s orbitals because the spherical nodes lie inside the 90% surface. Fortunately, the positions of the spherical nodes are not important for chemical bonding.
p Orbitals
Only s orbitals are spherically symmetrical. As the value of l increases, the number of orbitals in a given subshell increases, and the shapes of the orbitals become more complex. Because the 2p subshell has l = 1, with three values of ml (−1, 0, and +1), there are three 2p orbitals.

Figure 1.2.3: Electron Probability Distribution for a Hydrogen 2p Orbital. The nodal plane of zero electron density separates the two lobes of the 2p orbital. As in Figure 1.2.2, the colors correspond to regions of space where the phase of the wave function is positive (orange) and negative (blue).
The electron probability distribution for one of the hydrogen 2p orbitals is shown in Figure 1.2.3. Because this orbital has two lobes of electron density arranged along the z axis, with an electron density of zero in the xy plane (i.e., the xy plane is a nodal plane), it is a 2pz orbital. As shown in Figure 1.2.4, the other two 2p orbitals have identical shapes, but they lie along the x axis (2px) and y axis (2py), respectively. Note that each p orbital has just one nodal plane. In each case, the phase of the wave function for each of the 2p orbitals is positive for the lobe that points along the positive axis and negative for the lobe that points along the negative axis. It is important to emphasize that these signs correspond to the phase of the wave that describes the electron motion, not to positive or negative charges.
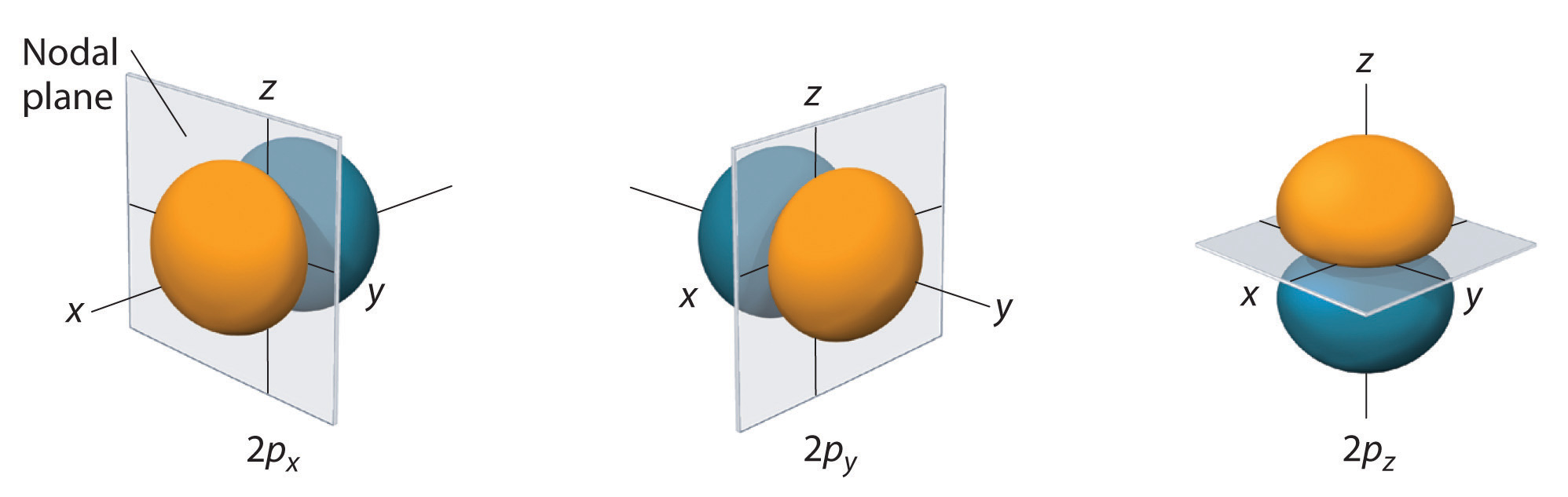
Figure 1.2.4 The Three Equivalent 2p Orbitals of the Hydrogen Atom
The surfaces shown enclose 90% of the total electron probability for the 2px, 2py, and 2pz orbitals. Each orbital is oriented along the axis indicated by the subscript and a nodal plane that is perpendicular to that axis bisects each 2p orbital. The phase of the wave function is positive (orange) in the region of space where x, y, or z is positive and negative (blue) where x, y, or z is negative.
Just as with the s orbitals, the size and complexity of the p orbitals for any atom increase as the principal quantum number n increases. The shapes of the 90% probability surfaces of the 3p, 4p, and higher-energy p orbitals are, however, essentially the same as those shown in Figure 1.2.4.
he electron configuration of an atom is the representation of the arrangement of electrons distributed among the orbital shells and subshells. Commonly, the electron configuration is used to describe the orbitals of an atom in its ground state, but it can also be used to represent an atom that has ionized into a cation or anion by compensating with the loss of or gain of electrons in their subsequent orbitals. Many of the physical and chemical properties of elements can be correlated to their unique electron configurations. The valence electrons, electrons in the outermost shell, are the determining factor for the unique chemistry of the element.
Electron Configurations
Before assigning the electrons of an atom into orbitals, one must become familiar with the basic concepts of electron configurations. Every element on the periodic table consists of atoms, which are composed of protons, neutrons, and electrons. Electrons exhibit a negative charge and are found around the nucleus of the atom in electron orbitals, defined as the volume of space in which the electron can be found within 95% probability. The four different types of orbitals (s,p,d, and f) have different shapes, and one orbital can hold a maximum of two electrons. The p, d, and f orbitals have different sublevels, thus can hold more electrons.
As stated, the electron configuration of each element is unique to its position on the periodic table. The energy level is determined by the period and the number of electrons is given by the atomic number of the element. Orbitals on different energy levels are similar to each other, but they occupy different areas in space. The 1s orbital and 2s orbital both have the characteristics of an s orbital (radial nodes, spherical volume probabilities, can only hold two electrons, etc.) but, as they are found in different energy levels, they occupy different spaces around the nucleus. Each orbital can be represented by specific blocks on the periodic table. The s-block is the region of the alkali metals including helium (Groups 1 & 2), the d-block are the transition metals (Groups 3 to 12), the p-block are the main group elements from Groups 13 to 18, and the f-block are the lanthanides and actinides series.
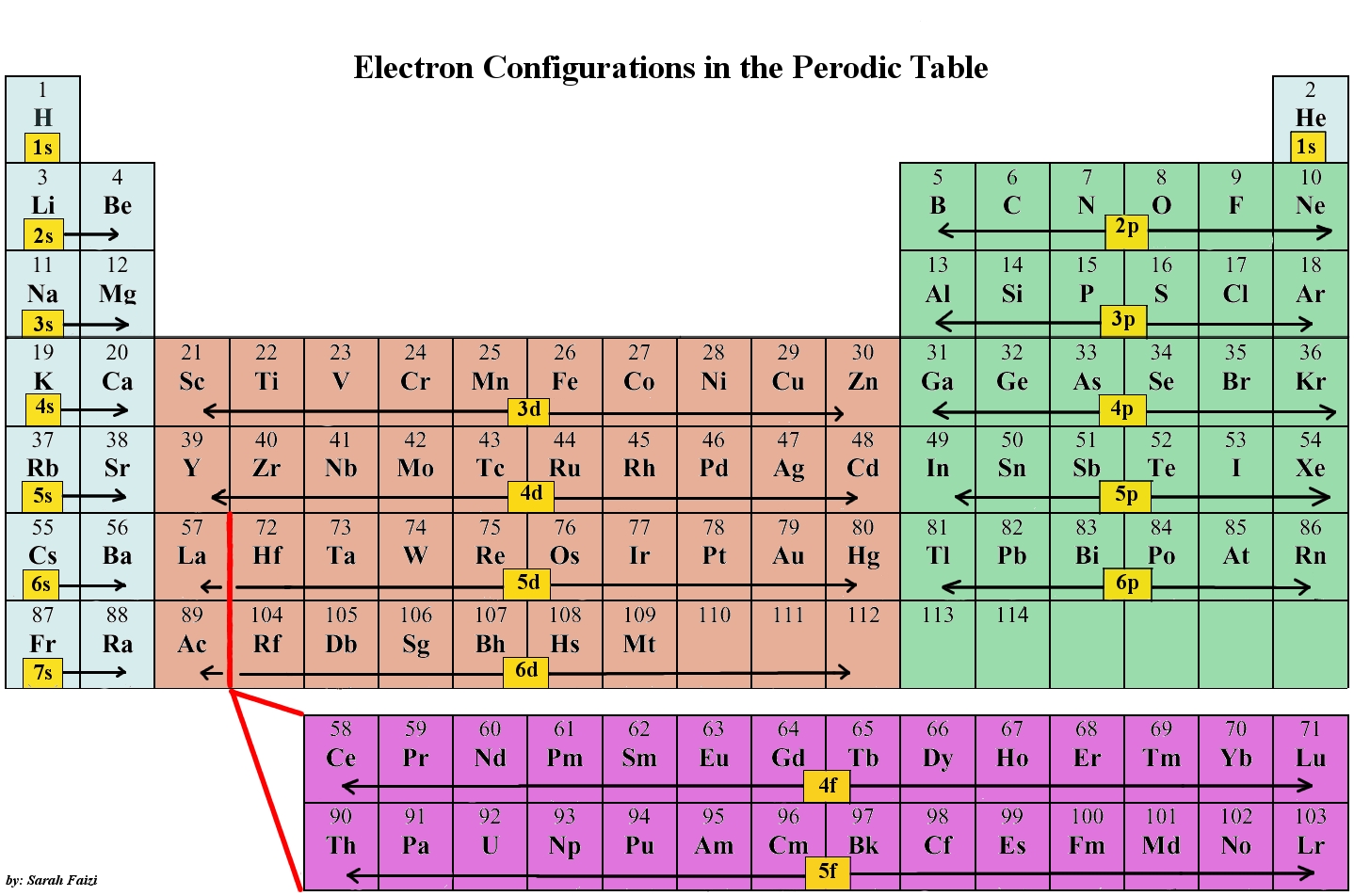
Using the periodic table to determine the electron configurations of atoms is key, but also keep in mind that there are certain rules to follow when assigning electrons to different orbitals. The periodic table is an incredibly helpful tool in writing electron configurations. For more information on how electron configurations and the periodic table are linked, visit the Connecting Electrons to the Periodic Table module.
Rules for Assigning Electron Orbitals
Occupation of Orbitals
Electrons fill orbitals in a way to minimize the energy of the atom. Therefore, the electrons in an atom fill the principal energy levels in order of increasing energy (the electrons are getting farther from the nucleus). The order of levels filled looks like this:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, and 7p
One way to remember this pattern, probably the easiest, is to refer to the periodic table and remember where each orbital block falls to logically deduce this pattern. Another way is to make a table like the one below and use vertical lines to determine which subshells correspond with each other.

The number of valence electrons
The number of valence electrons of an element can be determined by the periodic table group (vertical column) in which the element is categorized. With the exception of groups 3–12 (the transition metals), the units digit of the group number identifies how many valence electrons are associated with a neutral atom of an element listed under that particular column.

The periodic table of the chemical elements
| Periodic table group | Valence electrons |
|---|---|
| Group 1: alkali metals | 1 |
| Group 2: alkaline earth metals | 2 |
| Groups 3-12: transition metals | 2* (The 4s shell is complete and cannot hold any more electrons) |
| Group 13: boron group | 3 |
| Group 14: carbon group | 4 |
| Group 15: pnictogens | 5 |
| Group 16: chalcogens | 6 |
| Group 17: halogens | 7 |
| Group 18: noble gases | 8** |
* The general method for counting valence electrons is generally not useful for transition metals. Instead the modified d electron count method is used.
** Except for helium, which has only two valence electrons.
Exercises
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

