7.4: Balancing Chemical Equations

⚙️ Learning Objectives

• Explain the roles of subscripts and coefficients in chemical equations.
• Balance a chemical equation when given the unbalanced equation.
• Explain the role of the law of conservation of matter in a chemical reaction.

Even though chemical compounds are broken up and new compounds are formed during a chemical reaction, atoms in the reactants do not disappear, nor do new atoms appear to form the products. In chemical reactions, atoms are never created or destroyed. The same atoms that were present in the reactants are present in the products – they are merely reorganized into different arrangements. In a complete chemical equation, the same number of atoms must be present on the reactant and the product sides of the equation.
     

Chemical Equations and the Law of Conservation of Matter

In the previous section, the reaction between hydrogen gas and oxygen gas to produce water in the gaseous phase was shown as a chemical equation:

H₂ (g) + O₂ (g) → H₂O (g) 

At the molecular level, the reaction would look something like this:

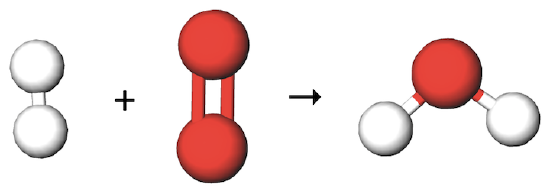
Notice that there are two oxygen atoms on the left hand side of the equation and only one oxygen atom on the right. Where did that one oxygen atom go? Matter can't just disappear. Once again, atoms are never created or destroyed in chemical reactions.

Now, let's consider what happens if we start with two hydrogen molecules and one oxygen molecule:

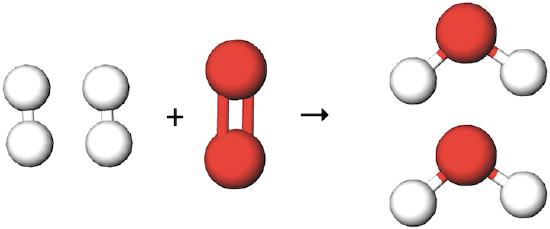
This combination results in two water molecules being formed – there are four hydrogen atoms and two oxygen atoms on the left hand side of the equation and four hydrogen atoms and two oxygen atoms on the right. Any violation of the law of conservation of matter has been avoided. The chemical equation for this reaction above would be written as:

2 H₂ (g) + O₂ (g) → 2 H₂O (g) 

This form of the chemical equation is called a balanced chemical equation. A balanced chemical equation is one that conforms to the law of conservation of matter.
    

Coefficients and Subscripts

There are two types of numbers that appear in chemical equations. There are subscripts, which are part of the chemical formulas of the reactants and products:

\[{\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm H}_{\color[rgb]{0.8, 0.0, 0.0}\boxed2}\;(g)\;+\;{\mathrm O}_{\color[rgb]{0.8, 0.0, 0.0}\boxed2}\;(g)\;\rightarrow{\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm H}_{\color[rgb]{0.8, 0.0, 0.0}\boxed2}\mathrm O\;(g)\nonumber\]

Once the formulas for the reactants and products are determined, the subscripts may not be changed.

There are also coefficients that are placed in front of chemical formulas to indicate how many molecules of that substance are used or produced:

\[{\color[rgb]{0.0, 0.0, 1.0}\boxed2}\;{\mathrm H}_{\color[rgb]{0.8, 0.0, 0.0}2}\;(g)\;+\;{\mathrm O}_{\color[rgb]{0.8, 0.0, 0.0}2}\;(g)\;\rightarrow{\color[rgb]{0.0, 0.0, 1.0}\boxed2}\;{\mathrm H}_{\color[rgb]{0.8, 0.0, 0.0}2}\mathrm O\;(g)\nonumber\]

Coefficients may be changed in order to balance the equation. The equation above indicates that two molecules of hydrogen gas are reacting with one molecule of oxygen gas to produce two molecules of water. 

Because the identities of the reactants and products are fixed, the equation cannot be balanced by changing the subscripts of the reactants or the products. To do so would change the chemical identity of the species being described. For example, had the equation for the reaction:

\[{\mathrm H}_2\;(g)\;+\;{\mathrm O}_2\;(g)\;\rightarrow{\mathrm H}_2\mathrm O\;(g)\nonumber\]

been balanced by changing the subscript for the oxygen on H₂O to become H₂O₂, the reaction no longer shows the production of water. The equation is indeed balanced. However, it shows the production of hydrogen peroxide, a very different substance:

\[\cancel{{\mathrm H}_2\;(g)\;+\;{\mathrm O}_2\;(g)\;\rightarrow\;{\mathrm H}_2{\mathrm O}_{\color[rgb]{0.8, 0.0, 0.0}2}\;(g)}\nonumber\]

Therefore, once again, chemical equations are balanced by changing the coefficients:

\[{\color[rgb]{0.0, 0.0, 1.0}\boxed2}\;{\mathrm H}_2\;(g)\;+\;{\mathrm O}_2\;(g)\;\rightarrow{\color[rgb]{0.0, 0.0, 1.0}\boxed2}\;{\mathrm H}_2\mathrm O\;(g)\nonumber\]

Just like subscripts of "1" are implied in chemical formulas (the formula for water is written as H₂O and not H₂O₁), coefficients of "1" are also implied. In other words, the coefficient for O₂ (g) in the balanced equation above is "1", even though the number "1" is not written.

It may also be helpful to think of coefficients in chemical equations as if they were coefficients in algebra. Coefficients in algebra are written at the front of a term or variable, not in the middle. Just like in algebra, a coefficient in a chemical equation means to multiply. In other words, by writing "2 H₂O", we are indicating a total of 2×2, or 4, hydrogen atoms altogether.
 

Balancing Chemical Equations

The simplest and most generally useful method for balancing chemical equations is called “balancing by inspection,” also known as trial and error. There are some strategies that may be used to reduce the number of trials and errors to wind up with an equation that is ultimately balanced correctly.
 

⚓️ Strategies for Balancing Chemical Equations

1. The most complex formula should usually be balanced first.
2. The simplest formula should usually be balanced last.
3. The least common multiple between two numbers may used to determine the coefficients.
4. Polyatomic ions (if present on both sides of the chemical equation) may be balanced as a unit.
5. Fractional coefficients are sometimes necessary to balance the equation when balancing the simplest formula that remains. If a fractional coefficient has been used, multiply both sides of the equation by the denominator to obtain whole number coefficients.
6. Count the numbers of atoms of each element on each side of the equation to ensure the chemical equation is balanced.

 

✅ Example \(\PageIndex{1}\): Oxidation of Aluminum

Balance the chemical equation for the reaction of aluminum metal with oxygen gas to produce solid aluminum oxide:

Al (s) + O₂ (g) → Al₂O₃ (s)

Solution

1. The most complex formula is Al₂O₃ (s) and should be balanced first, while the simplest formula is Al (s) and should be balanced last.
        
2. There are 2 oxygen atoms on the left and 3 oxygen atoms on the right. The least common multiple between 2 and 3 is 6. To make 6 oxygen atoms on each side, a coefficient of "3" is placed in front of O₂ (g) and a coefficient of "2" is placed in front of Al₂O₃ (s):

Al (s) + 3 O₂ (g) → 2 Al₂O₃ (s)

3. This still leaves aluminum atoms unbalanced. At the point, there is 1 aluminum atom on the left and 4 aluminum atoms on the right. To balance the aluminum atoms, a coefficient of "4" is placed in front of Al (s):

\(\boxed{{\color[rgb]{0.8, 0.0, 0.0}4}\;\mathrm{Al}\;(s)\;+\;{\color[rgb]{0.0, 0.0, 1.0}3}\;{\mathrm O}_2\;(g)\;\rightarrow\;{\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm{Al}}_2{\mathrm O}_3\;(s)}\)

4. A final check should be done to ensure the equation remains balanced for all elements. Sometimes it is useful placing the information into a table and tallying each atom of an element as the equation is being balanced:

\[\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm{Al}&\vert\vert\vert\vert&\vert\vert\vert\vert\\\mathrm O&\cancel{\vert\vert\vert\vert}\;\vert&\cancel{\vert\vert\vert\vert}\;\vert\end{array}\nonumber\]

 

✅ Example \(\PageIndex{2}\): Decomposition of Potassium Chlorate

Balance the chemical equation for the decomposition of solid potassium chlorate in the presence of heat to yield solid potassium chloride and oxygen gas. Note that a triangle appears above the arrow to indicate that heat is necessary for this reaction to occur:

\({\mathrm{KClO}}_3\;(s)\;\xrightarrow\triangle\;\mathrm{KCl}\;(s)\;+\;{\mathrm O}_2\;(g)\)

Solution

1. The most complex formula is KClO₃ (s) and should be balanced first. KCl (s) or O₂ (g) seem to be equally simple. However, it appears that potassium atoms and chlorine atoms are already balanced, so one may begin by balancing the oxygen atoms. Let's keep an ongoing tally this time.

     \(\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactants}&\mathrm{Products}\\\mathrm K&\vert&\vert\\\mathrm{Cl}&\vert&\vert\\\mathrm O&\vert\vert\vert&\vert\vert\end{array}\)

2. There are 3 oxygen atoms on the left and 2 oxygen atoms on the right. The least common multiple between 2 and 3 is 6. To make 6 oxygen atoms on each side, a coefficient of "2" is placed in front of KClO₃ (s) and a coefficient of "3" is placed in front of O₂ (g):

\({\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm{KClO}}_3\;(s)\;\xrightarrow\triangle\;\mathrm{KCl}\;(s)\;+\;{\color[rgb]{0.0, 0.0, 1.0}3}\;{\mathrm O}_2\;(g)\)

\(\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactants}&\mathrm{Products}\\\mathrm K&\vert\vert&\vert\\\mathrm{Cl}&\vert\vert&\vert\\\mathrm O&\cancel{\vert\vert\vert\vert}\;\vert&\cancel{\vert\vert\vert\vert}\;\vert\end{array}\)

3. This now makes both potassium and chlorine atoms unbalanced. However, this is easily remedied by placing a coefficient of "2" is placed in front of KCl (s):

\(\boxed{{\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm{KClO}}_3\;(s)\;\xrightarrow\triangle\;{\color[rgb]{0.8, 0.0, 0.0}2}\;\mathrm{KCl}\;(s)\;+\;{\color[rgb]{0.0, 0.0, 1.0}3}\;{\mathrm O}_2\;(g)}\)

4. A final check should be done to ensure the equation remains balanced for all elements.

\(\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactants}&\mathrm{Products}\\\mathrm K&\vert\vert&\vert\vert\\\mathrm{Cl}&\vert\vert&\vert\vert\\\mathrm O&\cancel{\vert\vert\vert\vert}\;\vert&\cancel{\vert\vert\vert\vert}\;\vert\end{array}\)

 

✅ Example \(\PageIndex{3}\): Combustion of Butane

Balance the chemical equation for the combustion of butane liquid (C₄H₁₀) in the presence of oxygen gas to yield carbon dioxide and water in the gaseous phase:

C₄H₁₀ (l) + O₂ (g) → CO₂ (g) + H₂O (g)

Solution

1. The most complex formula is C₄H₁₀ (l) and should be balanced first, while the simplest formula is O₂ (g) and should be balanced last. Let's keep an ongoing tally once again, this time using numbers.

     \(\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm C&4&1\\\mathrm H&10&2\\\mathrm O&2&3\end{array}\)

2. There are 4 carbon atoms on the left and 1 carbon atom on the right. The least common multiple between 4 and 1 is 4. To make 4 carbon atoms on the right, a coefficient of "4" is placed in front of CO₂ (g):

C₄H₁₀ (l) + O₂ (g) → 4 CO₂ (g) + H₂O (g)

\(\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm C&4&4\\\mathrm H&10&2\\\mathrm O&2&9\end{array}\)

3. There are 10 hydrogen atoms on the left and 2 hydrogen atoms on the right. The least common multiple between 10 and 2 is 10. To make 10 hydrogen atoms on the right, a coefficient of "5" is placed in front of H₂O (g):

C₄H₁₀ (l) + O₂ (g) → 4 CO₂ (g) + 5 H₂O (g)

\(\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm C&4&4\\\mathrm H&10&10\\\mathrm O&2&13\end{array}\)

4. Only oxygen atoms remain unbalanced, as originally desired. At the point, there are 2 oxygen atoms on the left and 13 oxygen atoms on the right. This means it should be possible to place a coefficient (x) in front of  O₂ (g) to balance the equation:

C₄H₁₀ (l) + x O₂ (g) → 4 CO₂ (g) + 5 H₂O (g)

5. It appears  this is the time to employ Strategy #5 listed above, using a fractional coefficient to balance the oxygen atoms, since we need to ask ourselves, "What number times two would equal 13?" In algebra, this question would be written as
   \[2x=13\nonumber\]
   Dividing each side by 2, a solution for x may be found:
   \[x=\frac{13}2\nonumber\]
   In other words, a coefficient of "\(\frac{13}2\)" may placed in front of O₂ (g):

\({\mathrm C}_4{\mathrm H}_{10}\;(l)\;+\;{\textstyle\color[rgb]{0.8, 0.0, 0.0}\frac{13}2}\;{\mathrm O}_2\;(g)\;\rightarrow{\color[rgb]{0.0, 0.0, 1.0}4}\;{\mathrm{CO}}_2\;(g)\;+\;{\color[rgb]{0.6, 0.0, 1.0}5}\;{\mathrm H}_2\mathrm O\;(g)\)

\(\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm C&4&4\\\mathrm H&10&10\\\mathrm O&13&13\end{array}\)

6. As noted in Strategy #5, both sides of the equations should be multiplied by the denominator when fractional coefficients are used in order to obtain whole number coefficients.

\(2\times\left[{\mathrm C}_4{\mathrm H}_{10}\;(l)\;+\;{\textstyle\color[rgb]{0.8, 0.0, 0.0}\frac{13}2}\;{\mathrm O}_2\;(g)\;\rightarrow{\color[rgb]{0.0, 0.0, 1.0}4}\;{\mathrm{CO}}_2\;(g)\;+\;{\color[rgb]{0.6, 0.0, 1.0}5}\;{\mathrm H}_2\mathrm O\;(g)\right]\)

\(\boxed{2\;{\mathrm C}_4{\mathrm H}_{10}\;(l)\;+\;{\color[rgb]{0.8, 0.0, 0.0}13}\;{\mathrm O}_2\;(g)\;\rightarrow{\color[rgb]{0.0, 0.0, 1.0}8}\;{\mathrm{CO}}_2\;(g)\;+\;{\color[rgb]{0.6, 0.0, 1.0}10}\;{\mathrm H}_2\mathrm O\;(g)}\)

7. A final check should be done to ensure the equation remains balanced for all elements.

\(\begin{array}{ccc}\mathrm{Element}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm C&8&8\\\mathrm H&20&20\\\mathrm O&26&26\end{array}\)

 

✏️ Exercise \(\PageIndex{1}\)

Balance the following chemical equations.

1. \(\mathrm V\;(s)\;+\;{\mathrm O}_2\;(g)\;\rightarrow\;{\mathrm V}_2{\mathrm O}_5\;(s)\)
2. \(\mathrm{Mg}\;(s)\;+\;{\mathrm O}_2\;(g)\;\rightarrow\;\mathrm{MgO}\;(s)\)
3. \({\mathrm C}_6{\mathrm H}_{12}{\mathrm O}_6\;(s)\;+\;{\mathrm O}_2\;(g)\;\rightarrow\;{\mathrm{CO}}_2\;(s)\;+\;{\mathrm H}_2\mathrm O\;(l)\)
4. \({\mathrm H}_2{\mathrm O}_2\;(aq)\;\xrightarrow{{\mathrm{MnO}}_2}\;{\mathrm H}_2\mathrm O\;(l)\;+\;{\mathrm O}_2\;(g)\)

Answer A

\({\color[rgb]{0.0, 0.0, 1.0}4}\;\mathrm V\;(s)\;+\;{\color[rgb]{0.0, 0.0, 1.0}5}\;{\mathrm O}_2\;(g)\;\rightarrow\;{\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm V}_2{\mathrm O}_5\;(s)\)

Answer B

\({\color[rgb]{0.0, 0.0, 1.0}2}{\color[rgb]{0.0, 0.0, 1.0}\;}\mathrm{Mg}\;(s)\;+\;{\mathrm O}_2\;(g)\;\rightarrow\;{\color[rgb]{0.0, 0.0, 1.0}2}\;\mathrm{MgO}\;(s)\)

Answer C

\({\mathrm C}_6{\mathrm H}_{12}{\mathrm O}_6\;(s)\;+\;{\color[rgb]{0.0, 0.0, 1.0}6}\;{\mathrm O}_2\;(g)\;\rightarrow\;{\color[rgb]{0.0, 0.0, 1.0}6}\;{\mathrm{CO}}_2\;(s)\;+\;{\color[rgb]{0.0, 0.0, 1.0}6}\;{\mathrm H}_2\mathrm O\;(l)\)

Answer D

\({\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm H}_2{\mathrm O}_2\;(aq)\;\xrightarrow{{\mathrm{MnO}}_2}\;{\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm H}_2\mathrm O\;(l)\;+\;{\mathrm O}_2\;(g)\)

 

✅ Example \(\PageIndex{4}\): Precipitation of Lead(II) Chloride

Aqueous solutions of lead(II) nitrate and sodium chloride are mixed. The products of the reaction are a solid precipitate of lead(II) chloride and an aqueous solution of sodium nitrate. Write the balanced chemical equation for this reaction.

Solution

1. Start by writing out a chemical equation from the word equation. Recall that the nitrate ion (\(\mathrm{NO}_3^-\)) is a polyatomic ion and may be balanced as a unit.

Pb(NO₃)₂ (aq) + NaCl (aq) → PbCl₂ (s) + NaNO₃ (aq)

\(\begin{array}{ccc}\mathrm{Unit}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm{Pb}&\vert&\vert\\{\mathrm{NO}}_3&\vert\vert&\vert\\\mathrm{Na}&\vert&\vert\\\mathrm{Cl}&\vert&\vert\vert\end{array}\)

2. By looking at the tallies, it appears nitrate ions are easily balanced by placing a "2" in front of NaNO₃ (aq). 

Pb(NO₃)₂ (aq) + NaCl (aq) → PbCl₂ (s) + 2 NaNO₃ (aq)

\(\begin{array}{ccc}\mathrm{Unit}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm{Pb}&\vert&\vert\\{\mathrm{NO}}_3&\vert\vert&\vert\vert\\\mathrm{Na}&\vert&\vert\vert\\\mathrm{Cl}&\vert&\vert\vert\end{array}\)

3. At this point, both sodium and chlorine atoms unbalanced. However, this is easily remedied by placing a coefficient of "2" is placed in front of NaCl (aq):

\(\boxed{\mathrm{Pb}{({\mathrm{NO}}_3)}_2\;(aq)\;+\;{\color[rgb]{0.8, 0.0, 0.0}2}\;\mathrm{NaCl}\;(aq)\;\rightarrow\;{\mathrm{PbCl}}_2\;(s)\;+\;{\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm{NaNO}}_3\;(aq)}\)

4. A final check shows the equation is now balanced for all elements.

\(\begin{array}{ccc}\mathrm{Unit}&\mathrm{Reactant}\;\mathrm{Side}&\mathrm{Product}\;\mathrm{Side}\\\mathrm{Pb}&\vert&\vert\\{\mathrm{NO}}_3&\vert\vert&\vert\vert\\\mathrm{Na}&\vert\vert&\vert\vert\\\mathrm{Cl}&\vert\vert&\vert\vert\end{array}\)

 

✏️ Exercise \(\PageIndex{2}\)

Write out a balanced chemical equation for these word equations.

1. Nitrogen gas reacts with hydrogen gas to form gaseous ammonia.
2. Aqueous solutions of aluminum nitrate and lithium carbonate are mixed to yield a solid aluminum carbonate precipitate and an aqueous solution of lithium nitrate.
3. Liquid hexyne (C₆H₁₀) reacts with hydrogen gas in the presence of a platinum catalyst to yield liquid hexane (C₆H₁₄).

Answer A

N₂ (g) + 3 H₂ (g) → 2 NH₃ (g)

Answer B

2 Al(NO₃)₃ (aq) + 3 Li₂CO₃ (aq) → Al₂(CO₃)₃ (s) + 6 LiNO₃ (aq)

Answer C

\({\mathrm C}_6{\mathrm H}_{10}\;(l)\;+\;{\color[rgb]{0.0, 0.0, 1.0}2}\;{\mathrm H}_2\;(g)\;\xrightarrow{\mathrm{Pt}}\;{\mathrm C}_6{\mathrm H}_{14}\;(l)\)

Summary

• To be useful, chemical equations must always be balanced. Balanced chemical equations have the same number and type of each atom on both sides of the equation.
• The coefficients in a balanced equation must be the simplest whole number ratio. Mass is always conserved in chemical reactions.

 

---

This page is shared under a CK-12 license and was authored, remixed, and/or curated by Lance S. Lund (Anoka-Ramsey Community College), Melissa Alviar-Agnew, and Henry Agnew. Original source: https://www.ck12.org/c/chemistry/. 

LICENSED UNDER