1.8: Density and Specific Gravity

Learning Objectives

• Define density and specific gravity.
• Perform calculations involving both density and specific gravity.

After trees are cut, logging companies often move these materials down a river to a sawmill where they can be shaped into building materials or other products. The logs float on the water because they are less dense than the water they are in. Knowledge of density is important in the characterization and separation of materials. Information about density allows us to make predictions about the behavior of matter.

Density

A golf ball and a table tennis ball are about the same size. However, the golf ball is much heavier than the table tennis ball. Now imagine a similar size ball made out of lead. That would be very heavy indeed! What are we comparing? By comparing the mass of an object relative to its size, we are studying a property called density. Density is the ratio of the mass of an object to its volume.

\[ \begin{align} \text{density} &= \dfrac{\text{mass}}{\text{volume}} \label{eq1} \\[4pt] D &= \dfrac{m}{V} \label{eq2} \end{align}\]

Density is usually a measured property of a substance, so its numerical value affects the significant figures in a calculation. Notice that density is defined in terms of two dissimilar units, mass and volume. Common units for density include g/mL, g/cm³, g/L, kg/L, and even kg/m³. Densities for some common substances are listed in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Densities of Some Common Substances

Liquids and Solids	Density at \(20^\text{o} \text{C} \: \left( \text{g/mL} \right)\)	Gases	Density at \(20^\text{o} \text{C} \: \left( \text{g/L} \right)\)
Ethanol	0.79	Hydrogen	0.084
Ice \(\left( 0^\text{o} \text{C} \right)\)	0.917	Helium	0.166
Corn oil	0.922	Air	1.20
Water	0.998	Oxygen	1.33
Water \(\left( 4^\text{o} \text{C} \right)\)	1.000	Carbon dioxide	1.83
Corn syrup	1.36	Radon	9.23
Aluminum	2.70
Copper	8.92
Lead	11.35
Mercury	13.6
Gold	19.3

The SI units of density are kilograms per cubic meter \(\left( \text{kg/m}^3 \right)\), since the \(\text{kg}\) and the \(\text{m}\) are the SI units for mass and length respectively. In everyday usage in a laboratory, this unit is awkwardly large. Most solids and liquids have densities that are conveniently expressed in grams per cubic centimeter \(\left( \text{g/cm}^3 \right)\). Since a cubic centimeter is equal to a milliliter, density units can also be expressed as \(\text{g/mL}\). Water has a density of \(1.0 \: \text{g/mL}\). Gases are much less dense than solids and liquids, so their densities are often reported in \(\text{g/L}\).

Figure \(\PageIndex{1}\): Separatory Funnel containing oil and colored water to display density differences. (CC BY-SA 3.0; PRHaney vai Wikipedia).

If a substance's relative density is less than one then it is less dense than water. If greater than 1, then the substance is denser than water. If the relative density is exactly 1 then the densities are equal. For example, an ice cube, with a relative density of about 0.91 g/mL, will float on water and a substance with a relative density greater than 1 will sink. Corn syrup, being denser, would sink if placed in water.

Since most materials expand as temperature increases, the density of a substance is temperature dependent and usually decreases as temperature increases. For example, cooking oil becomes less dense when heated in a pan.

Density as a Conversion Factor

Conversion factors can also be constructed for converting between different kinds of units. For example, density can be used to convert between the mass and the volume of a substance. Consider mercury, which is a liquid at room temperature and has a density of 13.6 g/mL. The density tells us that 13.6 g of mercury have a volume of 1 mL. We can write that relationship as follows:

13.6 g mercury = 1 mL mercury

This relationship can be used to construct two conversion factors:

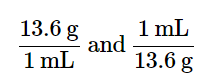
Which one do we use? It depends, as usual, on the units we need to cancel and introduce. For example, suppose we want to know the mass of 16 mL of mercury. We would use the conversion factor that has milliliters on the bottom (so that the milliliter unit cancels) and grams on top so that our final answer has a unit of mass:

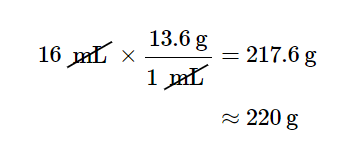
In the last step, we limit our final answer to two significant figures because the volume quantity has only two significant figures; the 1 in the volume unit is considered an exact number, so it does not affect the number of significant figures. The other conversion factor would be useful if we were given a mass and asked to find volume, as the following example illustrates.

Density can be used as a conversion factor between mass and volume.

Example \(\PageIndex{1}\)

An \(18.2 \: \text{g}\) sample of zinc metal has a volume of \(2.55 \: \text{cm}^3\). Calculate the density of zinc.

Solution

Step 1: List the known quantities and plan the problem.

Known

• Mass \(= 18.2 \: \text{g}\)
• Volume \(= 2.55 \: \text{cm}^3\)

Unknown

• Density \(= ? \: \text{g/cm}^3\)

Use Equation \ref{eq1} to solve the problem.

Step 2: Calculate

\[D = \frac{m}{V} = \frac{18.2 \: \text{g}}{2.55 \: \text{cm}^3} = 7.14 \: \text{g/cm}^3\]

Step 3: Think about your result.

\(1 \: \text{cm}^3\) of zinc has a mass of 7.14 grams. Metals are expected to have a density greater than that of water and zinc's density falls within the range of the other metals listed above.

Since density values are known for many substances, density can be used to determine an unknown mass or an unknown volume. Dimensional analysis will be used to ensure that units cancel appropriately.

Example \(\PageIndex{2}\)

What is the mass of \(2.49 \: \text{cm}^3\) of aluminum?

Solution

Step 1: List the known quantities and plan the problem.

Known

• Density \(= 2.70 \: \text{g/cm}^3\)
• Volume \(= 2.49 \: \text{cm}^3\)

Unknown

• Mass \(= ? \: \text{g}\)

Use the equation for density, \(D = \frac{m}{V}\), and dimensional analysis to solve each problem.

Step 2: Calculate

\[ \: \: 2.49 \: \text{cm}^3 \times \frac{2.70 \: \text{g}}{1 \: \text{cm}^3} = 6.72 \: \text{g}\]

In this problem, the mass is equal to the density multiplied by the volume.

Step 3: Think about your results.

Because a mass of \(1 \: \text{cm}^3\) of aluminum is \(2.70 \: \text{g}\), the mass of about \(2.5 \: \text{cm}^3\) should be about 2.5 times larger.

Example \(\PageIndex{3}\)

What is the volume of \(50.0 \: \text{g}\) of aluminum?

Solution

Step 1: List the known quantities and plan the problem.

Known

• Density \(= 2.70 \: \text{g/cm}^3\)
• Mass \(= 50.0 \: \text{g}\)

Unknown

• Volume \(= ? \: \text{cm}^3\)

Use the equation for density, \(D = \frac{m}{V}\), and dimensional analysis to solve each problem.

Step 2: Calculate

\[ \: \: 50.0 \: \text{g} \times \frac{1 \: \text{cm}^3}{2.70 \: \text{g}} = 18.5 \: \text{cm}^3\]

In this problem 2, the volume is equal to the mass divided by the density.

Step 3: Think about your results.

The \(50 \: \text{g}\) of aluminum is substantially more than its density, so that amount should occupy a relatively large volume.

Specific Gravity

Specific gravity is the ratio of the density (mass of a unit volume) of a substance to the density of water,

\[\text{specific gravity} = \dfrac{\text{Density of a substance}(\cancel{g/mL})}{\text{Density of the water at the same temperature}(\cancel{g/mL})}\]

The units cancel out in the ratio. Therefore, the specific gravity is a unitless number. The density of water is 1.0 g/mL at room temperature, so the specific gravity is equal to the density of the object expressed without a unit.

Example \(\PageIndex{1}\)

At 20.0^oC, the density of ethanol is 0.790 g/mL and that of water is 1.00 g/mL. What is the specific gravity of ethanol at 20.0^oC?

Solution

The units cancel out and so specific gravity is a unitless quantity.

Exercise \(\PageIndex{1}\)

At 20.0^oC, the density of mercury is 13.6 g/mL and that of water is 1.00 g/mL. What is the specific gravity of mercury at 20.0^oC?.

Answer

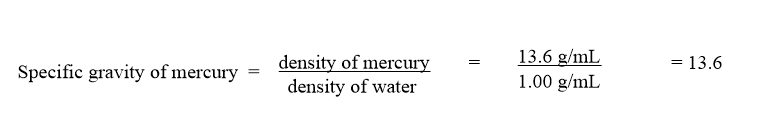
A hydrometer is an instrument used for measuring the specific density of liquids based on the concept of buoyancy (Figure \(\PageIndex{2}\)). A hydrometer usually consists of a sealed hollow glass tube with a wider bottom portion for buoyancy, a ballast such as lead or mercury for stability, and a narrow stem with graduations for measuring. The liquid to test is poured into a tall container, often a graduated cylinder, and the hydrometer is gently lowered into the liquid until it floats freely. The point at which the surface of the liquid touches the stem of the hydrometer correlates to relative density. Hydrometers can contain any number of scales along the stem corresponding to properties correlating to the density.

Figure \(\PageIndex{2}\): A US Navy Aviation Boatswain's Mate tests the specific gravity of JP-5 fuel. (Public Domain; U.S. Navy via Wikipedia)

When substances dissolve in water, the specific gravity of the solution is usually different from pure water. For example, the specific gravity of whole blood for humans is ~1.060. The density of urine varies in the range of 1.005 to 1.030. Both the blood and urine have dissolved substances in water that increase the density from that of pure water. Both high and low density or specific gravity than the normal range of urine indicates medical problems. An increase in the specific gravity of urine indicates that it is due to an increase in the solutes caused by dehydration, diarrhea, or infection. Similarly, a decrease in solute concentration decreases the specific gravity of urine, which indicates medical problems like renal failure.

The density of urine can be affected by a variety of medical conditions. Patients who suffer from diabetes produce an abnormally large volume of urine with a relatively low density. In another form of diabetes, called diabetes mellitus, there is excess glucose dissolved in the urine so the density of urine is abnormally high. The density of urine may also be abnormally high because of excess protein in the urine, which can be caused by congestive heart failure or certain renal (kidney) problems. Thus, a urine specific gravity test can provide clues to various kinds of health problems.

Summary

• Density is the ratio of the mass of an object to its volume.
• Gases are less dense than solids and liquids.
• For liquids and gases, the temperature will affect the density to some extent.
• Specific gravity is the ratio of the density of a substance to the density of water.

Contributors and Attributions

• Deboleena Roy (American River College)

• Elizabeth R. Gordon (Furman University)