Potential Energy
- Page ID
- 1957
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\(\newcommand{\ket}[1]{\left| #1 \right>} \)
\( \newcommand{\bra}[1]{\left< #1 \right|} \)
\( \newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>} \)
\( \newcommand{\qmvec}[1]{\mathbf{\vec{#1}}} \)
\( \newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
\( \newcommand{\expect}[1]{\langle #1 \rangle}\)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Potential Energy is the energy due to position, composition, or arrangement. Also, it is the energy associated with forces of attraction and repulsion between objects. Any object that is lifted from its resting position has stored energy therefore it is called potential energy because it has a potential to do work when released.
Introduction
For example, when a ball is released from a certain height, it is pulled by gravity and the potential energy is converted to kinetic energy during the fall. As this energy converts from potential to kinetic, it is important to take into consideration that energy cannot be created nor destroyed (law of conservation of energy). This potential energy becomes kinetic energy as the ball accelerates towards the ground. The object's total energy can be found through the sum of these to energies.
In an exothermic chemical reaction, potential energy is the source of energy. During an exothermic reaction bonds break and new bonds form and protons and electrons go from a structure of higher potential energy to lower potential energy. During this change, potential energy is converted to kinetic energy, which is the heat released in reactions. In an endothermic reaction the opposite occurs. The protons and electrons move from an area of low potential energy to an area of high. This takes in energy.
Potential Energy on a molecular level: Energy stored in bonds and static interactions are:
- Covalent bonds
- Electrostatic forces
- Nuclear forces
Gravitational Potential Energy
\[PE= Fx\]
where \(F\) is the opposing force and \(x\) is the distance moved. To calculate the potential energy of an object on Earth or within any other force field the formula
\[PE=mgh \label{pe1}\]
with
- \(m\) is the mass of the object in kilograms
- \(g\) is the acceleration due to gravity. On Earth this is 9.8 meters/seconds2
- \(h\) is the object's height. The height should be in meters.
If the units above are used for the \(m\), \(g\), and \(h\), then the final answer should be given in Joules.
A 15 gram ball sits on top of a 2 m high refrigerator. What is the potential energy of the ball at the top of the refrigerator?
Solution
Use Equation \ref{pe1} with \(m =15\, grams\). This mass however has to be in kilograms. The conversion to grams to kilograms is: 1,000 grams per 1 kg
- \(\text{height}=2\, m\)
- \(g=9.8 \, m/s^2\)
\[PE=(0.015 \, kg)(9.8 \, m/s^2)(2\,m)=0.294\, J \nonumber\]
What is the mass of a cart full of groceries that is sitting on top of a 2 m hill if its gravitational potential energy is 0.3 J?
Solution
Use Equation \ref{pe1}
\[0.3\,J=(m)(9.8\, m/s^2)(2\,m) \nonumber\]
and solve for mass
\[m=0.015 \,kg=15\, g. \nonumber\]
A 200 gram weight is placed on top of a shelf with a potential energy of 5 J. How high is the weight resting?
Solution
\[5\,J=\left(\dfrac{200\,g}{1000\,g/kg}\right)(9.8 m/s^2)(h) \nonumber\]
and solve for height
\[h=2.55\, m \nonumber\]
Coulombic Potential Energy
The potential energy of two charged particles at a distance can be found through the equation:
\[E= \dfrac{q_1 q_2}{4π \epsilon_o r} \label{Coulomb}\]
where
- \(r\) is distance
- \(q_1\) and \(q_2\) are the charges
- \(ε_0= 8.85 \times 10^{-12} C^2/J\,m\)
For charges with the same sign, \(E\) has a + sign and tends to get smaller as \(r\) increases. This can explain why like charges repel each other. Systems prefer a low potential energy and thus repel each other which increases the distance between them and lowers the potential energy.
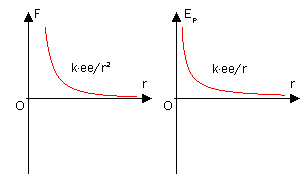
For charges with different charges, the opposite of what is stated above is true. E has a - sign which becomes even more negative as the opposite charged particles attract, or come closer together.
Calculate the potential energy associated with two particles with charges of \(3 \times 10^{-6}\, C\) and \(3.9 \times 10^{-6}\, C\) are separated by a distance of \(1\, m\)
Solution
Using Equation \ref{Coulomb}
\[\begin{align*} E &=\dfrac{(3\times 10^{-6}\,C)(3.9 \times 10^{-6}\,C)}{4π \,8.85 \times 10^{-12} \,C^2/Jm} \\[4pt] &=0.105 \,J \end{align*}\]
Find the distance between two particles that have a potential energy of \(0.2\, J\) and charges of \(2.5 \times 10^{-6}\, C\) and \(3.1 \times 10^{-6}\, C\).
Solution
\[\begin{align*} 0.2 &=\dfrac{(2.5 \times 10^{-6}\,C)(3.1 \times 10^{-6} \,C)}{4\pi (8.85 \times 10^{-12} \,C^2/Jm) r} \\[4pt] &=\dfrac{(8.99 \times 10^9)(7.75 \times 10^{-11})}{r} \\[4pt] &=\dfrac{0.6967}{r} \end{align*}\]
cross multiply and solve for \(r\)
\[r=3.5\, m \nonumber\]
Includes all interactions in the system such as: in nucleus of atoms; in atoms; between atoms in a molecule (intra-molecular forces); and between different molecules (inter-molecular forces).
Contributors and Attributions
- Brittanie Harbick (UCD), Laura Suh (UCD), Amrit Paul Bains (UCD)

