Explaining Chemical Equilibria
- Page ID
- 3835
This page looks at the basic ideas underpinning the idea of a chemical equilibrium. It talks about reversible reactions and how they behave if the system is closed. This leads to the idea of a dynamic equilibrium, and what the common term "position of equilibrium" means.
Reversible reactions
A reversible reaction is one which can be made to go in either direction depending on the conditions. If you pass steam over hot iron the steam reacts with the iron to produce a black, magnetic oxide of iron called triiron tetroxide, \(Fe_3O_4\)
\[ 3 Fe (s) + 4H_2 O(g) \rightarrow Fe_3O_4(s) + 4H_2 (g)\]
The hydrogen produced in the reaction is swept away by the stream of steam.
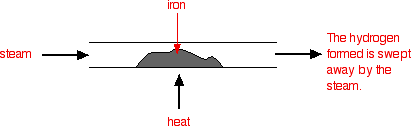
Under different conditions, the products of this reaction will also react together. Hydrogen passed over hot triiron tetroxide reduces it to iron. Steam is also produced.
\[ Fe_3O_4 (s) + 4H_2 (g) \rightarrow 3Fe(s) + 4H_2O (g)\]
This time the steam produced in the reaction is swept away by the stream of hydrogen.

These reactions are reversible, but under the conditions normally used, they become one-way reactions. The products aren't left in contact with each other, so the reverse reaction can't happen.
Reversible reactions happening in a closed system
A Closed System is one in which no substances are either added to the system or lost from it. Energy can, however, be transferred in or out at will. In the example we've been looking at, you would have to imagine iron being heated in steam in a closed container. Heat is being added to the system, but none of the substances in the reaction can escape. The system is closed.
As the triiron tetroxide and hydrogen start to be formed, they will also react again to give the original iron and steam. So, if you analyzed the mixture after a while, what would you find? You would find that you had established what is known as a dynamic equilibrium. To explain what that means, we are going to use a much simpler example . . .
Dynamic equilibria
Imagine a substance which can exist in two forms - a blue form or an orange form - and that each form can react to give the other one. We are going to let them react in a closed system; neither form can escape. Assume that the blue form turns into the orange one much faster than the other way round. In any given time, these are the chances of the two changes happening:
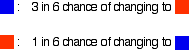
You can simulate this very easily with some coloured paper cut up into small pieces (a different colour on each side), and a dice. The following are the real results of a "reaction". Started with 16 blue squares and looked at each one in turn and decided whether it should change colour by throwing a dice.
- A blue square was turned into an orange square (the bit of paper was turned over!) if I threw a 4, 5 or 6
- An orange square was turned into a blue square only if I threw a 6 while I was looking at that particular square.
Once I had looked at all 16 squares, I started the process all over again - but obviously with a different starting pattern. The diagrams show the results of doing this 11 times (plus the original 16 blue squares).
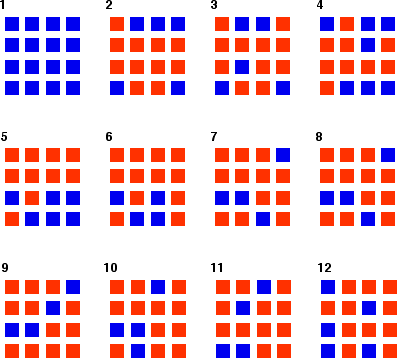
You can see that the "reaction" is continuing all the time. The exact pattern of orange and blue is constantly changing. However, the overall numbers of orange and of blue squares remain remarkably constant - most commonly, 12 orange ones to 4 blue ones.
Explaining the term "dynamic equilibrium"
The reaction has reached equilibrium in the sense that there is no further change in the numbers of blue and orange squares. However, the reaction is still continuing. For every orange square that turns blue, somewhere in the mixture it is replaced by a blue square turning orange. This is known as a dynamic equilibrium. The word dynamic shows that the reaction is still continuing. You can show dynamic equilibrium in an equation for a reaction by the use of special arrows. In the present case, you would write it as:
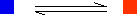
It is important to realize that this doesn't just mean that the reaction is reversible. It means that you have a reversible reaction in a state of dynamic equilibrium.
The change from left to right in the equation (in this case from blue to orange as it is written) is known as the forward reaction. The change from right to left is the back reaction.
In the example above, the equilibrium mixture contained more orange squares than blue ones. Position of equilibrium is a way of expressing this. You can say things like:
- "The position of equilibrium lies towards the orange."
- "The position of equilibrium lies towards the right-hand side."
If the conditions of the experiment change (by altering the relative chances of the forward and back reactions happening), the composition of the equilibrium mixture will also change.
For example, if changing the conditions produced more blue in the equilibrium mixture, you would say "The position of equilibrium has moved to the left" or "The position of equilibrium has moved towards the blue".
Reaching equilibrium from the other side
What happens if you started the reaction with orange squares rather than blue ones, but kept the chances of each change happening the same as in the first example? This is the result of my "reaction".

Once again, you can see that exactly the same position of equilibrium is being established as when we started with the blue squares. You get exactly the same equilibrium mixture irrespective of which side of the equation you start from - provided the conditions are the same in both cases.
A more formal look at dynamic equilibria
This is the equation for a general reaction which has reached dynamic equilibrium:
\[ A + B \rightleftharpoons C + D\]
How did it get to that state? Let's assume that we started with \(A\) and \(B\). At the beginning of the reaction, the concentrations of A and \(B\) were at their maximum. That means that the rate of the reaction was at its fastest. As \(A\) and \(B\) react, their concentrations fall. That means that they are less likely to collide and react, and so the rate of the forward reaction falls as time goes on.
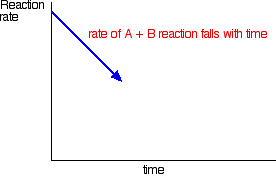
In the beginning, there is not any \(C\) and \(D\), so there can't be any reaction between them. As time goes on, though, their concentrations in the mixture increase and they are more likely to collide and react. With time, the rate of the reaction between \(C\) and \(D\) increases:
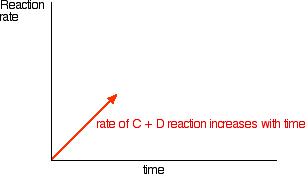
Eventually, the rates of the two reactions will become equal. \(A\) and \(B\) will be converting into \(C\) and \(D\) at exactly the same rate as \(C\) and \(D\) convert back into \(A\) and \(B\) again.
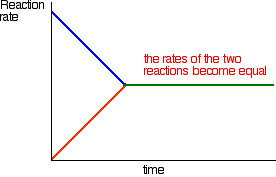
At this point there will not be any further change in the amounts of \(A\), \(B\), \(C\) and \(D\) in the mixture. As fast as something is being removed, it is being replaced again by the reverse reaction. We have reached a position of dynamic equilibrium.
Summary
A dynamic equilibrium occurs when you have a reversible reaction in a closed system. Nothing can be added to the system or taken away from it apart from energy. At equilibrium, the quantities of everything present in the mixture remain constant, although the reactions are still continuing. This is because the rates of the forward and the back reactions are equal. If you change the conditions in a way which changes the relative rates of the forward and back reactions you will change the position of equilibrium - in other words, change the proportions of the various substances present in the equilibrium mixture. This is explored in detail on other pages in this equilibrium section.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


