Lattice Enthalpies and Born Haber Cycles

Lattice enthalpy is a measure of the strength of the forces between the ions in an ionic solid. The greater the lattice enthalpy, the stronger the forces. This page introduces lattice enthalpies (lattice energies) and Born-Haber cycles.

Defining Lattice Enthalpy

There are two different ways of defining lattice enthalpy which directly contradict each other, and you will find both in common use. In fact, there is a simple way of sorting this out, but many sources do not use it. Lattice enthalpy is a measure of the strength of the forces between the ions in an ionic solid. The greater the lattice enthalpy, the stronger the forces. Those forces are only completely broken when the ions are present as gaseous ions, scattered so far apart that there is negligible attraction between them. You can show this on a simple enthalpy diagram.

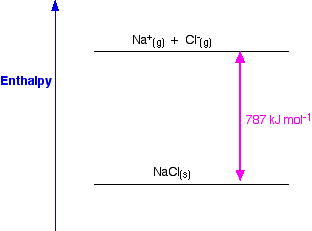
For sodium chloride, the solid is more stable than the gaseous ions by 787 kJ mol^-1, and that is a measure of the strength of the attractions between the ions in the solid. Remember that energy (in this case heat energy) is released when bonds are made, and is required to break bonds.

So lattice enthalpy could be described in either of two ways.

• It could be described as the enthalpy change when 1 mole of sodium chloride (or whatever) was formed from its scattered gaseous ions. In other words, you are looking at a downward arrow on the diagram.
• Or, it could be described as the enthalpy change when 1 mole of sodium chloride (or whatever) is broken up to form its scattered gaseous ions. In other words, you are looking at an upward arrow on the diagram.

Both refer to the same enthalpy diagram, but one looks at it from the point of view of making the lattice, and the other from the point of view of breaking it up. Unfortunately, both of these are often described as "lattice enthalpy".

Definitions

• The lattice dissociation enthalpy is the enthalpy change needed to convert 1 mole of solid crystal into its scattered gaseous ions. Lattice dissociation enthalpies are always positive.
• The lattice formation enthalpy is the enthalpy change when 1 mole of solid crystal is formed from its separated gaseous ions. Lattice formation enthalpies are always negative.

This is an absurdly confusing situation which is easily resolved by never using the term "lattice enthalpy" without qualifying it.

• You should talk about "lattice dissociation enthalpy" if you want to talk about the amount of energy needed to split up a lattice into its scattered gaseous ions. For NaCl, the lattice dissociation enthalpy is +787 kJ mol^-1.
• You should talk about "lattice formation enthalpy" if you want to talk about the amount of energy released when a lattice is formed from its scattered gaseous ions. For NaCl, the lattice formation enthalpy is -787 kJ mol^-1.

That immediately removes any possibility of confusion.

Factors affecting Lattice Enthalpy

The two main factors affecting lattice enthalpy are

• The charges on the ions and
• The ionic radii (which affects the distance between the ions).

The charges on the ions

Sodium chloride and magnesium oxide have exactly the same arrangements of ions in the crystal lattice, but the lattice enthalpies are very different.

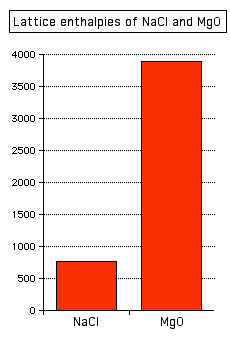
You can see that the lattice enthalpy of magnesium oxide is much greater than that of sodium chloride. That's because in magnesium oxide, 2+ ions are attracting 2- ions; in sodium chloride, the attraction is only between 1+ and 1- ions.

The Radius of the Ions

The lattice enthalpy of magnesium oxide is also increased relative to sodium chloride because magnesium ions are smaller than sodium ions, and oxide ions are smaller than chloride ions. That means that the ions are closer together in the lattice, and that increases the strength of the attractions.

This effect of ion size on lattice enthalpy is clearly observed as you go down a Group in the Periodic Table. For example, as you go down Group 7 of the Periodic Table from fluorine to iodine, you would expect the lattice enthalpies of their sodium salts to fall as the negative ions get bigger - and that is the case:

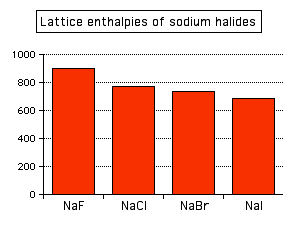
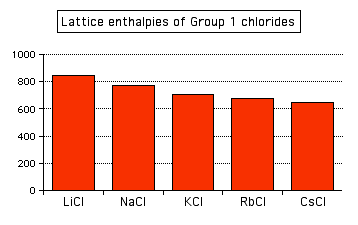
Attractions are governed by the distances between the centers of the oppositely charged ions, and that distance is obviously greater as the negative ion gets bigger. And you can see exactly the same effect if as you go down Group 1. The next bar chart shows the lattice enthalpies of the Group 1 chlorides.

Calculating Lattice Enthalpy

It is impossible to measure the enthalpy change starting from a solid crystal and converting it into its scattered gaseous ions. It is even more difficult to imagine how you could do the reverse - start with scattered gaseous ions and measure the enthalpy change when these convert to a solid crystal. Instead, lattice enthalpies always have to be calculated, and there are two entirely different ways in which this can be done.

1. You can can use a Hess's Law cycle (in this case called a Born-Haber cycle) involving enthalpy changes which can be measured. Lattice enthalpies calculated in this way are described as experimental values.
2. Or you can do physics-style calculations working out how much energy would be released, for example, when ions considered as point charges come together to make a lattice. These are described as theoretical values. In fact, in this case, what you are actually calculating are properly described as lattice energies.

Born-Haber Cycles

Standard Atomization Enthalpies

Before we start talking about Born-Haber cycles, we need to define the atomization enthalpy, \(\Delta H^o_a\). The standard atomization enthalpy is the enthalpy change when 1 mole of gaseous atoms is formed from the element in its standard state. Enthalpy change of atomization is always positive. You are always going to have to supply energy to break an element into its separate gaseous atoms. All of the following equations represent changes involving atomization enthalpy:

\[ \dfrac{1}{2} Cl_2 (g) \rightarrow Cl(g) \;\;\;\; \Delta H^o_a=+122\, kJ\,mol^{-1} \nonumber \]

\[ \dfrac{1}{2} Br_2 (l) \rightarrow Br(g) \;\;\;\; \Delta H^o_a=+122\, kJ\,mol^{-1} \nonumber \]

\[ Na (s) \rightarrow Na(g) \;\;\;\; \Delta H^o_a=+107\, kJ\,mol^{-1} \nonumber \]

Notice particularly that the "mol^-1" is per mole of atoms formed - NOT per mole of element that you start with. You will quite commonly have to write fractions into the left-hand side of the equation. Getting this wrong is a common mistake.

Example \(\PageIndex{1}\): Born-Haber Cycle for \(\ce{NaCl}\)

Consider a Born-Haber cycle for sodium chloride, and then talk it through carefully afterwards. You will see that I have arbitrarily decided to draw this for lattice formation enthalpy. If you wanted to draw it for lattice dissociation enthalpy, the red arrow would be reversed - pointing upwards.

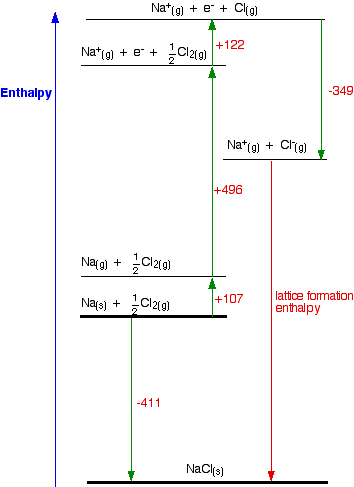
Focus to start with on the higher of the two thicker horizontal lines. We are starting here with the elements sodium and chlorine in their standard states. Notice that we only need half a mole of chlorine gas in order to end up with 1 mole of NaCl. The arrow pointing down from this to the lower thick line represents the enthalpy change of formation of sodium chloride.

The Born-Haber cycle now imagines this formation of sodium chloride as happening in a whole set of small changes, most of which we know the enthalpy changes for - except, of course, for the lattice enthalpy that we want to calculate.

• The +107 is the atomization enthalpy of sodium. We have to produce gaseous atoms so that we can use the next stage in the cycle.
• The +496 is the first ionization energy of sodium. Remember that first ionization energies go from gaseous atoms to gaseous singly charged positive ions.
• The +122 is the atomization enthalpy of chlorine. Again, we have to produce gaseous atoms so that we can use the next stage in the cycle.
• The -349 is the first electron affinity of chlorine. Remember that first electron affinities go from gaseous atoms to gaseous singly charged negative ions.
• And finally, we have the positive and negative gaseous ions that we can convert into the solid sodium chloride using the lattice formation enthalpy.

Now we can use Hess' Law and find two different routes around the diagram which we can equate. As drawn, the two routes are obvious. The diagram is set up to provide two different routes between the thick lines. So, from the cycle we get the calculations directly underneath it . . .

-411 = +107 + 496 + 122 - 349 + LE

LE = -411 - 107 - 496 - 122 + 349

LE = -787 kJ mol^-1

How would this be different if you had drawn a lattice dissociation enthalpy in your diagram? Your diagram would now look like this:

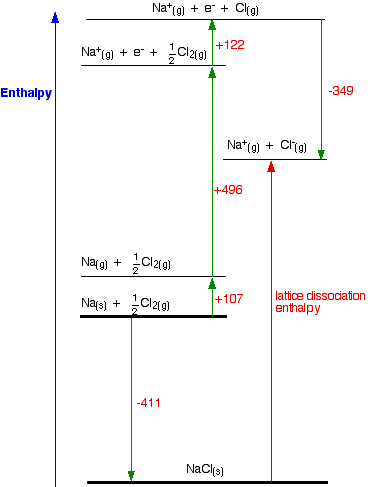
The only difference in the diagram is the direction the lattice enthalpy arrow is pointing. It does, of course, mean that you have to find two new routes. You cannot use the original one, because that would go against the flow of the lattice enthalpy arrow. This time both routes would start from the elements in their standard states, and finish at the gaseous ions.

-411 + LE = +107 + 496 + 122 - 349

LE = +107 + 496 + 122 - 349 + 411

LE = +787 kJ mol^-1

Once again, the cycle sorts out the sign of the lattice enthalpy.

Theoretical Estimates of Lattice Energies

Let's assume that a compound is fully ionic. Let's also assume that the ions are point charges - in other words that the charge is concentrated at the center of the ion. By doing physics-style calculations, it is possible to calculate a theoretical value for what you would expect the lattice energy to be. Calculations of this sort end up with values of lattice energy, and not lattice enthalpy. If you know how to do it, you can then fairly easily convert between the two.

There are several different equations, of various degrees of complication, for calculating lattice energy in this way. There are two possibilities:

• There is reasonable agreement between the experimental value (calculated from a Born-Haber cycle) and the theoretical value. Sodium chloride is a case like this - the theoretical and experimental values agree to within a few percent. That means that for sodium chloride, the assumptions about the solid being ionic are fairly good.
• The experimental and theoretical values do not agree. A commonly quoted example of this is silver chloride, AgCl. Depending on where you get your data from, the theoretical value for lattice enthalpy for AgCl is anywhere from about 50 to 150 kJ mol^-1 less than the value that comes from a Born-Haber cycle. In other words, treating the AgCl as 100% ionic underestimates its lattice enthalpy by quite a lot.

The explanation is that silver chloride actually has a significant amount of covalent bonding between the silver and the chlorine, because there is not enough electronegativity difference between the two to allow for complete transfer of an electron from the silver to the chlorine. Comparing experimental (Born-Haber cycle) and theoretical values for lattice enthalpy is a good way of judging how purely ionic a crystal is.

Example \(\PageIndex{2}\): Born-Haber Cycle for \(\ce{MgCl2}\)

The question arises as to why, from an energetics point of view, magnesium chloride is MgCl₂ rather than MgCl or MgCl₃ (or any other formula you might like to choose). It turns out that MgCl₂ is the formula of the compound which has the most negative enthalpy change of formation - in other words, it is the most stable one relative to the elements magnesium and chlorine.

Let's look at this in terms of Born-Haber cycles of and contrast the enthalpy change of formation for the imaginary compounds MgCl and MgCl₃. That means that we will have to use theoretical values of their lattice enthalpies. We ca not use experimental ones, because these compounds obviously do not exist! I'm taking theoretical values for lattice enthalpies for these compounds that I found on the web. I can't confirm these, but all the other values used by that source were accurate. The exact values do not matter too much anyway, because the results are so dramatically clear-cut.

1. The Born-Haber cycle for MgCl

We will start with the compound MgCl, because that cycle is just like the NaCl one we have already looked at.

\[ \ce{Mg(s) + 1/2 Cl_2(g) \rightarrow MgCl (s)} \nonumber \]

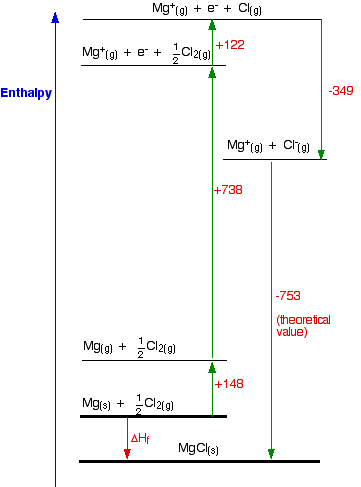
Find two routes around this without going against the flow of any arrows. That's easy:

ΔH_f = +148 + 738 + 122 - 349 - 753

ΔH_f = -94 kJ mol^-1

So the compound MgCl is definitely energetically more stable than its elements. I have drawn this cycle very roughly to scale, but that is going to become more and more difficult as we look at the other two possible formulae. So I am going to rewrite it as a table. You can see from the diagram that the enthalpy change of formation can be found just by adding up all the other numbers in the cycle, and we can do this just as well in a table.

	kJ
atomization enthalpy of Mg	+148
1st IE of Mg	+738
atomization enthalpy of Cl	+122
electron affinity of Cl	-349
lattice enthalpy	-753
calculated ΔHf	-94

2. The Born-Haber cycle for MgCl₂

The equation for the enthalpy change of formation this time is

\[ \ce{Mg (s) + Cl2 (g) \rightarrow MgCl2 (s)} \nonumber \]

So how does that change the numbers in the Born-Haber cycle?

• You need to add in the second ionization energy of magnesium, because you are making a 2+ ion.
• You need to multiply the atomization enthalpy of chlorine by 2, because you need 2 moles of gaseous chlorine atoms.
• You need to multiply the electron affinity of chlorine by 2, because you are making 2 moles of chloride ions.
• You obviously need a different value for lattice enthalpy.

	kJ
atomization enthalpy of Mg	+148
1st IE of Mg	+738
2nd IE of Mg	+1451
atomization enthalpy of Cl (x 2)	+244
electron affinity of Cl (x 2)	-698
lattice enthalpy	-2526
calculated ΔHf	-643

You can see that much more energy is released when you make MgCl₂ than when you make MgCl. Why is that? You need to put in more energy to ionize the magnesium to give a 2+ ion, but a lot more energy is released as lattice enthalpy. That is because there are stronger ionic attractions between 1- ions and 2+ ions than between the 1- and 1+ ions in MgCl. So what about MgCl₃? The lattice energy here would be even greater.

3. The Born-Haber cycle for MgCl₃

The equation for the enthalpy change of formation this time is

\[ \ce{Mg(s) + 3/2 Cl_2(g) \rightarrow MgCl_3 (s)} \nonumber \]

So how does that change the numbers in the Born-Haber cycle this time?

• You need to add in the third ionization energy of magnesium, because you are making a 3+ ion.
• You need to multiply the atomization enthalpy of chlorine by 3, because you need 3 moles of gaseous chlorine atoms.
• You need to multiply the electron affinity of chlorine by 3, because you are making 3 moles of chloride ions.
• You again need a different value for lattice enthalpy.

	kJ
atomization enthalpy of Mg	+148
1st IE of Mg	+738
2nd IE of Mg	+1451
3rd IE of Mg	+7733
atomization enthalpy of Cl (x 3)	+366
electron affinity of Cl (x 3)	-1047
lattice enthalpy	-5440
calculated ΔHf	+3949

This time, the compound is hugely energetically unstable, both with respect to its elements, and also to other compounds that could be formed. You would need to supply nearly 4000 kJ to get 1 mole of MgCl₃ to form!

Look carefully at the reason for this. The lattice enthalpy is the highest for all these possible compounds, but it is not high enough to make up for the very large third ionization energy of magnesium.

Why is the third ionization energy so big? The first two electrons to be removed from magnesium come from the 3s level. The third one comes from the 2p. That is closer to the nucleus, and lacks a layer of screening as well - and so much more energy is needed to remove it. The 3s electrons are screened from the nucleus by the 1 level and 2 level electrons. The 2p electrons are only screened by the 1 level (plus a bit of help from the 2s electrons).

Conclusion

Magnesium chloride is MgCl₂ because this is the combination of magnesium and chlorine which produces the most energetically stable compound - the one with the most negative enthalpy change of formation.

Contributors and Attributions

• Jim Clark (Chemguide.co.uk)