Non-octahedral Complexes

Learning Objectives

• Understand the d-orbital degeneracies of square planar and tetrahedral metal complexes.

Tetragonal and Square Planar Complexes

If two trans- ligands in an octahedral complex are either chemically different from the other four (as in trans-[Co(NH₃)₄Cl₂]⁺), or at a different distance from the metal than the other four, the result is a tetragonally distorted octahedral complex. The electronic structures of such complexes are best viewed as the result of distorting an octahedral complex. Consider, for example, an octahedral complex such as [Co(NH₃)₆]³⁺: two trans- NH₃ molecules are slowly removed from the metal along the ±z axes, as shown in the top half of Figure \(\PageIndex{1}\). As the two axial Co–N distances increase simultaneously, the d-orbitals that interact most strongly with the two axial ligands decrease in energy due to a decrease in electrostatic repulsions between the electrons in these orbitals and the negative ends of the ligand dipoles. The affected d orbitals are those with a component along the ±z axes—d_z², d_xz, and d_yz​. These orbitals are not affected equally, however: because the d_z² orbital points directly at the two ligands being removed, its energy will decrease much more rapidly than the degenerate energies of the d_xz and d_yz, as shown in the bottom half of Figure \(\PageIndex{1}\). In addition, the effective positive charge on the metal increases somewhat as the axial ligands are removed, increasing the attraction between the four remaining ligands and the metal. This increases the extent of their interactions with the other two d orbitals and increases their energies. Again, the two d orbitals are not affected equally: because the d_x²−y² orbital points directly at the four in-plane ligands, its energy increases to a greater extent than the energy of the d_xy orbital, which points between the in-plane ligands. If the two axial ligands are moved infinitely far away from the metal, a square planar complex is formed. The energy of the d_xy​ orbital actually surpasses that of the d_z² orbital in the process. The largest orbital splitting in a square planar complex, between the d_x²−y² and d_xy​ energy levels, is identical in magnitude to Δ_o.

Figure \(\PageIndex{1}\) d-Orbital Splittings for Tetragonal and Square Planar Complexes. (CC BY-SA-NC; anonymous by request)

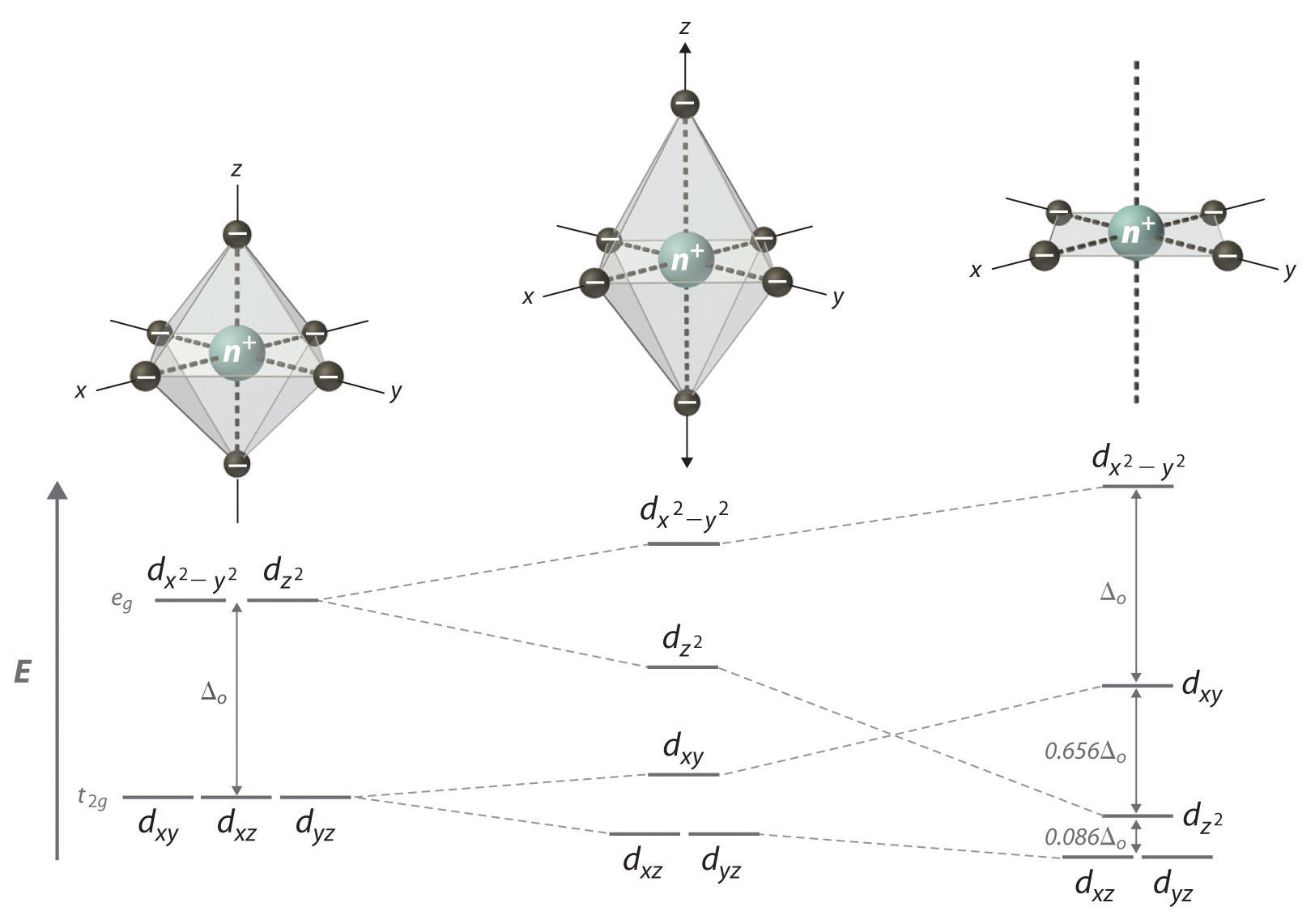
Moving the two axial ligands away from the metal ion along the z axis initially generates an elongated octahedral complex (the center compound of Figure \(\PageIndex{1}\)) and eventually produces a square planar complex (right). As shown below the structures, an axial elongation causes the d_z² d_xz and d_yz orbitals to decrease in energy and the \(d_{x^2-y^2}\) and \(d_{xy}\) orbitals to increase in energy. The change in energy is not the same for all five d orbitals. The d_z² orbital has a smaller xy component than does the d_xy orbital, so it reaches a lower energy level; thus, the order of these orbitals is reversed.

Tetrahedral Complexes

In a tetrahedral arrangement of four ligands around a metal ion, none of the ligands lies on any of the three coordinate axes (illustrated in part (a) in Figure \(\PageIndex{2}\)); consequently, none of the five d orbitals points directly at the ligands. Nonetheless, the d_xy, d_xz, and d_yz orbitals interact more strongly with the ligands than do d_x²−y² and d_z²​; this again results in a splitting of the five d orbitals into two groups. The splitting of the energies of the orbitals in a tetrahedral complex (Δ_t) is much smaller than that for an octahedral complex (Δ_o), however, for two reasons: first, the d orbitals interact less strongly with the ligands in a tetrahedral arrangement; second, there are only four negatively-charged regions rather than six, which decreases the electrostatic interactions by one-third if all other factors are equal. It can be shown that for complexes of the same metal ion with the same charge, the same ligands, and the same M–L distance, \(\Delta_\textrm t=\frac{4}{9}\Delta_\textrm o\). The relationship between the splitting of the five d orbitals in octahedral and tetrahedral crystal fields imposed by the same ligands is shown schematically in part (b) in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): d-Orbital Splittings for a Tetrahedral Complex. (a) In a tetrahedral complex, none of the five d orbitals points directly at or between the ligands. (b) Because the d_xy, d_xz, and d_yzorbitals (the t_2g orbitals) interact more strongly with the ligands than do the d_x²−y² and d_z² orbitals (the e_g orbitals), the order of orbital energies in a tetrahedral complex is the opposite of the order in an octahedral complex. (CC BY-SA-NC; anonymous by request)

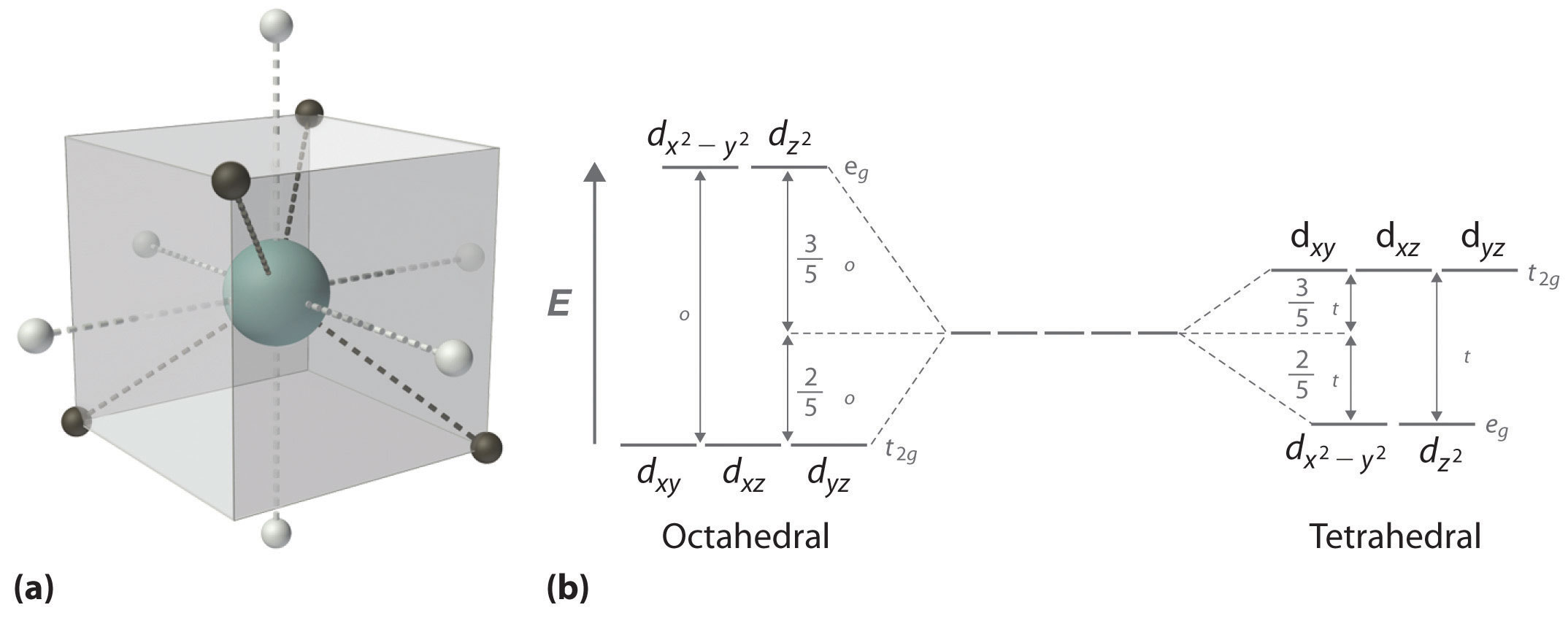
Δ_t < Δ_o because of weaker d-orbital–ligand interactions and decreased electrostatic interactions.

Example \(\PageIndex{1}\): Predicting Structure

For each complex, predict its structure, whether it is high spin or low spin, and the number of unpaired electrons present.

1. \([Cu(NH_3)_4]^{2+}\)
2. \([Ni(CN)_4]^{2−}\)

Solution

Because Δ_o is so large for the second- and third-row transition metals, all four-coordinate complexes of these metals are square planar due to the much higher crystal field stabilization energy (CFSE) for square planar versus tetrahedral structures. The only exception is for d¹⁰ metal ions such as Cd²⁺, which have zero CFSE and are therefore tetrahedral as predicted by the VSEPR model. Four-coordinate complexes of the first-row transition metals can be either square planar or tetrahedral; the former is favored by strong-field ligands, whereas the latter is favored by weak-field ligands. For example, the [Ni(CN)₄]²⁻ ion is square planar, while the [NiCl₄]²⁻ ion is tetrahedral.

1.

The copper in this complex is a d⁹ ion and it has a coordination number of 4. So it is probably either square planar or tetrahedral. To estimate which, we need to fill in the CFT splitting diagrams for each with 9 electrons and ask which has a lower energy. Comparing the square planer (Figure \(\PageIndex{1}\)) splitting diagram with tetrahedral (Figure \(\PageIndex{2}\)), suggests that 9 electrons will have a net lower total energy for square planar (since the \(d_{x^2-y^2}\) orbital is high in energy, the others are lower).

For the square planar structure, neither high nor low spin states are possible (only one state) with a single unpaired electron.

2.

The nickle in this complex is a d⁸ ion and it has a coordination number of 4. So it is probably either square planar or tetrahedral. To estimate which, we need to fill in the CFT splitting diagrams for each with 8 electrons and ask which has a lower energy. Comparing the square planer (Figure \(\PageIndex{1}\)) splitting diagram with tetrahedral (Figure \(\PageIndex{2}\)), suggests that 8 electrons will have a net lower total energy for square planar (since the \(d_{x^2-y^2}\) orbital is high in energy, the others are lower).

For the square planar structure, it is a low spin complex since a high spin requires a lot of energy to promote to the \(d_{x^2-y^2}\) orbital. Hence, there are no unpaired electrons

Exercise \(\PageIndex{1}\)

What are the geometries of the following two complexes?

1. \([\ce{AlCl_4}]^-\)
2. \([\ce{Ag(NH_3)_2}]^+\)

Answer 1

tetrahedral

Answer 2

linear

Summary

Distorting an octahedral complex by moving opposite ligands away from the metal produces a tetragonal or square planar arrangement, in which interactions with equatorial ligands become stronger. Because none of the d orbitals points directly at the ligands in a tetrahedral complex, these complexes have smaller values of the crystal field splitting energy Δ_t. In tetrahedral molecular geometry, a central atom is located at the center of four substituents, which form the corners of a tetrahedron. Tetrahedral geometry is common for complexes where the metal has \(d^0\) or \(d^{10}\) electron configuration. The CFT diagram for tetrahedral complexes has \(d_{x^2-y^2}\) and \(d_{z^2}\) orbitals equally low in energy because they are between the ligand axis and experience little repulsion. In square planar molecular geometry, a central atom is surrounded by constituent atoms, which form the corners of a square on the same plane. The square planar geometry is prevalent for transition metal complexes with d⁸ configuration. The CFT diagram for square planar complexes can be derived from octahedral complexes yet the \(d_{x^2-y^2}\) level is the most destabilized and is left unfilled.