11.11: The Fugacity and Gibbs Free Energy of A Substance in Any System
- Page ID
- 152358
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
We can find the Gibbs free energy of formation for substances whose standard states are condensed phases. As indicated in Section 11.9, we adopt the same rule for any substance; we set \(G^o_A={\Delta }_fG^o\left(A\right)\) for any substance, whether its standard state is a gas, liquid, or solid. The Gibbs free energy of the elements becomes the “zero point” for the Gibbs free energy of any substance.
In Chapters 14 and 15, we see that we can also define the fugacity of any substance in any system; that is, we can define the fugacity for a pure liquid, a pure solid, or for one component in any mixture. When we do so, the Gibbs free energy of one mole of the substance in the system, \({\overline{G}}_A\left(\mathrm{system},P\right)\), is given by the same relationship we developed for the molar Gibbs free energy of a pure gas. We find
\[{\overline{G}}_A\left(\mathrm{system},P\right)={\Delta }_fG^o_A\left({HIG}^o\right)+RT{ \ln \left(\frac{f_A\left(\mathrm{system},P\right)}{f_A\left({HIG}^o\right)}\right)\ } \nonumber \]
To obtain this result and to see how to find the fugacity of \(A\) in any system, \(f_A\left(\mathrm{system},P\right)\), we must introduce a number of additional ideas. For now, let us note some of the consequences.
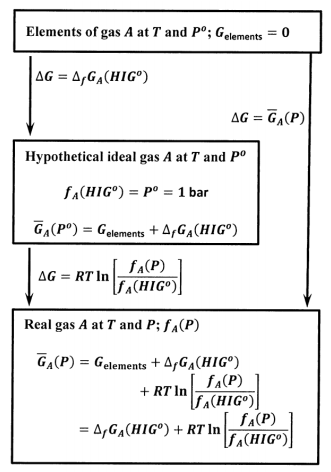
The essential consequence is that the difference between the Gibbs free energy of one mole of a substance in two different systems, say system X and system Y, can be expressed using the ratio of the corresponding fugacities. That is,
\[{\overline{G}}_A\left(\mathrm{system}\mathrm{\ \ X},P_X\right)-{\overline{G}}_A\left(\mathrm{system}\mathrm{\ \ Y},P_Y\right)=RT{ \ln \left(\frac{f_A\left(\mathrm{system},P_X\right)}{f_A\left(\mathrm{system}\mathrm{\ \ Y},P_Y\right)}\right)\ } \nonumber \]
where \(P_X\) and \(P_Y\) are the pressures of systems X and Y, respectively, and both systems are at the same temperature.
For liquids and solids, the standard state is the pure substance in its most stable form at one bar and the temperature of interest. The fugacity in the standard state must be determined experimentally. If the liquid or solid has negligible vapor pressure, this may not be possible. Since we intend “any system” to include all manner of mixtures and solutions, it can be very difficult to find the Gibbs free energy change for taking the substance from its standard state to the arbitrary system in which its fugacity is \(f_A\left(\mathrm{system},P\right)\). In Chapter 14, we introduce the chemical activity of the substance to cope with such cases.
When we define the chemical activity of a substance in a particular system, we also introduce a new standard state. The primary criterion for our choice of this activity standard state is that we be able to measure how much the Gibbs free energy of the substance differs between the activity standard state and other states of the system. A principal object of the next seven chapters is to introduce ideas for measuring the difference between the Gibbs free energy of a substance in two states of a given system. Even so, our treatment of the issues involved in this step is quite incomplete.


