11.7: The Fugacity of a Gas

As it turns out, the pressure-dependence of the Gibbs free energy is useful more often than that of the enthalpy or entropy. From the defining relationship, \(G=H-TS\), and the results above, we find

\[\begin{align*} {\Delta }_fG^o_A\left({HIG}^o\right) &={\Delta }_fH^o_A\left({HIG}^o\right)-T{\Delta }_fS^o_A\left({HIG}^o\right) \\[4pt] &={\overline{H}}_A\left(P\right)+\int^{P^*}_P{\left[\overline{V}-T{\left(\frac{\partial \overline{V}}{\partial T}\right)}_P\right]dP} -T{\overline{S}}_A\left(P\right)+\int^{P^*}_P{T{\left(\frac{\partial \overline{V}}{\partial T}\right)}_PdP}+\int^{P^o}_{P^*}{\frac{RT}{P}dP} \\[4pt] &={\overline{G}}_A\left(P\right)-\int^P_{P^*}{\overline{V}dP}-\int^{P^*}_{P^o}{\frac{RT}{P}dP} \end{align*} \]

where we have reversed the direction of integration in the remaining integrals. Again, we cannot evaluate the integrals with \(P^* = 0\). To overcome this difficulty, we introduce a clever expedient: we add and subtract the same integral, obtaining

\[{\Delta }_fG^o_A\left({HIG}^o\right)={\overline{G}}_A\left(P\right)-\int^P_{P^*}{\overline{V}dP}-\int^{P^*}_{P^o}{\frac{RT}{P}dP} \nonumber \] \[-\int^P_{P^*}{\frac{RT}{P}dP}+\int^P_{P^*}{\frac{RT}{P}dP} \nonumber \]

\[ ={\overline{G}}_A\left(P\right)-\int^P_{P^*}{\left[\overline{V}-\frac{RT}{P}\right]dP}-\int^P_{P^o}{\frac{RT}{P}dP} \nonumber \]

This result is pivotal. We will derive it again later by a slightly different argument. For now, we evaluate the last integral and rearrange the equation to the form in which we write it most often:

\[{\overline{G}}_A\left(P\right)={\Delta }_fG^o_A\left({HIG}^o\right)+RT{ \ln \left(\frac{P}{P^0}\right)\ }+RT\int^P_0{\left[\frac{\overline{V}}{RT}-\frac{1}{P}\right]dP} \nonumber \]

In doing so, we use the fact that

\[\frac{\overline{V}}{RT}-\frac{1}{P} \nonumber \]

vanishes for any gas when the pressure is sufficiently low, which means that the integral from \(P^*\)to \(P\) remains finite when we let \(P^*\to 0\).

Recapitulating: The last equation relates the Gibbs free energy of one mole of a real gas at pressure \(P\) and temperature \(T\), \({\overline{G}}_A\left(P\right)\), to the Gibbs free energy of formation of the gas in its standard state, \({\Delta }_f\)\(G^o_A\left({HIG}^o\right)\), where the standard state is the hypothetical ideal gas at \(P=P^o=1\ \mathrm{bar}\) and the same temperature. (We write “\(RT{ \ln \left({P}/{P^o}\right)\ }\)” rather than “\(RT{ \ln P\ }\)” to emphasize that the argument of the logarithm is a dimensionless quantity.)

If the gas is ideal, the integrand is zero at any pressure. For an ideal gas, the Gibbs free energy, at pressure \(P\) and temperature \(T\), is related to the Gibbs free energy in the standard state by

\[{\overline{G}}_A\left(P\right)=G^o_A\left(\mathrm{1\ bar}\right)+RT{ \ln \left(\frac{P}{P^o}\right)\ } \nonumber \] (ideal gas)

This observation enables us to give a physical interpretation to the integral

\[\int^P_0{\left[\overline{V}-\frac{RT}{P}\right]dP}=RT\int^P_0{\left[\frac{\overline{V}}{RT}-\frac{1}{P}\right]dP} \nonumber \]

Evidently, this integral is the difference between the Gibbs free energy of one mole of the real gas and the Gibbs free energy that it would have if it behaved as an ideal gas. When we add it to the Gibbs free energy of the hypothetical ideal gas, we get the Gibbs free energy of the real gas.

For an ideal gas, the Gibbs free energy is a simple function of its pressure. It turns out to be useful to view the integral as a contribution to a “corrected pressure.” The “correction” is an adjustment to the pressure that, in our calculations, makes the real gas behave as an ideal gas. The idea is that we can express the Gibbs free energy as a function of this corrected pressure, which we call the fugacity, and to which we give the symbol “\(f\) ”. Fugacity is therefore a function of pressure. Fugacity also has the units of pressure, which we always take to be bars. We define the fugacity of \(A\) at pressure \(P\), \(f_A\left(P\right)\), by

\[{\overline{G}}_A\left(P\right)={\Delta }_fG^o_A\left({HIG}^o\right)+RT{ \ln \left(\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right)\ } \nonumber \] (real gas)

The fugacity, \(f_A\left({HIG}^o\right)\), and the standard Gibbs free energy of formation, \({\Delta }_fG^o_A\left({HIG}^o\right)\), describe the same state. We define the fugacity in this standard state to be one bar. That is, the fugacity of a substance in its hypothetical ideal-gas standard state, \(f_A\left({HIG}^o\right)\), is a constant whose value is 1 bar. (If we want to express fugacity in units of, say, pascals, then \(P^o=f_A\left({HIG}^o\right)={10}^5\ \mathrm{Pa}\).)

We can calculate the fugacity of a real gas, at pressure \(P\) and temperature \(T\), from

\[RT{ \ln \left(\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right)\ }=\ RT{ \ln \left(\frac{P}{P_0}\right)\ }+RT\int^P_0{\left[\frac{\overline{V}}{RT}-\frac{1}{P}\right]dP} \nonumber \]

We find it useful to introduce a function of pressure that we call the fugacity coefficient, \({\gamma }_A\left(P\right)\). We define it as

\[{\gamma }_A\left(P\right)=\frac{f_A\left(P\right)}{P} \nonumber \]

Since \(f_A\left({HIG}^o\right)=P^o=1\ \mathrm{bar}\), we have

\[{ \ln {\gamma }_A\left(P\right)\ }=\int^P_0{\left[\frac{\overline{V}}{RT}-\frac{1}{P}\right]dP} \nonumber \]

Figure 3. Graphical description of \(\ln \gamma\)

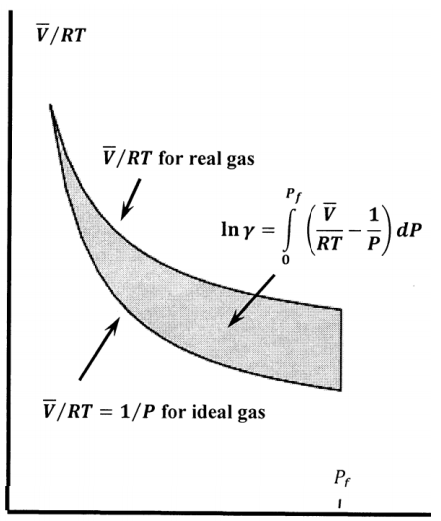
Figure 3 exhibits these quantities graphically. The shaded area is \({ \ln {\gamma }_A\left(P\right)\ }\).