9.1: The Second Law of Thermodynamics

The first law of thermodynamics is concerned with energy and its properties. As we saw in Chapter 7, the first law arose from the observation that the dissipation of mechanical work through friction creates heat. In a synthesis that was partly definition and partly a generalization from experience, it was proposed that mechanical energy and heat are manifestations of a common quantity, energy. Later, by further definition and generalization, the concept was expanded to include other forms of energy. The energy concept evolved into the prescript that there exists a quantity (state function) that is conserved through any manner of change whatsoever.

The element of definition arises from the fact that we recognize new forms of energy whenever necessary in order to ensure that the conservation condition is satisfied. The element of experience arises from the fact that this prescript has resulted in a body of theory and a body of experimental results that are mutually compatible. When we define and measure energy “correctly” we do indeed find that energy is a state function and that it is conserved.

The theory of relativity introduced a significant expansion of the energy concept. For chemical processes, we can view mass and energy conservation as independent postulates. For processes in which fundamental particles undergo changes and for systems moving at velocities near that of light, we cannot. Relativity asserts that the energy of a particle is given by Einstein’s equation,

\[E^2=p^2c^2+m^2_0c^4. \nonumber \]

In this equation, \(E\) is the particle energy, \(p\) is its momentum, \(m_0\) is its rest mass, and \(c\) is the speed of light. In transformations of fundamental particles in which the sum of the rest masses of the product particles is less than that of the reactant particles, conservation of energy requires that the sum of the momenta of the product particles exceed that of the reactant particles. The momentum increase means that the product particles have high velocities, corresponding to a high temperature for the product system. The most famous expression of this result is that \(E=m_0c^2\), meaning that we can associate this quantity of energy with the mass, \(m_0\), of a stationary particle, for which \(p=0\).

The situation with respect to the second law is similar. From experience with devices that convert heat into work, the idea evolved that such devices must have particular properties. Consideration of these properties led to the discovery of a new state function, which we call entropy, and to which we customarily assign the symbol “\(S\)”. We introduce the laws of thermodynamics in §6-13. We repeat our statement of the second law here:

The Second Law of Thermodynamics

In a reversible process in which a closed system accepts an increment of heat, \(\boldsymbol{d}\boldsymbol{q}^\boldsymbol{rev}\), from its surroundings, the change in the entropy of the system, \(\boldsymbol{dS}\), is \(\boldsymbol{dS}\boldsymbol{=}\boldsymbol{dq}^\boldsymbol{rev}/\boldsymbol{T}\). Entropy is a state function. For any reversible process, \(\boldsymbol{dS}_\boldsymbol{universe}\boldsymbol{=}\boldsymbol{0}\), and conversely. For any spontaneous process, \(\boldsymbol{dS}_\boldsymbol{universe}\boldsymbol{>}\boldsymbol{0}\), and conversely.

If a spontaneous process takes a system from state A to state B, state B may or may not be an equilibrium state. State A cannot be an equilibrium state. Since we cannot use the defining equation to find the entropy change for a spontaneous process, we must use some other method if we are to estimate the value of the entropy change. This means that we must have either an empirical mathematical model from which we can estimate the entropy of a non-equilibrium state or an equilibrium system that is a good model for the initial state of the spontaneous process.

We can usually find an equilibrium system that is a good model for the initial state of a spontaneous process. Typically, some alteration of an equilibrium system makes the spontaneous change possible. The change-enabled state is the initial state for a spontaneous process, but its thermodynamic state functions are essentially identical to those of the pre-alteration equilibrium state. For example, suppose that a solution contains the reactants and products for some reaction that occurs only in the presence of a catalyst. In this case, the solution can be effectively at equilibrium even when the composition does not correspond to an equilibrium position of the reaction. (In an effort to be more precise, we can term this a quasi-equilibrium state, by which we mean that the system is unchanging even though a spontaneous change is possible.) If we introduce a very small quantity of catalyst, and consider the state of the system before any reaction occurs, all of the state functions that characterize the system must be essentially unchanged. Nevertheless, as soon as the catalyst is introduced, the system can no longer be considered to be in an equilibrium state. The spontaneous reaction proceeds until it reaches equilibrium. We can find the entropy change for the spontaneous process by finding the entropy change for a reversible process that takes the initial, pre-catalyst, quasi-equilibrium state to the final, post-catalyst, equilibrium state.

Our statement of the second law establishes the properties of entropy by postulate. While this approach is rigorously logical, it does not help us understand the ideas involved. Like the first law, the second law can be stated several ways. To develop our understanding of entropy and its properties, it is useful to again consider a more traditional statement of the second law:

A Traditional statement of the second law

It is impossible to construct a machine that operates in a cycle, exchanges heat with its surroundings at only one temperature, and produces work in the surroundings.

When we introduce the qualification that the machine “exchanges heat with its surroundings at only one temperature,” we mean that the temperature of the surroundings has a particular value whenever the machine and surroundings exchange heat. The statement does not place any conditions on the temperature of the machine at any time.

In this chapter, we have frequent occasion to refer to each of these statements. To avoid confusing them, we will refer to our statement of the second law as the entropy-based statement. We will refer to the statement above as the machine-based statement of the second law.

By “a machine”, we mean a heat engine—a device that accepts heat and produces mechanical work. This statement asserts that a “perpetual motion machine of the second kind” cannot exist. Such a machine accepts heat energy and converts all of it into work, while itself returning to the same state at the end of each cycle. (In §7-11, we note that a “perpetual motion machine of the first kind” is one whose operation violates the principle of conservation of energy.) Normally, we view this statement as a postulate. We consider that we infer it from experience. Unlike our statements about entropy, which are entirely abstract, this statement makes an assertion about real machines of the sort that we encounter in daily life. We can understand the assertion that it makes in concrete terms: A machine that could convert heat from a constant-temperature source into work could extract heat from ice water, producing ice cubes in the water and an equivalent amount of work elsewhere in the surroundings. This machine would not exchange heat with any other heat reservoir. Our machine-based statement of the second law postulates that no such machine can exist.

Our entropy-based statement of the second law arose from thinking about the properties of machines that do convert heat into work. We trace this thinking to see how our entropy-based statement of the second law was developed. Understanding this development gives us a better appreciation for the meaning of entropy. We find that we must supplement the machine-based statement of the second law with additional assumptions in order to arrive at all of the properties of the entropy function that are asserted in the entropy-based statement.

However, before we undertake to develop the entropy-based statement of the second law from the machine-based statement, let us develop the converse; that is, let us show that the machine-based statement is a logical consequence of the entropy-based statement. To do so, we assume that a perpetual motion machine of the second kind is possible. To help keep our argument clear, let proposition \(\mathrm{MSL}\) be the machine-based statement. We are assuming that proposition \(\mathrm{MSL}\) is false, so that proposition \(\sim \mathrm{MSL}\) is true. We let \(\mathrm{SL}\) be the entropy-based statement of the second law.

The sketch in Figure 1 describes the interaction of this perpetual motion machine, \(\mathrm{PPM}\), with its surroundings. From our entropy-based statement of the second law, we can assert some important facts about the entropy changes that accompany operation of the machine. Since entropy is a state function, \(\Delta S=0\) for one cycle of the machine. If the machine works (that is, \(\sim \mathrm{MSL}\) is true), then the entropy-based statement requires that \(\Delta S_{universe}=\Delta S+\Delta \hat{S}\ge 0\). Since \(\Delta S=0\), it follows that \(\Delta \hat{S}\ge 0\). We can make this more explicit by writing: \(\left(\mathrm{SL\ and}\ \sim \mathrm{MSL}\right)\Rightarrow \Delta \hat{S}\ge 0\).

The machine-based statement of the second law also enables us to determine the entropy change in the surroundings from our second-law definition of entropy. In one cycle, this machine (system) delivers net work, \(\hat{w}>0\), to the surroundings; it accepts a net quantity of heat, \(q>0\), from the surroundings, which are at temperature, \(\hat{T}\). Simultaneously, the surroundings surrender a quantity of heat, \(\hat{q}\), where \(\hat{q}=-q\), and \(\hat{q}<0\). The change that occurs in one cycle of the machine need not be reversible. However, whether the change is reversible or not, the entire thermal change in the surroundings consists in the exchange of an amount of heat, \(\hat{q}<0\), by a constant temperature reservoir at \(\hat{T}\). We can effect identically the same change in the surroundings using some other process to reversibly extract this amount of heat. The entropy change in the surroundings in this reversible process will be \({\hat{q}}/{\hat{T}}\), and this will be the same as the entropy change for the surroundings in one cycle of the machine. (We consider this conclusion further in §15.) It follows that \(\Delta \hat{S}={\hat{q}}/{\hat{T}}\), and since \(\hat{q}<0\), while \(\hat{T}>0\), we have \(\Delta \hat{S}<0\). We can write this conclusion more explicitly: \(\left(\mathrm{SL\ and}\ \sim \mathrm{MSL}\right)\Rightarrow \Delta \hat{S}<0\).

Figure 1. A perpetual motion machine (PPM) that violates the second law.

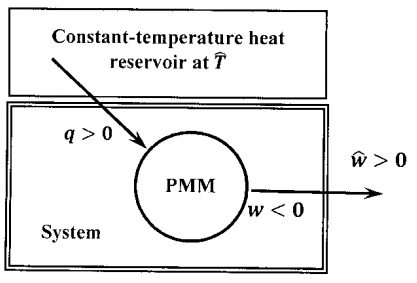
By assuming a perpetual motion machine of the second kind is possible—that is, by assuming \(\sim \mathrm{MSL}\) is true—we derive the contradiction that both \(\Delta \hat{S}\ge 0\) and \(\Delta \hat{S}<0\). Therefore, proposition \(\sim \mathrm{MSL}\) must be false. Proposition \(\mathrm{MSL}\) must be true. The entropy-based second law of thermodynamics implies that a perpetual motion machine of the second kind is not possible. That is, the entropy-based statement of the second law implies the machine-based statement. (We prove that \(\sim \left(\mathrm{SL\ and}\ \sim \mathrm{MSL}\right)\); it follows that \(\mathrm{SL\ }\mathrm{\Rightarrow }\mathrm{MSL}\). For a more detailed argument, see problem 2.)