4.16: The Energy of A Collision between Gas Molecules
- Page ID
- 151999
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
It is useful to extend our model of molecular collisions to suppose that one or both of the molecules can undergo chemical change as a result of the collision. In doing so, we are introducing some ideas that we develop further in Chapter 5.
When we ask about the factors that determine whether such a reaction can occur, there can be several possibilities. We want to focus on one such factor—the violence of the collision. We expect that a collision is more likely to result in a reaction the harder the two molecules hit one another. When we try to formulate our basis for this expectation, we see that the underlying idea is that a collision deforms the colliding molecules. The more violent the collision, the greater the deformation, and the greater the likelihood of reaction becomes.
To proceed, we need to be more precise about what we mean by the violence of the collision. Evidently, what we have in mind has two components: the relative velocity and the collision angle. If the collision is a glancing one, \(\theta ={\pi }/{2}\), we expect the effect on the molecules to be minimal, even if the relative velocity is high. On the other hand, a direct collision, \(\theta \approx 0\), might lead to reaction even if the relative velocity is comparatively low. With these ideas in mind, we see that a reasonable model is to suppose that forces acting along the line of centers can lead to reaction, whereas forces acting perpendicular to the line of centers cannot. If the colliding molecules have complex shapes, this may be a poor assumption.
We also need a way to specify how much deformation occurs in a collision. If we want to specify the deformation by describing specific changes in the molecular structures, this is a complex problem. For a general model, however, we can avoid this level of detail. To do so, we recognize that any deformation can proceed only until the work done in deforming the molecules equals the energy that can be expended to do this work. As the molecules are deformed, their potential energies change. The maximum change in this potential energy is just the amount of kinetic energy that the colliding molecules can use to effect this deformation. We can identify this amount of kinetic energy with the component of the molecules’ kinetic energy that is associated with their relative motion along the line of centers.
If we now associate a threshold level of deformation with the occurrence of a chemical change, the kinetic energy required to effect this deformation determines whether the change can occur. If the available kinetic energy is less than that required to achieve the threshold level of deformation, reaction cannot occur. If the available kinetic energy exceeds this minimum, reaction takes place. We call the minimum kinetic energy the activation energy and usually represent it by the symbol \({\epsilon }_a\). (In discussing reaction rates, we usually express the activation energy per mole and represent it as \(E_a\), where \[E_a=\overline{N}{\epsilon }_a.) \nonumber \]
We can apply these ideas to our model for collision between spherical molecules. In Section 4.10, we develop relative velocity coordinates. It follows that we can partition kinetic energy of the two-particle system into a component that depends on the velocity of the center of mass and a component that depends on the relative velocity. That is, we have
\[ \begin{aligned} KE & =\frac{m_1v^2_1}{2}+\frac{m_2v^2_2}{2} \\ & =\frac{m_1m_2}{2\mu }\left(\dot{x}^2_0+\dot{y}^2_0+z^2_0\right)+\mu \left(\dot{x}^2_{12}+\dot{y}^2_{12}+\dot{z}^2_{12}\right) \\ & =\frac{m_1m_2v^2_0}{2\mu }+\frac{\mu v^2_{12}}{2} \end{aligned} \nonumber \]
Only the component that depends on the relative velocity can contribute to the deformation of the colliding molecules. The relative velocity can be resolved into components parallel and perpendicular to the line of centers. The parallel component is the projection of the velocity vector onto the line of centers. This is \(v_{12} \mathrm{cos} \theta\), and the perpendicular component is \(v_{12}\mathrm{sin} \theta\). We see that the kinetic energy associated with the relative motion of particles 1 and 2 has a component
\[\frac{\mu v^2_{12} \mathrm{cos}^2 \theta}{2} \nonumber \]
parallel to the line of centers and a component
\[\frac{\mu v^2_{12} \mathrm{sin}^2 \theta}{2} \nonumber \]
perpendicular to it.
The idea that the kinetic energy parallel to the line of centers must exceed \({\varepsilon }_a\) for reaction to occur can now be expressed as the requirement that
\[{\epsilon }_a<\frac{\mu v^2_{12} \mathrm{cos}^2 \theta}{2} \nonumber \]
When we consider all possible collisions between molecules 1 and 2, the collision angle varies from 0 to \({\pi }/{2}\). However, only those collisions for which \(v_{12}\) satisfies the inequality above will have sufficient kinetic energy along the line of centers for reaction to occur. The smallest value of \(v_{12}\) that can satisfy this inequality occurs when \(\theta =0\). This minimum relative velocity is
\[v^{minimun}_{12}= \left(2{\epsilon }_a/{\mu }\right)^{1/2} \nonumber \]
For relative velocities in excess of this minimum, collisions are effective only when
\[\mathrm{cos} \theta > \left(2{\epsilon }_a/ \mu v^2_{12}\right)^{1/2} \nonumber \]
so that
\[\theta < \mathrm{cos}^{-1} \left(2{\epsilon }_a/\mu v^2_{12}\right)^{1/2} \nonumber \]
Let us designate the frequency of collisions satisfying these constraints as \(\widetilde{\nu }_{12}\left({\epsilon }_a\right)\). Recalling that
\[d\widetilde{\nu }_{12}\left({\nu }_{12},\theta \right)= 8{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}v^3_{12} \mathrm{exp}\left(\frac{-\mu v^2_{12}}{2kT}\right) \times \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta dv_{12} \nonumber \]
we see that
\[\widetilde{\nu }_{12}\left({\varepsilon }_a\right)=8{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2} \times \int^{\infty }_{v_{12}=\left(2{\epsilon }_a/{\mu }\right)^{1/2}} \int^{\mathrm{cos}^{-1} \left(2{\epsilon }_a/ \mu v^2_{12}\right)^{1/2}}_{\theta =0} v^3_{12}\mathrm{\ exp}\left(\frac{-\mu v^2_{12}}{2kT}\right) \times \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta dv_{12} \nonumber \]
The integral involving \(\theta\) is
\[\int^{\mathrm{cos}^{-1} \left( 2{\epsilon }_a/\mu v^2_{12}\right)^{1/2}}_{\theta =0} \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta = \left[\frac{\mathrm{sin}^2 \theta}{2}\right]^{\mathrm{cos}^{-1} \left(2{\epsilon }_a/\mu v^2_{12}\right)^{1/2}}_0=\frac{1}{2}\left[1-\frac{2{\epsilon }_a}{\mu v^2_{12}}\right] \nonumber \]
where, to evaluate the integral at its upper limit, we note that the angle \(\theta ={{\mathrm{cos}}^{-1} {\left({2{\epsilon }_a}/{\mu v^2_{12}}\right)}^{{1}/{2}}\ }\) lies in a triangle whose sides have lengths as indicated in Figure 14.
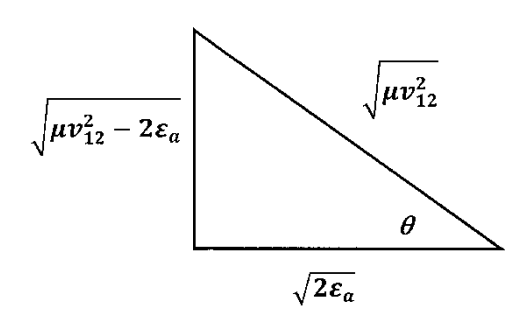
The collision frequency becomes
\[\widetilde{\nu }_{12}\left({\epsilon }_a\right)=4{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3}/{2}\times \int^{\infty }_{v_{12}=\left(2{\epsilon }_a/{\mu }\right)^{1/2}} \left[1-\frac{2{\epsilon }_a}{\mu v^2_{12}}\right]v^3_{12}\ \mathrm{exp}\left(\frac{-\mu v^2_{12}}{2kT}\right)dv_{12} \nonumber \]
This integral can be evaluated by making the substitution \(v_{12}= \left({2\epsilon }/{\mu }\right)^{1/2}\). The lower limit of integration becomes \({\epsilon }_a\); we have
\[ \begin{aligned} \int^{\infty }_{v_{12}=\left(2{\epsilon }_a/{\mu }\right)^{1/2}} & \left[1-\frac{2{\epsilon }_a}{\mu v^2_{12}}\right]v^3_{12}\ \mathrm{exp}\left(\frac{-\mu v^2_{12}}{2kT}\right)dv_{12} \\ & =\frac{2}{{\mu }^2}\int^{\infty }_{{\epsilon }_a} \left(\epsilon -{\epsilon }_a\right)\mathrm{exp}\left(\frac{-\epsilon }{kT}\right)d\epsilon \\ & =2 \left(\frac{kT}{\mu }\right)^2\mathrm{exp}\left(\frac{-{\epsilon }_a}{kT}\right) \end{aligned} \nonumber \]
Then
\[\begin{aligned} \widetilde{\nu }_{12}\left({\varepsilon }_a\right) & =4{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}\times 2 \left(\frac{kT}{\mu }\right)^2\mathrm{exp}\left(\frac{-{\epsilon }_a}{kT}\right) \\ & =N_2{\sigma }^2_{12} \left(\frac{8\pi kT}{\mu }\right)^{1/2}\mathrm{exp}\left(\frac{-{\epsilon }_a}{kT}\right) \end{aligned} \nonumber \]
Note that when \({\epsilon }_a=0\), this reduces to the same expression for \(\widetilde{\nu }_{12}\) that we have obtained twice previously. The frequency of collisions having kinetic energy along the line of centers in excess of \({\epsilon }_a\) depends exponentially on \(-{\epsilon }_a/{kT}\). All else being equal, this frequency increases as the temperature increases; it decreases as the activation energy increases.


