22.5.2: ii. Problems
- Page ID
- 84792
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Q1
Consider an interaction or perturbation which is carried out suddenly (instantaneously, e.g., within an interval of time ∆t which is small compared to the natural period \(\omega_{nm}^{-1}\) corresponding to the transition from state m to state n), and after that is turned off adiabatically (i.e., extremely slowly as V \(e^{\eta}t\)). The transition probability in this case is given as:
\[ T_{nm} \approx \dfrac{|\langle n|V|m \rangle |^2}{\hbar^2\omega_{nm}^2} \nonumber \]
where V corresponds to the maximum value of the interaction when it is turned on. This formula allows one to calculate the transition probabilities under the action of sudden perturbations which are small in absolute value whenever perturbation theory is applicable. Let's use this "sudden approximation" to calculate the probability of excitation of an electron under a sudden change of the charge of the nucleus. Consider the reaction:
\[ ^3_1H \rightarrow ^3_2He^+ + e^-, \nonumber \]
and assume the tritium atom has its electron initially in a 1s orbital.
a. Calculate the transition probability for the transition 1s → 2s for this reaction using the above formula for the transition probability.
b. Suppose that at time t = 0 the system is in a state which corresponds to the wavefunction \(\varphi_m\), which is an eigenfunction of the operator \(H_0\). At t = 0, the sudden change og the Hamiltonian occurs (now denoted as H and remains unchanged). Calculate the same 1s → 2s transition probability as in part a., only this time as the square of the magnitude of the coefficient, \(A_{1s,2s}\) using the expansion:
\[ \Psi (r,0) = \varphi_m(r) = \sum\limits_n A_{nm}\psi_n(r) \text{, where } A_{nm} = \int \varphi_m(r)\psi_n(r)d^3r \nonumber \]
Note, that the eigenfunctions of H are \(\psi_n\) with eigenvalues \(E_n\). Compare this "exact" value with that obtained by perturbation theory in part a.
Q2
The methyl iodide molecule is studied using microwave (pure rotational) spectroscopy. The following integral governs the rotational selection rules for transitions labeled J, M, K → J', M', K':
\[ I = \langle D^{J'}_{M'K'} |\vec{\epsilon}\cdot{\vec{\mu}}|D^{J}_{MK} \rangle . \nonumber \]
The dipole moment \(\vec{\mu}\) lies along the molecule's \(C_3\) symmetry axis. Let the electric field of the light \(\vec{\varepsilon}\) define the lab-fixed Z-direction.
a. Using the fact that Cos\(\beta = D^{1*}_{00}\), show that
\[ I = 8\pi^2\mu\epsilon(-1)^{(M+K)} \begin{pmatrix} J' & 1 & J \\ M & 0 & M \end{pmatrix}\begin{pmatrix} J' & 1 & J \\ K & 0 & K \end{pmatrix}\delta_{M'M}\delta_{K'K} \nonumber \]
b. What restrictions does this result place on \(\Delta J = J' - J?\) Explain physically why the K quantum number can not change.
Q3
Consider the molecule BO.
a. What are the total number of possible electronic states which can be formed by combination of ground state B and O atoms?
b. What electron configurations of the molecule are likely to be low in energy? Consider all reasonable orderings of the molecular orbitals. What are the states corresponding to these configurations?
c. What are the bond orders in each of these states?
d. The true ground state of BO is \(^2\sum\). Specify the +/- and u/g symmetries for this state.
e. Which of the excited states you derived above will radiate to the \(^2\sum\) ground state? Consider electric dipole, magnetic dipole, and electric quadrupole radiation.
f. Does ionization of the molecule to form a cation lead to a stronger, weaker, or equivalent bond strength?
g. Assuming that the energies of the molecular orbitals do not change upon ionization, what are the ground state, the first excited state, and the second excited state of the positive ion?
h. Considering only these states, predict the structure of the photoelectron spectrum you would obtain for ionization of BO.
Q4
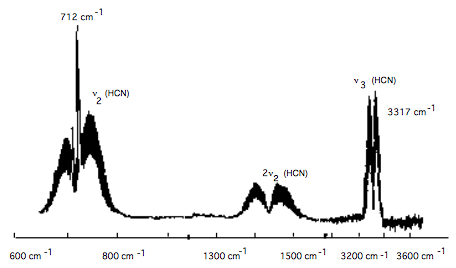
The above figure shows part of the infrared absorption spectrum of HCN gas. The molecule has a CH stretching vibration, a bending vibration, and a CN stretching vibration.
a. Are any of the vibrations of linear HCN degenerate?
b. To which vibration does the group of peaks between 600 \(\text{cm}^{-1}\) and 800 \(\text{cm}^{-1}\) belong?
c. To which vibration does the group of peaks between 3200 \(\text{cm}^{-1}\) and 3400 \(\text{cm}^{-1}\) belong?
d. What are the symmetries \((\sigma, \pi, \delta)\) of the CH stretch, CN stretch, and bending vibrational motions?
e. Starting with HCN in its 0,0,0 vibrational level, which fundamental transitions would be infrared active under parallel polarized light (i.e., z-axis polarization):
i. 000 → 001?
ii. 000 → 100?
iii. 000 → 010?
f. Which transitions would be active when perpendicular polarized light is used?
g. Why does the 712 \(\text{cm}^{-1}\) transition have a Q-branch, whereas that near 3317 \(\text{cm}^{-1}\) has only P- and R-branches?


