22.1.6: vi. Exercise Solutions
- Page ID
- 75033
Q1
- \( \begin{align} K.E. &= \dfrac{mv^2}{2} = \left( \dfrac{m}{m} \right) \dfrac{dmv^2}{2} = \dfrac{(mv)^2}{2m} = \dfrac{p^2}{2m} \\ K.E. &= \dfrac{1}{2m} \left( p_x^2 + p_y^2 + p_z^2 \right) \\ K.E. &= \dfrac{1}{2m} \left[ \left( \hbar\dfrac{\partial}{\partial x} \right)^2 + \left( \dfrac{\hbar}{i}\dfrac{\partial}{\partial y} \right)^2 + \left( \dfrac{\hbar}{i}\dfrac{\partial}{\partial z} \right)^2 \right] \\ K.E. &= \dfrac{-\hbar^2}{2m} \left[ \dfrac{\partial^2 }{\partial x^2} + \dfrac{\partial^2}{\partial y^2} \dfrac{\partial^2 }{\partial z^2} \right] \end{align} \)
- \( \begin{align} \textbf{p} &= m\textbf{v} = \textbf{i}p_x + \textbf{j}p_y + \textbf{k}p_z \\ p &= \left[ \textbf{i} \left( \dfrac{\hbar}{i}\dfrac{\partial}{\partial x} + \textbf{j} \left( \dfrac{\hbar}{i}\dfrac{\partial}{\partial y} \right) + \left( \dfrac{\hbar}{i}\dfrac{\partial}{\partial z} \right) \right) \right] \end{align} \) where i, j, and k are unit vectors along the x, y, and z axes.
- \( \begin{align} L_y &= zp_x - xp_z \\ L_y &= z \left( \dfrac{\hbar}{i}\dfrac{\partial}{\partial x} \right) - x \left( \dfrac{\hbar}{i}\dfrac{\partial}{\partial z} \right) \end{align} \)
Q2
First derive the general formulas for \( \dfrac{\partial }{\partial x}, \dfrac{\partial }{\partial y}, \dfrac{\partial }{\partial z} \) in terms of r, \(\theta \text{, and } \phi \text{, and } \dfrac{\partial }{\partial r} , \dfrac{\partial }{\partial \theta } \text{, and } \dfrac{\partial }{\partial \phi}\) in terms of x,y, and z. The general relationships are as follows:
\[ \begin{align} x &= r\sin \theta \cos \phi & r^2 &= x^2 y^2 + z^2 \\ y &= r\sin \theta \sin \phi & \sin \theta &=\dfrac{\sqrt{x^2 + y^2}}{\sqrt{x^2 + y^2 + z^2}} \\ z &= r\cos \theta & \cos \theta &= \dfrac{z}{\sqrt{x^2 + y^2 +z^2}} \\ & & \tan \phi &= \dfrac{y}{x} \end{align} \nonumber \]
First \(\dfrac{\partial }{\partial x}, \dfrac{\partial }{\partial y}\text{, and } \dfrac{\partial }{\partial z}\) from the chain rule:
\[ \begin{align} \dfrac{\partial }{\partial x} &= \left( \dfrac{\partial r}{\partial x} \right)_{y,z} \dfrac{\partial }{\partial r} + \left( \dfrac{\partial \theta }{\partial x} \right)_{y,z} \dfrac{\partial }{\partial \theta } + \left( \dfrac{\partial \phi}{\partial x} \right)_{y,z}\dfrac{\partial }{\partial \phi}, \\ \dfrac{\partial }{\partial y} &= \left( \dfrac{\partial r}{\partial y} \right)_{y,z} \dfrac{\partial }{\partial r} + \left( \dfrac{\partial \theta }{\partial y} \right)_{y,z} \dfrac{\partial }{\partial \theta } + \left( \dfrac{\partial \phi}{\partial y} \right)_{y,z}\dfrac{\partial }{\partial \phi}, \\ \dfrac{\partial }{\partial z} &= \left( \dfrac{\partial r}{\partial z} \right)_{y,z} \dfrac{\partial }{\partial r} + \left( \dfrac{\partial \theta }{\partial z} \right)_{y,z} \dfrac{\partial }{\partial \theta } + \left( \dfrac{\partial \phi}{\partial z} \right)_{y,z}\dfrac{\partial }{\partial \phi}, \\ \end{align} \nonumber \]
Evaluation of the many "coefficients" gives the following:
\[ \begin{align} \left( \dfrac{\partial r}{\partial x} \right)_{y,z} &= \sin \theta \cos \phi , & \left( \dfrac{\partial \theta }{\partial x} \right)_{y,z} &= \dfrac{\cos \theta \cos \phi}{r}, & \left( \dfrac{\partial \phi}{\partial x} \right)_{y,z} =& -\dfrac{\sin \phi}{r\sin \theta } \\ \left( \dfrac{\partial r}{\partial y} \right)_{x,z} &= \sin \theta \sin \phi , & \left( \dfrac{\partial \theta }{\partial y} \right)_{x,z} &= \dfrac{\cos \theta \sin \phi}{r}, & \left( \dfrac{\partial \phi}{\partial y} \right)_{x,z} =& \dfrac{\cos \phi}{r\sin \theta } \\ \left( \dfrac{\partial r}{\partial z} \right)_{x,z} &= \cos \theta , & \left( \dfrac{\partial \theta }{\partial z} \right)_{x,y} &= -\dfrac{\sin \theta}{r}\text{, and } & \left( \dfrac{\partial \phi}{\partial z} \right)_{y,z} =& 0. \end{align} \nonumber \]
Upon substitution of these "coefficients":
\[ \begin{align} \dfrac{\partial }{\partial x} &= \sin \theta \cos \phi\dfrac{\partial }{\partial r} + \dfrac{\cos \theta \cos \phi }{r}\dfrac{\partial }{\partial \theta } - \dfrac{\sin \phi}{r\sin \theta }\dfrac{\partial }{\partial \phi}, \\ \dfrac{\partial }{\partial y} &= \sin \theta \sin \phi\dfrac{\partial }{\partial r} + \dfrac{\cos \theta \sin \phi }{r}\dfrac{\partial }{\partial \theta } + \dfrac{Cos \phi}{r\sin \theta }\dfrac{\partial }{\partial \phi} \text{, and } \\ \dfrac{\partial }{\partial z} &= \cos \theta \dfrac{\partial }{\partial r} - \dfrac{\sin \theta }{r}\dfrac{\partial }{\partial \theta} + 0\dfrac{\partial}{\partial \phi}, \end{align} \nonumber \]
Next \( \dfrac{\partial }{\partial r}, \dfrac{\partial }{\partial \theta }\text{, and }\dfrac{\partial }{\partial \phi}\) from the chain rule:
\[ \begin{align} \dfrac{\partial }{\partial r} &= \left( \dfrac{\partial x}{\partial r} \right)_{ \theta , \phi}\dfrac{\partial }{\partial x} + \left( \dfrac{\partial y}{\partial r} \right)_{ \theta , \phi}\dfrac{\partial }{\partial y} + \left( \dfrac{\partial z}{\partial r} \right)_{ \theta , \phi}\dfrac{\partial }{\partial z}, \\ \dfrac{\partial }{\partial \theta } &= \left( \dfrac{\partial x}{\partial \theta } \right)_{r, \phi}\dfrac{\partial }{\partial x} + \left( \dfrac{\partial y}{\partial \theta } \right)_{r, \phi}\dfrac{\partial }{\partial y} + \left( \dfrac{\partial z}{\partial \theta } \right)_{r, \phi}\dfrac{\partial }{\partial z}\text{, and } \\ \dfrac{\partial }{\partial \phi } &= \left( \dfrac{\partial x}{\partial \phi} \right)_{r, \theta }\dfrac{\partial }{\partial x} + \left( \dfrac{\partial y}{\partial \phi} \right)_{r, \theta}\dfrac{\partial }{\partial y} + \left( \dfrac{\partial z}{\partial \phi} \right)_{r, \theta}\dfrac{\partial }{\partial z}. \end{align} \nonumber \]
Again evaluation of the the many "coefficients" results in:
\[ \begin{align} \left( \dfrac{\partial x}{\partial r} \right)_{ \theta , \phi} &= \dfrac{x}{\sqrt{x^2 + y^2 + z^2}}, & \left( \dfrac{\partial y}{\partial r} \right)_{ \theta , \phi} &= \dfrac{y}{\sqrt{x^2 + y^2 + z^2}}, & \left( \dfrac{\partial z}{\partial r} \right)_{ \theta , \phi} &= \dfrac{z}{\sqrt{x^2 + y^2 + z^2}} \\ \left( \dfrac{\partial x}{\partial \theta} \right)_{r, \phi} &= \dfrac{x z}{\sqrt{x^2 + y^2}}, & \left( \dfrac{\partial y}{\partial \theta } \right)_{r, \phi} &= \dfrac{y z}{\sqrt{x^2 + y^2}}, & \left( \dfrac{\partial z}{\partial \theta} \right)_{r, \phi} &= -\sqrt{x^2 + y^2} \\ \left( \dfrac{\partial x}{\partial \phi} \right)_{r, \theta} &= -y, & \left( \dfrac{\partial y}{\partial \phi} \right)_{r, \theta} &= x, & \text{ and } \left( \dfrac{\partial z}{\partial \phi} \right)_{r, \theta} = 0 \end{align} \nonumber \]
Upon substitution of these "coefficients":
\[\begin{align} \dfrac{\partial }{\partial r} &= \dfrac{x}{\sqrt{x^2 + y^2 + z^2}}\dfrac{\partial }{\partial x} + \dfrac{y}{\sqrt{x^2 + y^2 + z^2}}\dfrac{\partial }{\partial y} + \dfrac{z}{\sqrt{x^2 + y^2 + z^2}}\dfrac{\partial }{\partial z} \\ \dfrac{\partial }{\partial \theta} &= \dfrac{x z}{\sqrt{x^2 + y^2}}\dfrac{\partial }{\partial x} + \dfrac{y z}{\sqrt{x^2 + y^2}}\dfrac{\partial }{\partial y} - \sqrt{x^2 + y^2}\dfrac{\partial }{\partial z} \\ \dfrac{\partial }{\partial \phi} &= -y\dfrac{\partial }{\partial x} + x\dfrac{\partial }{\partial y} + 0\dfrac{\partial }{\partial z}. \end{align} \nonumber \]
Note, these many "coefficients" are the elements which make up the Jacobian matrix used whenever one wishes to transform a function from one coordinate representation to another. One very familiar result should be in transforming the volume element \(dx\,dy\,dz\) to \(r^2sin \theta \,dr\,d \theta \,d \phi.\) For example:
\[ \int f(x, y, z) dxdydz = \int\limits{ f(x(r, \theta , \phi),y(r, \theta , \phi),z(r, \theta , \phi)) \begin{vmatrix} \left( \dfrac{\partial x}{\partial r} \right)_{\theta \phi} & \left( \dfrac{\partial x}{\partial \theta } \right)_{r \phi} & \left( \dfrac{\partial x}{\partial \phi} \right)_{r \theta} \\ \left( \dfrac{\partial y}{\partial r} \right)_{ \theta \phi} & \left( \dfrac{\partial y}{\partial \theta} \right)_{r \phi} & \left( \dfrac{\partial y}{\partial \phi} \right)_{r \theta} \\ \left( \dfrac{\partial z}{\partial r} \right)_{ \theta \phi} & \left( \dfrac{\partial z}{\partial \theta} \right)_{r \phi} & \left( \dfrac{\partial z}{\partial \phi} \right)_{r \theta } \end{vmatrix} drd \theta d \phi} \nonumber \]
a. \( \begin{align} L_x &= \dfrac{\hbar}{i} \left[ y\dfrac{\partial }{\partial z} - z\dfrac{\partial }{\partial y} \right] \\ L_x &= \dfrac{\hbar}{i} \left[ rsin \theta sin \phi \left( \cos \theta \dfrac{\partial }{\partial r} - \dfrac{\sin \theta }{r}\dfrac{\partial }{\partial \theta } \right) \right] - \dfrac{\hbar}{i} \left[ r\cos \theta \left( \sin \theta \sin \phi\dfrac{\partial }{\partial r} + \dfrac{\cos \theta \sin \phi}{r}\dfrac{\partial }{\partial \theta }+ \dfrac{\cos \phi}{r\sin \theta }\dfrac{\partial }{\partial \phi} \right) \right] \\ L_x &= -\dfrac{\hbar}{i} \left( \sin \phi\dfrac{\partial }{\partial \theta } + \cot \theta \cos \phi\dfrac{\partial }{\partial \phi} \right) \end{align} \)
b. \( \begin{align} L_z &= \dfrac{\hbar}{i}\dfrac{\partial }{\partial \phi} = -i\hbar\dfrac{\partial }{\partial \phi} \\ L_z &= \dfrac{\hbar}{i} \left( -y\dfrac{\partial }{\partial x} + x\dfrac{\partial }{\partial y} \right) \end{align} \)
Q3
\( \begin{align} {}& & B & & B' & & B'' & \\ i. & &4x^4 -12x^2 +3 & & 16x^3 -24x & & 48x^2 - 24 & \\ ii. & & 5x^4 & & 20x^3 & & 60x^2 & \\ iii. & & e^{3x} + e^{-3x} & & 3 \left( e^{3x} - e^{3x} \right) & & 9 \left( e^{3x} + e^{-3x} \right) & \\ iv. & & x^2 - 4x + 2 & & 2x - 4 & & 2 & \\ v. & & 4x^3 -3 & & 12x^2 - 3 & & 24x & \end{align} \)
B(v.) is an eigenfunction of A(i.):
\( \begin{align} &\left( 1 - x^2 \right) \dfrac{d^2}{dx^2} - x\dfrac{d }{dx}\text{B(v.)} &= \\ & &= & \left( 1 - x^2 \right) (24x) - x \left( 12x^2 - 3 \right) \\ & &= & 24x - 24x^3 - 12x^3 + 3x \\ & &= & -36x^3 + 27x \\ & &= & -9 \left( 4x^3 - 3x \right) \text{ (eigenvalue is -9)} \end{align} \)
B(iii.) is an eigenfunction of A(ii.):
\( \begin{align} &\dfrac{d^2 }{dx^2}\text{B(iii.)} &= \\ & &= & 9\left( e^{3x} + e^{-3x} \right) \text{ (eigenvalue is 9)} \end{align} \)
B(ii.) is an eigenfunction of A(iii.):
\( \begin{align} & x\dfrac{d}{dx}\text{B(ii.)} &= \\ & &= & x\left( 20x^3 \right) \\ & &= & 20x^4 \\ & &= & 4 \left( 5x^4 \right) \text{ (eigenvalue is 4)} \end{align} \)
B(i.) is an eigenfunction of A(vi.):
\( \begin{align} &\dfrac{d^2 }{dx^2} - 2x\dfrac{d }{dx}\text{B(i.)} &= \\ & &= & \left( 48x^2 - 24 \right) - 2x \left( 16x^3 - 24x \right) \\ & &= & 48x^2 - 24 -32x^4 + 48x^2 \\ & &= &-32x^4 + 6x^2 - 24 \\ & & =& -8 \left( 4x^4 - 12x^2 + 3 \right) \text{ (eigenvalue is -8)} \end{align} \)
B(iv.) is an eigenfunction of A(v.):
\( \begin{align} &x\dfrac{d^2 }{dx^2} -+(1-x)\dfrac{d }{dx}\text{B(iv.)} &= \\ & &= & x(2) + (1-x)(2x - 4) \\ & &= & 2x + 2x - 4 -2x^2 + 4x \\ & &= &-2x^2 + 8x - 4 \\ & & =& -2 \left( x^2 - 4x + 2 \right) \text{ (eigenvalue is -2)} \end{align} \)
Q4
Show that:
\[ \int f^{\text{*}}\textbf{A}gd\tau = \int g(\textbf{A}f)^{\text{*}}d\tau \nonumber \]
a. Suppose f and g are functions of x and evaluate the integral on the left hand side by "integration by parts":
\[ \int f(x)^{\text{*}} \left( -i\hbar\dfrac{\partial }{\partial x} \right) g(x)dx \nonumber \]
let dv = \( \dfrac{\partial }{\partial x}g(x)dx \) and \( u = -i\hbar f(x)^{\text{*}}\)
\( v = g(x) du = -i\hbar\dfrac{\partial }{\partial x}f(x)^{\text{*}}dx \)
Now, \( \int udv = uv - \int vdu ,\)
so:
\[ f(x)^{\text{*}} \left( -i\hbar\dfrac{\partial }{\partial x} \right)g(x)dx = -i\hbar f(x)^{\text{*}}g(x) + i\hbar\int g(x)\dfrac{\partial }{\partial x}f(x)^{\text{*}}dx. \nonumber \]
Note that in, principle, it is impossible to prove hermiticity unless you are given knowledge of the type of function on which the operator is acting. Hermiticity requires (as can be seen in this example) that the term -i\(\hbar\)f(x)*g(x) vanish when evaluated at the integral limits. This, in general, will occur for the "well behaved" functions (e.g., in bound state quantum chemistry, the wavefunctions will vanish as the distances among particles approaches infinity). So, in proving the hermiticity of an operator, one must be careful to specify the behavior of the functions on which the operator is considered to act. This means that an operator may be hermitian for one class of functions and non-hermitian for another class of functions. If we assume that f and g vanish at the boundaries, then we have
\[ \int f(x)^{\text{*}} \left( -i\hbar \dfrac{\partial }{\partial x}\right) g(x)dx = \int g(x) \left( -\hbar\dfrac{\partial }{\partial x}(x) \right)^{\text{*}} dx \nonumber \]
b. Suppose f and g are functions of y and z and evaluate the integral on the left hand side by "integration by parts" as in the previous exercise:
\[ \int f(y,z)^{\text{*}} \left[ -i\hbar \left( y \dfrac{\partial }{\partial z} - z\dfrac{\partial }{\partial y} \right) \right] g(y,z)dydz = \int f(y,z)^{\text{*}} \left[ -i\hbar \left( y \dfrac{\partial }{\partial z}\right) \right] g(y,z)dydz - \int (y,z)^{\text{*}} \left[ -i\hbar \left( z\dfrac{\partial }{\partial y} \right) \right] g(y,z)dydz \nonumber \]
For the first integral, \( \int f(z)^{\text{*}} \left( -i\hbar y\dfrac{\partial }{\partial z} \right) g(z)dz, \)
\[ \begin{align} \text{let dv } &= \dfrac{\partial }{\partial z}g(z)dz & u &= -i\hbar yf(z)^{\text{*}} \\ v &= g(z) & du &= -i\hbar y\dfrac{\partial }{\partial z}(z)^{\text{*}}dz \end{align} \nonumber \]
so:
\[ \int f(z)^{\text{*}} \left( -i\hbar y\dfrac{\partial }{\partial z} \right) g(z)dz = -i\hbar yf(z)^{\text{*}}g(z) + i\hbar y\int g(z)\dfrac{\partial }{\partial z}f(z)^{\text{*}}dz = \int g(z) \left( -i\hbar y\dfrac{\partial }{\partial z}f(z) \right)^{\text{*}}dz . \nonumber \]
For the second integral, \( \int f(y)^{\text{*}} \left( -i\hbar y\dfrac{\partial }{\partial y} \right) g(y)dy, \)
\[ \begin{align} \text{let dv } &= \dfrac{\partial }{\partial y}g(y)dy & u &= -i\hbar yf(y)^{\text{*}} \\ v &= g(y) & du &= -i\hbar z\dfrac{\partial }{\partial y}f(y)^{\text{*}}dy \end{align}. \nonumber \]
so:
\[ \int f(y)^{\text{*}} \left( -i\hbar z\dfrac{\partial }{\partial y} \right) g(y)dy = -i\hbar zf(y)^{\text{*}}g(y) + i\hbar z\int g(y)\dfrac{\partial }{\partial y}f(y)^{\text{*}}dy = \int g(y) \left( -i\hbar z\dfrac{\partial }{\partial y}f(y) \right)^{\text{*}}dy. \nonumber \]
\[ \int f(y,z)^{\text{*}} \left[ -i\hbar \left( y \dfrac{\partial }{\partial z} - z\dfrac{\partial }{\partial y} \right) \right] g(y,z)dydz = \int g(z) \left( -i\hbar y\dfrac{\partial }{\partial z}f(z) \right)^{\text{*}}dz - \int g(y) \left( -i\hbar z\dfrac{\partial }{\partial y}f(y) \right)^{\text{*}}dy \nonumber \]
\[ = \int g(y,z) \left( -\hbar \left( y\dfrac{\partial }{\partial z} - z\dfrac{\partial }{\partial y} \right) f(y,z) \right)^{\text{*}}dydz. \nonumber \]
Again we have had to assume that the functions f and g vanish at the boundary.
Q5
\[ L_+ = \textbf{L}_x + i\textbf{L}_y \nonumber \]
\[ L_- = \textbf{L}_x - i\textbf{L}_y \text{, so} \nonumber \]
\[ \textbf{L}_+ + \textbf{L}_- = 2\textbf{L}_x, \text{ or } \textbf{L}_x = \dfrac{1}{2}(\textbf{L}_+ + \textbf{L}_-) \nonumber \]
\[ \textbf{L}_+ Y_{l,m} = \sqrt{ l(l + l) - m(m + l)}\hbar T_{l,m+1} \nonumber \]
\[ \textbf{L}_- Y_{l,m} = \sqrt{ l(l + l) - m(m - l)}\hbar T_{l,m-1} \nonumber \]
Using these relationships:
\[ \textbf{L}_- \Psi_{2p_{-1}} = 0 , \textbf{L}_- \Psi_{2p_0} = \sqrt{2}\hbar \Psi_{2p_{-1}}, \textbf{L}_- \Psi_{2p_{+1}} = \sqrt{2}\hbar \Psi_{2p_0} \nonumber \]
\[ \textbf{L}_+ \Psi_{2p_{-1}} = \sqrt{2}\hbar \Psi_{2p_0} , \textbf{L}_+ \Psi_{2p_0} = \sqrt{2}\hbar \Psi_{2p_{+1}} , \textbf{L}_+ \Psi_{2p_{+1}} = 0 \text{ , and the following L}_x \text{ matrix elements can be evaluated: } \nonumber \]
\[ L_x (1,1) = \langle \Psi_{2p_{-1}} \big| \dfrac{1}{2} \left( \textbf{L}_+ + \textbf{L}_- \right) \big| \Psi_{2p_{-1}} \rangle = 0 \nonumber \]
\[ L_x(1,2) = \langle \Psi_{2p_{-1}} \big| \dfrac{1}{2}\left( \textbf{L}_+ + \textbf{L}_- \right) \big| \Psi_{2p_{0}} \rangle = \dfrac{ \sqrt{2}}{2} \hbar \nonumber \]
\[ L_x(1,3) = \langle \Psi_{2p_{-1}} \big| \dfrac{1}{2}\left( \textbf{L}_+ + \textbf{L}_- \right) \big| \Psi_{2p_{+1}} \rangle = 0 \nonumber \]
\[ L_x(2,1) = \langle \Psi_{2p_{0}} \big| \dfrac{1}{2}\left( \textbf{L}_+ + \textbf{L}_- \right) \big| \Psi_{2p_{-1}} \rangle = \dfrac{ \sqrt{2}}{2} \hbar \nonumber \]
\[ L_x(2,2) = \langle \Psi_{2p_{0}} \big| \dfrac{1}{2}\left( \textbf{L}_+ + \textbf{L}_- \right) \big| \Psi_{2p_{0}} \rangle = 0 \nonumber \]
\[ L_x(2,3) = \langle \Psi_{2p_{0}} \big| \dfrac{1}{2}\left( \textbf{L}_+ + \textbf{L}_- \right) big| \Psi_{2p_{+1}} \rangle = \dfrac{ \sqrt{2}}{2} \hbar \nonumber \]
\[ L_x(3,1) = \langle \Psi_{2p_{+1}} \big| \dfrac{1}{2}\left( \textbf{L}_+ + \textbf{L}_- \right) \big| \Psi_{2p_{-1}} \rangle = 0 \nonumber \]
\[ L_x(3,2) = \langle \Psi_{2p_{+1}} \big| \dfrac{1}{2}\left( \textbf{L}_+ + \textbf{L}_- \right) \big| \Psi_{2p_{-1}} \rangle = \dfrac{ \sqrt{2}}{2} \hbar \nonumber \]
\[ L_x(3,3) = 0 \nonumber \]
This matrix: \(\begin{align} \begin{bmatrix} 0 & \dfrac{\sqrt{2}}{2}\hbar & 0 \\ \dfrac{\sqrt{2}}{2}\hbar & 0 & \dfrac{\sqrt{2}}{2}\hbar \\ 0 & \dfrac{ \sqrt{2}}{2} \hbar & 0 \end{bmatrix} \end{align} \), can now be diagonalized:
\[ \begin{align} \begin{vmatrix} 0 - \lambda & \dfrac{\sqrt{2}}{2}\hbar & 0 \\ \dfrac{\sqrt{2}}{2}\hbar & 0 & \dfrac{\sqrt{2}}{2}\hbar \\ 0 & \dfrac{\sqrt{2}}{2} & 0 \end{vmatrix} \end{align} = 0 \nonumber \]
\( \begin{align} \begin{vmatrix} 0 - \lambda & \dfrac{\sqrt{2}}{2}\hbar \\ \dfrac{\sqrt{2}}{2}\hbar & 0 -\lambda \end{vmatrix} \end{align} ( -\lambda )\) -\( \begin{align} \begin{vmatrix} \dfrac{\sqrt{2}}{2}\hbar & \dfrac{\sqrt{2}}{2}\hbar \\ 0 & 0 - \lambda \end{vmatrix} \end{align} \left( \dfrac{\sqrt{2}}{2}\hbar \right) = 0 \)
Expanding theses determinants yields:
\[ \left( \lambda^2 - \dfrac{\hbar^2}{2} \right) (-\lambda ) - \dfrac{\sqrt{2}\hbar}{2}( -\lambda ) \left( \dfrac{\sqrt{2}\hbar}{2} \right) = 0 \nonumber \]
\[ -\lambda \left( \lambda^2 - \hbar^2 \right) = 0 \nonumber \]
\[ -\lambda \left( \lambda - \hbar \right) \left( \lambda + \hbar \right) = 0 \nonumber \]
with roots: 0,\(\hbar \text{, and } -\hbar \)
Next, determine the corresponding eigenvectors:
For \(\lambda = 0\)
\[ \begin{align} \begin{bmatrix} 0 & \dfrac{\sqrt{2}}{2}\hbar & 0 \\ \dfrac{\sqrt{2}}{2}\hbar & 0 & \dfrac{\sqrt{2}}{2}\hbar \\ 0 & \dfrac{\sqrt{2}}{2}\hbar & 0 \end{bmatrix} \end{align} \begin{bmatrix} C_{11} \\ C_{21} \\ C_{31} \end{bmatrix} = 0 \begin{bmatrix} C_{11} \\ C_{21} \\ C_{31} \end{bmatrix} \nonumber \]
\[ \dfrac{\sqrt{2}}{2}\hbar C_{21} = 0 \text{ (row one) } \nonumber \]
\[ C_21 = 0 \nonumber \]
\[ \dfrac{\sqrt{2}}{2}\hbar C_{11} + \dfrac{\sqrt{2}}{2}\hbar C_{31} = 0 \text { (row two)} \nonumber \]
\[ C_{11} + C_{31} = 0 \nonumber \]
\[ C_{11} = -C_{31} \nonumber \]
\[ C_{11}^2 + C_{21}^2 + C_{31}^2 = 1 \text{ (normalization)} \nonumber \]
\[ C_{11}^2 + (-C_{11})^2 = 1 \nonumber \]
\[ 2C_{11}^2 = 1 \nonumber \]
\[ C_{11} = \dfrac{1}{\sqrt{2}}, C_{21} = 0\text{, and } C_{31} = -\dfrac{1}{\sqrt{2}} \nonumber \]
For \(\lambda = 1\hbar : \)
\[ \begin{align} \begin{bmatrix} 0 & \dfrac{\sqrt{2}}{2}\hbar & 0 \\ \dfrac{\sqrt{2}}{2}\hbar & 0 & \dfrac{\sqrt{2}}{2}\hbar \\ 0 & \dfrac{\sqrt{2}}{2}\hbar & 0 \end{bmatrix} \end{align} \begin{bmatrix} C_{12} \\ C_{22} \\ C_{32} \end{bmatrix} = 0 \begin{bmatrix} C_{12} \\ C_{22} \\ C_{32} \end{bmatrix} \nonumber \]
\[ \dfrac{\sqrt{2}}{2}\hbar C_{22} = \hbar C_{12} \text{ (row one)} \nonumber \]
\[ C_{12} = \dfrac{\sqrt{2}}{2}C_{22} \nonumber \]
\[ \dfrac{\sqrt{2}}{2}\hbar C_{12} + \dfrac{\sqrt{2}}{2}\hbar C_{32} = \hbar C_{22} \text{ (row two)} \nonumber \]
\[ \dfrac{\sqrt{2}}{2}\dfrac{\sqrt{2}}{2} C_{22} + \dfrac{\sqrt{2}}{2} C_{32} = C_{22} \nonumber \]
\[ \dfrac{1}{2} C_{22} + \dfrac{\sqrt{2}}{2} C_{32} = C_{22} \nonumber \]
\[ \dfrac{\sqrt{2}}{2} C_{32} = \dfrac{1}{2} C_{22} \nonumber \]
\[ C_{32} = \dfrac{\sqrt{2}}{2} C_{22} \nonumber \]
\[ C_{12}^2 + C_{22}^2 + C_{32}^2 = 1\text{ (normalization)} \nonumber \]
\[ \left( \dfrac{\sqrt{2}}{2}C_{22} \right)^2 + C_{22}^2 + \left( \dfrac{\sqrt{2}}{2}C_{22}\right)^2 = 1 \nonumber \]
\[ \dfrac{1}{2}C_{22}^2 + C_{22}^2 + \dfrac{1}{2}C_{22}^2 = 1 \nonumber \]
\[ 2C_{22}^2 = 1 \nonumber \]
\[ C_{22} = \dfrac{\sqrt{2}}{2} \nonumber \]
\[ C_{12} = \dfrac{1}{2}, C_{22} = \dfrac{\sqrt{2}}{2}\text{, and } C_{32} = \dfrac{1}{2} \nonumber \]
For \( \lambda = -1 \hbar \)
\[ \begin{align} \begin{bmatrix} 0 & \dfrac{\sqrt{2}}{2}\hbar & 0 \\ \dfrac{\sqrt{2}}{2}\hbar & 0 & \dfrac{\sqrt{2}}{2}\hbar \\ 0 & \dfrac{\sqrt{2}}{2}\hbar & 0 \end{bmatrix} \end{align} \begin{bmatrix} C_{13} \\ C_{23} \\ C_{33} \end{bmatrix} = 0 \begin{bmatrix} C_{13} \\ C_{23} \\ C_{33} \end{bmatrix} \nonumber \]
\[ \dfrac{\sqrt{2}}{2}\hbar C_{23} = - \hbar C_{13} \text{ (row one) } \nonumber \]
\[ C_{13} = - \dfrac{\sqrt{2}}{2} C_{23} \nonumber \]
\[ \dfrac{\sqrt{2}}{2}\hbar C_{13} + \dfrac{\sqrt{2}}{2}\hbar C_{33} = -\hbar C_{23} \text{ (row two)} \nonumber \]
\[ \dfrac{\sqrt{2}}{2} \left( -\dfrac{\sqrt{2}}{2} C_{23} \right) + \dfrac{\sqrt{2}}{2} C_{33} = -C_{23} \nonumber \]
\[ -\dfrac{1}{2} C_{23} + \dfrac{\sqrt{2}}{2} C_{33} = -C_{23} \nonumber \]
\[ \dfrac{\sqrt{2}}{2} C_{33} = -\dfrac{1}{2} C_{23} \nonumber \]
\[ C_{33} = -\dfrac{\sqrt{2}}{2} C_{23} \nonumber \]
\[ C_{13}^2 + C_{23}^2 + C_{33}^2 = 1 \text{ (normalization)} \nonumber \]
\[ \left( -\dfrac{\sqrt{2}}{2} C_{23} \right)^2 + C_{23}^2 + \left( -\dfrac{\sqrt{2}}{2}C_{23} \right)^2 = 1 \nonumber \]
\[ \dfrac{1}{2}C_{23}^2 + C_{23}^2 + \dfrac{1}{2}C_{23}^2 = 1 \nonumber \]
\[ 2C_{23}^2 = 1 \nonumber \]
\[ C_{23} = \dfrac{\sqrt{2}}{2} \nonumber \]
\[ C_{13} = -\dfrac{1} , C_{23} = \dfrac{\sqrt{2}}{2} \text{, and } C_{33} = -\dfrac{1}{2} \nonumber \]
Show: \( \langle \phi_1 | \phi_1 \rangle = 1, \langle \phi_2 | \phi_2 \rangle = 1, \langle \phi_3 | \phi_3 \rangle = 1, \langle \phi_1 | \phi_2 \rangle = 0, \langle \phi_1 | \phi_3 \rangle = 0 \text{, and} \langle \phi_2 | \phi_3 \rangle = 0. \)
\[ \langle \phi_1 | \phi_1 \rangle \stackrel{?}{=} 1 \nonumber \]
\[ \left( \dfrac{\sqrt{2}}{2} \right)^2 + 0 + \left( -\dfrac{\sqrt{2}}{2} \right)^2 \stackrel{?}{=} 1 \nonumber \]
\[ \dfrac{1}{2} + \dfrac{1}{2} \stackrel{?}{=} 1 \nonumber \]
\[ 1 = 1 \nonumber \]
\[ \langle \phi_2 | \phi_2 \rangle \stackrel{?}{=} 1 \nonumber \]
\[ \left( \dfrac{1}{2} \right)^2 + \left( \dfrac{\sqrt{2}}{2} \right)^2 + \left( \dfrac{1}{2} \right)^2 \stackrel{?}{=} 1 \nonumber \]
\[ \dfrac{1}{4} + \dfrac{1}{2} + \dfrac{1}{4} \stackrel{?}{=} 1 \nonumber \]
\[ 1 = 1 \nonumber \]
\[ \langle \phi_3 | \phi_3 \rangle \stackrel{?}{=} 1 \nonumber \]
\[ \left( -\dfrac{1}{2}\right)^2 + \left( \dfrac{\sqrt{2}}{2} \right)^2 + \left(-\dfrac{1}{2}\right)^2 \stackrel{?}{=} 1 \nonumber \]
\[ \dfrac{1}{4} + \dfrac{1}{2} + \dfrac{1}{4} \stackrel{?}{=} 1 \nonumber \]
\[ 1 = 1 \nonumber \]
\[ \langle \phi_1 | \phi_2 \rangle = \langle \phi_2 | \phi_1 \rangle \stackrel{?}{=} 0 \nonumber \]
\[ \left( \dfrac{\sqrt{2}}{2} \right) \left( \dfrac{1}{2} \right) + (0)\left( \dfrac{\sqrt{2}}{2} \right) + \left( -\dfrac{\sqrt{2}}{2} \right)\left( \dfrac{1}{2} \right) \stackrel{?}{=} 0 \nonumber \]
\[ \left( \dfrac{\sqrt{2}}{4} \right) - \left( \dfrac{\sqrt{2}}{4} \right) \stackrel{?}{=} 0 \nonumber \]
\[ 0 = 0 \nonumber \]
\[ \langle \phi_1 | \phi_3 \rangle = \langle \phi_3 | \phi_1 \rangle \stackrel{?}{=} 0 \nonumber \]
\[ \left( \dfrac{\sqrt{2}}{2} \right) \left( -\dfrac{1}{2} \right) + (0)\left( \dfrac{\sqrt{2}}{2} \right) + \left( -\dfrac{\sqrt{2}}{2} \right)\left( -\dfrac{1}{2} \right) \stackrel{?}{=} 0 \nonumber \]
\[ \left( -\dfrac{\sqrt{2}}{4} \right) + \left( \dfrac{\sqrt{2}}{4}\right) \stackrel{?}{=} 0 \nonumber \]
\[ 0 = 0 \nonumber \]
\[ \langle \phi_2 | \phi_3 \rangle = \langle \phi_3 | \phi_2 \rangle \stackrel{?}{=} 0 \nonumber \]
\[ \left( \dfrac{1}{2}\right) \left( -\dfrac{1}{2}\right) + \left( \dfrac{\sqrt{2}}{2} \right) \left( \dfrac{\sqrt{2}}{2} \right) + \left( \dfrac{1}{2} \right) \left( -\dfrac{1}{2} \right) \stackrel{?}{=} 0 \nonumber \]
\[ \left(-\dfrac{1}{4}\right) + \left(\dfrac{1}{2}\right) + \left(-\dfrac{1}{4}\right) \stackrel{?}{=} 0 \nonumber \]
\[ 0 = 0 \nonumber \]
Q6
\[ P_{2p_{+1}} = \big| \langle \phi_{2p_{+1}} \Phi_{L_x}^{0\hbar} \rangle \big|^2 \nonumber \]
\[ \Psi_{L_x}^{0\hbar} = \dfrac{1}{\sqrt{2}} \phi_{2p_{-1}} - \dfrac{1}{\sqrt{2}}\phi_{2p_{+1}} \nonumber \]
\[ P_{2p_{+1}} = \big| -\dfrac{1}{\sqrt{2}} \langle \phi_{20_{+1}} \phi_{2p_{+1}} \rangle \big|^2 = \dfrac{1}{2} \text{ (or 50%)} \nonumber \]
Q7
It is useful here to use some of the general commutator relations found in Appendix C.V.
a. \[ \left[ L_x,L_y \right] = \left[ yp_z - zp_y, zp_x - xp_z \right] \nonumber \]
\[ = \left[ yp_z, zp_x \right] - \left[ yp_z, xp_z \right] - \left[ zp_y, zp_x \right] + \left[ zp_y, xp_z \right] \nonumber \]
\[ = [y,z]p_xp_z + z[y,p_x]p_z + y[p_z,z]p_x + yz[p_z,p_x] \nonumber \]
\[ - [y,x]p_zp_z - x[y,p_z]p_z - y[p_z,x]p_z - yx[p_z,p_z] \nonumber \]
\[ - [z,z]p_xp_y - z[z,p_x]p_y - z[p_y,z]p_x - zz[p_y,p_x] \nonumber \]
\[ + [z,x]p_zp_y + x[z,p_z]p_y + z[p_y.x]p_z + zx[p_y,p_z] \nonumber \]
As can be easily ascertained, the only non-zero terms are:
\[ \left[ L_x, L_y \right] = y\left[ p_z,Z \right] p_x + x\left[ z,p_z \right] p_y \nonumber \]
\[ = y( i\hbar )p_x + x( i\hbar )p_y \nonumber \]
\[ = i\hbar \left( -yp_x + xp_y \right) \nonumber \]
\[ = i\hbar L_z \nonumber \]
b. \[ \left[ L_y,L_z \right] = \left[ zp_x - xp_z, xp_y - yp_z \right] \nonumber \]
\[ = \left[ zp_x, xp_y \right] - \left[ zp_x, yp_x \right] - \left[ xp_z, xp_y \right] + \left[ xp_z, yp_x \right] \nonumber \]
\[ = [z,x]p_yp_x + x\left[ z, p_y\right]p_x + z\left[ p_x,x\right] p_y + zx\left[ p_x,p_z \right] \nonumber \]
\[ - [z,y]P_xp_x - y\left[z,p_x\right] p_x - z\left[ p_x,y \right] p_x - zy\left[ p_x, p_x \right] \nonumber \]
\[ - [x,x]p_yp_z - x\left[x,p_y\right] p_z - x\left[ p_z,x \right] p_y - xx\left[ p_z, p_y \right] \nonumber \]
\[ +[x,y]p_xp_z + y\left[ x,p_x \right] p_z + x\left[ p_z, y\right] p_x + xy\left[ p_z ,p_x \right] \nonumber \]
Again, as can be easily ascertained, the only non-zero terms are:
\[ \left[ L_y, L_z \right] = z \left[ p_x,x \right] p_y + y\left[ x,p_x \right] p_z \nonumber \]
\[ = z( -i\hbar )p_y + y(i\hbar )p_z \nonumber \]
\[ = i\hbar (-zp_y + yp_z) \nonumber \]
\[ =i\hbar L_x \nonumber \]
c. \[ \left[ L_z, L_x \right] = \left[ xp_y - yp_x, yp_z - zp_y \right] \nonumber \]
\[ = \left[ xp_y, yp_z \right] - \left[ xp_y, zp_y \right] - \left[ yp_x, yp_z \right] + \left[ yp_x, zp_y \right] \nonumber \]
\[ = \left[ x,y \right] p_zp_y + y\left[ x,p_z \right] p_y + x\left[ p_y, y \right] p_z + xy\left[ p_y, p_z \right] \nonumber \]
\[ - \left[ x,z \right] p_yp_y - z\left[ x,p_y \right] p_y - x\left[ p_y, z \right] p_y - xz\left[ p_y, p_y \right] \nonumber \]
\[ - \left[ y, y \right] p_zp_x - z\left[ y,p_y \right] p_x - y\left[ p_x, y \right] p_z - yy\left[ p_x, p_z \right] \nonumber \]
\[ + \left[ y, z \right] p_yp_x + z\left[ y,p_y \right] p_x + y\left[ p_x, z \right] p_y + yz\left[ p_x, p_z \right] \nonumber \]
Again, as can be easily ascertained, the only non-zero terms are:
\[ \left[ L_z, L_x \right] = x\left[ p_y, y\right] p_z + z\left[ y,p_y \right] p_x \nonumber \]
\[ = x(-i\hbar)p_z + z(i\hbar )p_x \nonumber \]
\[ = i\hbar (-xp_z + zp_x) \nonumber \]
\[ = i\hbar L_y \nonumber \]
d. \[ \left[ L_x, L^2 \right] = \left[ L_x. L_x^2 + L_y^2 + L_z^2 \right] \nonumber \]
\[ = \left[ L_x, L_x^2 \right] + \left[ L_x, L_y^2 \right] + \left[ L_x, L_z^2 \right] \nonumber \]
\[ = \left[ L_x, L_y^2 \right] + \left[ L_x, L_z^2 \right] \nonumber \]
\[ = \left[ L_x, L_y \right] L_y + L_y\left[ L_x. L_y \right] + \left[ L_x, L_z \right] L_z + L_z\left[ L_x, L_z \right] \nonumber \]
\[ = \left( i\hbar L_z \right) L_y + L_y\left( i\hbar L_z \right) + \left( -i\hbar L_y \right) L_z + L_z\left( -i\hbar L_y \right) \nonumber \]
\[ = (i\hbar )\left( -L_zL_x - L_xL_z + L_xL_z + L_zL_x \right) \nonumber \]
\[ = (i\hbar )\left( \left[ L_z, L_y \right] + \left[ L_y, L_z \right] \right) = 0 \nonumber \]
e. \[ \left[ L_y, L^2 \right] = \left[ L_y, L_x^2 + L_y^2 + L_z^2 \right] \nonumber \]
\[ = \left[ L_y, L_x^2 \right] + \left[ L_y, L_y^2 \right] + \left[ L_y, L_z^2 \right] \nonumber \]
\[ = \left[ L_z, L_x^2 \right] + \left[ L_z, L_y^2 \right] \nonumber \]
\[ = \left[ L_y, L_x \right] L_x + L_x\left[ L_y, L_x \right] + \left[ L_y, L_z \right] L_z + L_z\left[ L_y, L_z \right] \nonumber \]
\[ = \left( -i \hbar L_z \right) L_x + L_x \left( -i\hbar L_z \right) + \left( i\hbar L_x \right) L_z + L_z \left( i\hbar L_x\right) \nonumber \]
\[ = \left( i\hbar \right) \left( -L_z L_x - L_x L_z + L_x L_z + L_z L_x \right) \nonumber \]
\[ = \left( i\hbar \right) \left( \left[ L_x, L_z \right] + \left[ L_z, L_x \right] \right) = 0 \nonumber \]
f. \[ \left[ L_z, L^2 \right] = \left[ L_z, L_x^2 + L_y^2 + L_z^2 \right] \nonumber \]
\[ = \left[ L_z, L_x^2 \right] + \left[ L_z, L_y^2 \right] + \left[ L_z, L_z^2 \right] \nonumber \]
\[ = \left[ L_z, L_x^2 \right] + \left[ L_z, L_y^2 \right] \nonumber \]
\[ = \left[ L_z, L_x \right] L_x + L_x\left[ L_z, L_x \right] + \left[ L_z, L_y \right] L_y + L_y \left[ L_z, L_y \right] \nonumber \]
\[ =\left( i\hbar L_y \right) L_x + L_x \left( i\hbar L_y \right) + \left( -i\hbar L_x\right) L_y + L_y \left( -i\hbar L_x \right) \nonumber \]
\[ \left( i\hbar\right) \left( L_yL_x + L_xL_y - L_xL_y - L_yL_x \right) \nonumber \]
\[ \left( i\hbar\right) \left( \left[ L_y, L_x \right] + \left[ L_x, L_y \right] \right) = 0 \nonumber \]
Q8
Use the general angular momentum relationships:
\[ J^2 \big| j,m \rangle = \hbar^2 \left( j \left( j+1 \right)\right) \big| j,m \rangle \nonumber \]
\[ J_z \big| j,m \rangle = \hbar m \big| j,m \rangle , \nonumber \]
and the information used in exercise 5, namely that:
\[ \textbf{L}_x = \dfrac{1}{2}\left( \textbf{L}_+ + \textbf{L}_- \right) \nonumber \]
\[ \textbf{L}_+ Y_{l,m} = \sqrt{l(l + l) - m(m + l)}\hbar Y_{l,m+1} \nonumber \]
[ \textbf{L}_- Y_{l,m} = \sqrt{l(l + l) - m(m - l)}\hbar Y_{l,m-1} \nonumber \]
Given that:
\[ Y_{0,0} (\theta, \phi) = \dfrac{1}{\sqrt{4\pi}} = \big| 0,0\rangle \nonumber \]
\[ Y_{1,0} (\theta ,\phi ) = \sqrt{\dfrac{3}{4\pi}} Cos\theta = \big| 1,0 \rangle . \nonumber \]
a. \[ \textbf{L}_z \big| 0,0\rangle = 0 \nonumber \]
[ \textbf{L}^2 \big| 0,0\rangle = 0 \nonumber \]
Since \(L^2\) and \(L_z\) commute you would expect |0,0> to be simultaneous eigenfunctions of both.
b. \[ \textbf{L}_x \big| 0,0\rangle = 0 \nonumber \]
\[ \textbf{L}_z \big| 0,0\rangle = 0 \nonumber \]
\(L_x\) and \(L_z\) do not commute. It is unexpected to find a simultaneous eigenfunction (|0,0>) of both ... for sure these operators do not have the same full set of eigenfunctions.
c. \[ \textbf{L}_z \big| 1,0\rangle = 0 \nonumber \]
\[ \textbf{L}^2 \big| 1,0\rangle = 2 \hbar^2 \big| 1,0 \rangle \nonumber \]
Again since \(L^2\) and \(L_z\) commute you would expect |1,0> to be simultaneous eigenfunctions of both.
d. \[ \textbf{L}_x \big| 1,0\rangle = \dfrac{\sqrt{2}}{2} \hbar \big| 1,-1 \rangle + \dfrac{\sqrt{2}}{2} \hbar \big| 1, 1 \rangle \nonumber \]
\[ \textbf{L}_z \big| 1, 0\rangle = 0 \nonumber \]
Again, \(L_x\) and \(L_z\) do not commute. Therefore it is expected to find differing sets of eigenfunctions for both.
Q9
For
\[ \Psi (x,y) = \sqrt{\left( \dfrac{1}{2L_x} \right) \left( \dfrac{1}{2L_y} \right)} \left[ e^{\left( \dfrac{in_x\pi x}{L_x} \right)} - e^{\left( \dfrac{-in_x\pi x}{L_x} \right)} \right] \left[ e^{\left( \dfrac{in_y\pi y}{L_y} \right)} - e^{\left( \dfrac{-in_y\pi y}{L_y} \right)} \right] \nonumber \]
\[ \langle \Psi (x,y) \big| \Psi (x,y) \rangle \stackrel{?}{=} 1 \nonumber \]
Let: \(a_x = \dfrac{n_x\pi}{L_x}\), and \( a_y = \dfrac{n_y\pi}{L_y}\) and using Euler's formula, expand the exponentials into Sin and Cos terms.
\[ \Psi (x,y) = \sqrt{ \left( \dfrac{1}{2L_x} \right) \left( \dfrac{1}{2L_y} \right) } \left[ \cos (a_xx) + i\sin (a_x x) - \cos (a_x x) + i\sin (a_x x) \right] \left[ \cos (a_y y) + i\sin (a_y y) - \cos (a_y y) + i\sin (a_y y) \right] \nonumber \]
\[ \Psi (x,y) = \sqrt{ \left( \dfrac{1}{2L_x} \right) \left( \dfrac{1}{2L_y} \right) } 2i\sin (a_x x) 2i\sin (a_y y) \nonumber \]
\[ \Psi (x,y) = \sqrt{ \left( -\dfrac{2}{L_x} \right) \left( \dfrac{2}{L_y} \right) } \sin (a_x x) \sin (a_y y) \nonumber \]
\[ \langle \Psi (x,y) \big| \Psi (x,y) \rangle = \int \left( \sqrt{ \left( -\dfrac{2}{L_x} \right) \left( \dfrac{2}{L_y} \right) } \sin (a_x x) \sin (a_y y) \right)^2 dxdy \nonumber \]
\[ = \left( \dfrac{2}{L_x} \right) \left( \dfrac{2}{L_y} \right) \int \sin^2 (a_x x) \sin^2 (a_y y) dxdy \nonumber \]
Using the integral:
\[ \int\limits^L_0 \sin^2 \dfrac{n\pi x}{L} dx = \dfrac{L}{2}, \nonumber \]
\[ \angle \Psi (x,y) \big| \Psi (x,y) \rangle = \left( \dfrac{2}{L_x} \right) \left( \dfrac{2}{L_y} \right) \left( \dfrac{L_x}{2} \right) \left( \dfrac{L_y}{2} \right) = 1 \nonumber \]
Q10
\[ \langle \Psi (x,y) | p_x | \Psi (x,y) \rangle = \left( \dfrac{2}{L_y} \right) \int\limits_0^{L_y} \sin^2 (a_y y)dy \left( \dfrac{2}{L_x} \right) \int\limits_0^{L_x} \sin (a_x x)\left( -i\hbar \dfrac{\partial}{\partial x}\right) \sin (a_x x) dx = \left( \dfrac{-i\hbar 2a_x}{L_x} \right) \int\limits_0^{L_x} \sin (a_x x)\cos (a_x x) dx \nonumber \]
But the integral:
\[ \int\limits_0^{L_x} \cos (a_x x)\sin (a_x x) dx = 0, \nonumber \]
\[ \therefore \langle \Psi (x,y) \big| p_x \big| \Psi (x,y) \rangle = 0 \nonumber \]
Q11
\[ \langle \Psi_0 \big| x^2 \big| \Psi_0 \rangle = \sqrt{\dfrac{\alpha}{\pi}}\int\limits_{-\infty}^{\infty}\left( e^{-\dfrac{1}{2}\alpha x^2} \right) \left( \textbf{x}^2 \right) \left( e^{-\dfrac{1}{2}\alpha x^2} \right) dx = 2\sqrt{\dfrac{\alpha}{\pi}}\int\limits_0^{\infty}x^2 e^{-\dfrac{1}{2}\alpha x^2}dx \nonumber \]
Using the integral:
\[ \int\limits_0^{\infty}x^{2n} e^{-\beta x^2}dx = \dfrac{1\cdot{3}\cdot{\cdot{\cdot{(2n-1)}}}}{2^{n+1}}\sqrt{ \left( \dfrac{\pi}{\beta ^{2n + 1}} \right) } \nonumber \]
\[ \langle \Psi_0 | \textbf{x}^2 | \Psi_0 \rangle = 2\sqrt{\dfrac{\alpha}{\pi}} \left( \dfrac{1}{2^2} \right) \sqrt{\dfrac{\pi}{\alpha^3}} \nonumber \]
\[ \langle \Psi_0 | \textbf{x}^2 | \Psi_0 \rangle = \left( \dfrac{1}{2\alpha} \right) \nonumber \]
\[ \langle \Psi_1 | \textbf{x}^2 | \Psi_1 \rangle = \sqrt{\dfrac{4\alpha^3}{\pi}}\int^{\infty}_{-\infty}\left( xe^{-\dfrac{1}{2}\alpha x^2} \right) \left( \textbf{x}^2 \right) \left( xe^{-\alpha \dfrac{1}{2}x^2} \right) dx \nonumber \]
\[ = 2\sqrt{\dfrac{4\alpha^3}{\pi}}\int\limits_0^{\infty} x^4 e^{-\alpha\dfrac{1}{2}x^2}dx \nonumber \]
Using the previously defined integral:
\[ \langle \Psi_1 | \textbf{x}^2 | \Psi_1 \rangle = 2\sqrt{\dfrac{4\alpha^3}{\pi}}\left( \dfrac{3}{2^3} \right) \sqrt{\dfrac{\pi}{\alpha^5}} \nonumber \]
\[ \langle \Psi_1 | \textbf{x}^2 | \Psi_1 \rangle = \left( \dfrac{3}{2\alpha} \right) \nonumber \]
Q12
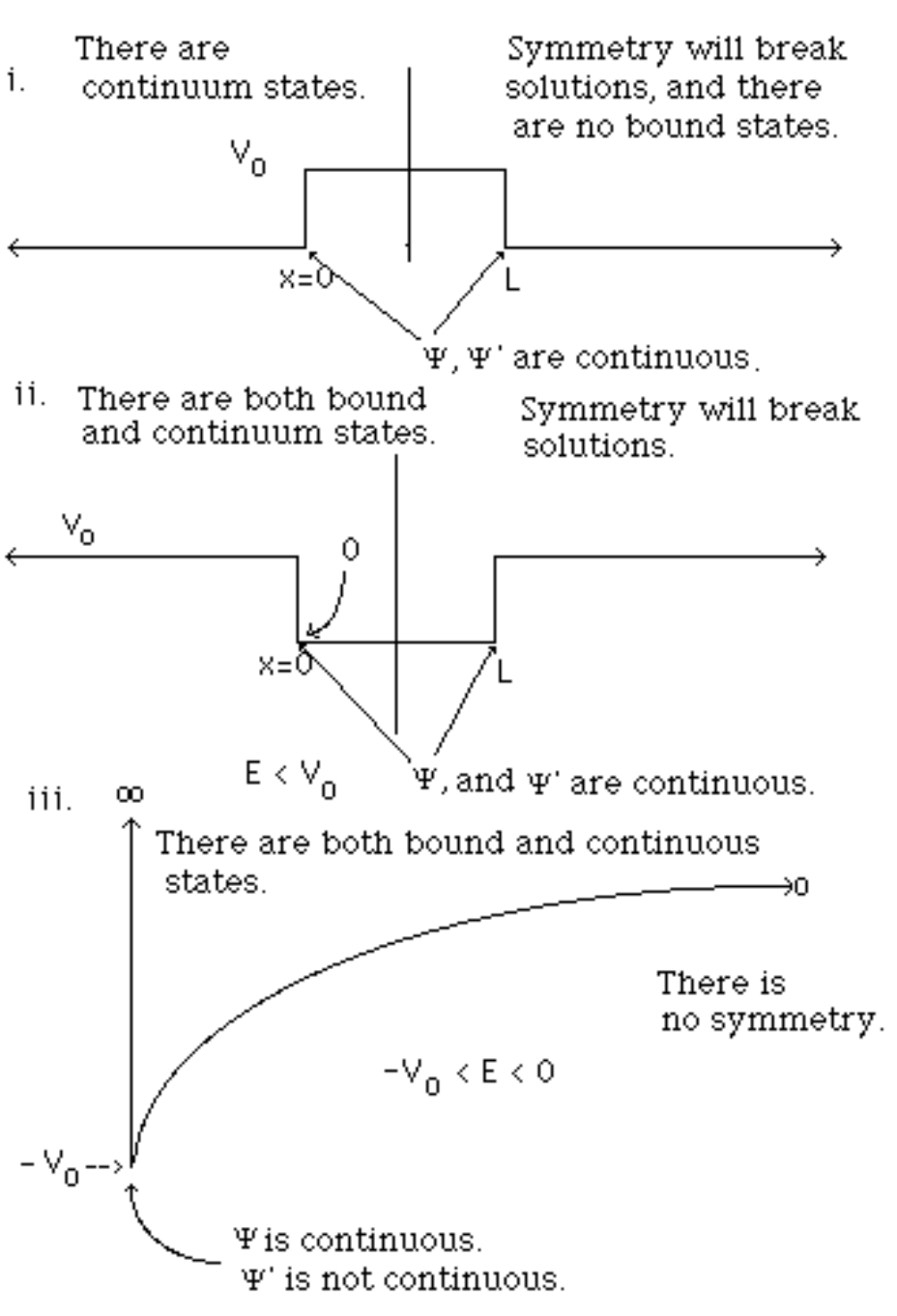
Q13
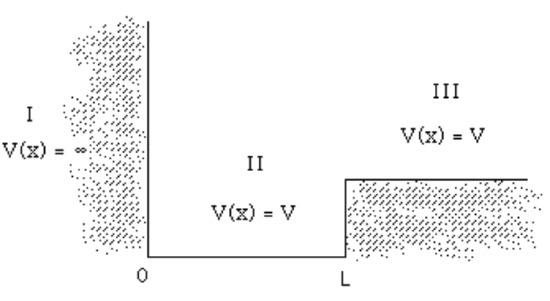
a. \[ \Psi_I (x) = 0 \nonumber \]
\[ \Psi_{II} (x) = Ae^{\left( i\sqrt{\dfrac{2mE}{\hbar^2}}x \right)} + Be^{\left( -i\sqrt{\dfrac{2mE}{\hbar^2}}x \right)} \nonumber \]
\[ \Psi_{III} (x) = A'e^{\left( i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}x \right)} + B'e^{\left( -i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}x \right)} \nonumber \]
b. \[ I \leftrightarrow II \nonumber \]
\[ \Psi_I(0) = \Psi_{II}(0) \nonumber \]
\[ \Psi_I (0) = 0 = \Psi_{II} (0) = Ae^{\left( i\sqrt{\dfrac{2mE}{\hbar^2}}(0) \right)} + Be^{\left( -i\sqrt{\dfrac{2mE}{\hbar^2}}(0) \right)} \nonumber \]
\[ 0 = A + B \nonumber \]
\[ B = -A \nonumber \]
\[ \Psi_I '(0) = \Psi_{II} '(0) \nonumber \]
( this gives no useful information since \(\Psi_I '(x)\) does not exist at x = 0 )
\[ I \leftrightarrow II \nonumber \]
\[ \Psi_{II} (L) = \Psi_{III} (L) \nonumber \]
\[ Ae^{\left( i\sqrt{\dfrac{2mE}{\hbar^2}}L \right)} + Be^{\left( -i\sqrt{\dfrac{2mE}{\hbar^2}}L \right)} = A'e^{\left( i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L \right)} + B'e^{\left( -i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L \right)} \nonumber \]
\[ \Psi_{II}'(L) = \Psi_{III}'(L) A\left( e^{i\sqrt{\dfrac{2mE}{\hbar^2}}L} \right) + B\left( e^{-i\sqrt{\dfrac{2mE}{\hbar^2}}L} \right) = A' \left( e^{i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L} \right) + B' \left( e^{-i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L} \right) \nonumber \]
\[ \Psi_{II}'(L) = \Psi_{III}'(L) \nonumber \]
\[ A \left( i\sqrt{ \dfrac{2mE}{\hbar^2}} \right) e^{i\sqrt{\dfrac{2mE}{\hbar}}L} - B \left( i\sqrt{ \dfrac{2mE}{\hbar^2}} \right) e^{i\sqrt{\dfrac{2mE}{\hbar}}L} \nonumber \]
\[ = A' \left( i\sqrt{ \dfrac{2m(V-E)}{\hbar^2}} \right) e^{i\sqrt{\dfrac{2m(V-E)}{\hbar}}L} - B' \left( i\sqrt{ \dfrac{2m(V-E)}{\hbar^2}} \right) e^{i\sqrt{\dfrac{2m(V-E)}{\hbar}}L} \nonumber \]
c. \[ as x \rightarrow -\infty , \Psi_I (x) = 0 \nonumber \]
\[ as x \rightarrow \infty , \Psi_{III}(x) = 0 \therefore A' = 0 \nonumber \]
d. Rewrite the equations for \(\Psi_I(0), \Psi_{II}(0), \Psi_{II}(L) = \Psi_{III}(L) \text{, and } \Psi_{II}'(L) = \Psi_{III}'(L)\) using the information in 13c:
\[ B = -A (eqn. 1) \nonumber \]
\[ A e^{i\sqrt{\dfrac{2mE}{\hbar}}L} + B e^{-i\sqrt{\dfrac{2mE}{\hbar}}L} = B'e^{i\sqrt{\dfrac{2m(V-E)}{\hbar}}L} \nonumber \]
(eqn. 2)
\[ A\left( i \sqrt{\dfrac{2mE}{\hbar^2}}\right) e^{i\sqrt{\dfrac{2mE}{\hbar}}L} - B\left( i\sqrt{\dfrac{2mE}{\hbar^2}L} \right) e^{-i\sqrt{\dfrac{2mE}{\hbar^2}}L} = -B' \left( i\sqrt{\dfrac{2m(V-E)}{\hbar^2}} \right) e^{ -i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L} \nonumber \]
substitution (eqn. 1) into (eqn. 2)
\[ Ae^{i\sqrt{\dfrac{2mE}{\hbar^2}}L} - Ae^{-i\sqrt{\dfrac{2mE}{\hbar^2}}L} = B'e^{-i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L} \nonumber \]
\[ A \left[ \cos \left( \sqrt{\dfrac{2mE}{\hbar^2}}L \right) + i\sin\left( \sqrt{\dfrac{2mE}{\hbar^2}L} \right) \right] - A \left[ \cos \left( \sqrt{\dfrac{2mE}{\hbar^2}}L \right) - i\sin\left( \sqrt{\dfrac{2mE}{\hbar^2}L} \right) \right] = B'e^{-i\sqrt{\dfrac{(V-E)}{\hbar^2}}L} \nonumber \]
\[ 2Ai\sin \left( \sqrt{\dfrac{2mE}{\hbar^2}}L \right) = B'e^{-i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L} \nonumber \]
\[ \sin \left( \sqrt{\dfrac{2mE}{\hbar^2}}L \right) = \dfrac{B'}{2Ai}e^{-i\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L} \text{ (eqn. 4)} \nonumber \]
substituting (eqn. 1) into (eqn. 3):
\[ A\left( i\sqrt{\dfrac{2mE}{\hbar^2}} \right)e^{\left( i\sqrt{\dfrac{2mE}{\hbar^2}}L \right)} + A\left( i\sqrt{\dfrac{2mE}{\hbar^2}} \right)e^{\left( -i\sqrt{\dfrac{2mE}{\hbar^2}}L \right)} = - B' \left( i\sqrt{\dfrac{2m(V-E)}{\hbar^2}} \right)e^{\left( -1\sqrt{\dfrac{2m(V-E)}{\hbar^2}}L \right) } \nonumber \]
\[ A\left( i\sqrt{\dfrac{2mE}{\hbar^2}} \right) \left( \cos \left( \sqrt{\dfrac{2mE}{\hbar^2}}L \right) + i\sin \left( \sqrt{ \dfrac{2mE}{\hbar^2} } L \right) \right) + A\left( i \sqrt{\dfrac{2mE}{\hbar^2}}\right) \left( \cos \left( \sqrt{\dfrac{2mE}{\hbar^2} }L \right) -i\sin \left( \sqrt{\dfrac{2mE}{\hbar^2}}L\right) \right) \nonumber \]


