22.1.2: ii. Exercises
- Page ID
- 74208
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Q1
Replace the following classical mechanical expressions with their corresponding quantum mechanical operators.
a. K.E. = \( \frac{mv^2}{2} \) in three-dimensional space.
b. \( \textbf{p} = m\textbf{v} \), a three-dimensional Cartesian vector.
c. y-component of angular momentum: \( L_y = zp_x - xp_z. \)
Q2
Transform the following operators into the specified coordinates:
a. \( \textbf{L}_x = \dfrac{\hbar}{i}\left( y \dfrac{\partial}{\partial z} - z \dfrac{\partial}{\partial y} \right) \) from Cartesian to spherical polar coordinates.
b. \( \textbf{L}_z = \dfrac{\hbar}{i} \dfrac{\partial}{\partial \phi}\) from spherical polar to Cartesian coordinates.
Q3
Match the eigenfunctions in column B to their operators in column A. What is the eigenvalue for each eigenfunction?
\[ \begin{matrix} & \textbf{Column A} & \textbf{Column B} \\ & \text{i.} (1-x^2)\dfrac{d^2}{dx^2} - x \dfrac{d}{dx} & 4x^4 - 12x^2 + 3 \\ & \text{ii.} \dfrac{d^2}{dx^2} & 5x^4 \\ & \text{iii.} x\dfrac{d}{dx} & e^{3x} + e^{-3x} \\ & \text{iv.} \dfrac{d^2}{dx^2} - 2x\dfrac{d}{dx} & x^2 - 4x + 2 \\ \text{v.} & x\dfrac{d^2}{dx^2} + (1-x) \dfrac{d}{dx} & 4x^3 - 3x \end{matrix} \nonumber \]
Q4
Show that the following operators are Hermitian.
- \( \textbf{P}_x \)
- \( \textbf{L}_x \)
Q5
For the following basis of functions \( (\Psi_{2p_{-1'}}, \Psi_{2p_{0'}} \text{, and }\Psi_{2p_{+1}}) \), construct the matrix representation of the \(\textbf{L}_x\) operator (use the ladder operator representation of \( \textbf{L}_x \)). Verify that the matrix is Hermitian. Find the eigenvalues and corresponding eigenvectors. Normalize the eigenfunctions and verify that they are orthogonal.
\[ \Psi_{2p_{-1}} = \dfrac{1}{8\sqrt{\pi}}\sqrt{\dfrac{Z}{a}}^5 re^{\dfrac{-zr}{2a}}Sin\theta e^{-i\phi} \nonumber \]
\[ \Psi_{2p_{0}} = \dfrac{1}{\sqrt{\pi}}\sqrt{\dfrac{Z}{2a}}^5 re^{\dfrac{-zr}{2a}}Cos\theta \nonumber \]
\[ \Psi_{2p_{1}} = \dfrac{1}{8\sqrt{\pi}}\sqrt{\dfrac{Z}{a}}^5 re^{\dfrac{-zr}{2a}}Sin\theta e^{i\phi} \nonumber \]
Q6
Using the set of eigenstates (with corresponding eigenvalues) from the preceding problem, determine the probability for observing a z-component of angular momentum equal to 1\(\hbar\) if the state is given by the \(\textbf{L}_x \text{ eigenstate with 0}\hbar \textbf{ L}_x \text{ eigenvalue.}\)
Q7
Use the following definitions of the angular momentum operators:
\[ \textbf{L}_x = \dfrac{\hbar}{i}\left( y\dfrac{\partial}{\partial z} - z\dfrac{\partial}{\partial y} \right), \textbf{L}_y = \dfrac{\hbar}{i}\left( z\dfrac{\partial}{\partial x} - x\dfrac{\partial}{\partial z} \right), \textbf{L}_z = \dfrac{\hbar}{i} \left( x\dfrac{\partial}{\partial y} - y\dfrac{\partial}{\partial x} \right) \nonumber \]
\[ \text{ and } \textbf{L}^2 = \textbf{L}_x^2 + \textbf{L}_y^2 + \textbf{L}_z^2 \text{, and the relationships:} \nonumber \]
\( [\textbf{x}, \textbf{p}_x] = i\hbar \text{, [}\textbf{y}, \textbf{p}_y] = i\hbar \text{, and [}\textbf{z} , \textbf{p}_z]=i\hbar \text{, to demonstrate the following operator identities:} \)
- [\(\textbf{L}_x, \textbf{L}_y] = i\hbar \textbf{ L}_z\),
- [\(\textbf{L}_y, \textbf{L}_z] = i\hbar \textbf{ L}_x\),
- [\(\textbf{L}_z, \textbf{L}_x] = i\hbar \textbf{ L}_y\),
- [\(\textbf{L}_x, \textbf{L}^2] = 0\),
- \(\textbf{L}_y, \textbf{L}^2] = 0\),
- \(\textbf{L}_z, \textbf{L}^2] = 0\).
Q8
In exercise 7 above you determined whether or not many of the angular momentum operators commute. Now, examine the operators below along with an appropriate given function. Determine if the given function is simultaneously an eigenfunction of both operators. Is this what you expected?
a. \( \textbf{L}_z, \textbf{L}^2 \text{, with function: Y}^0_0(\theta ,\phi )= \dfrac{1}{\sqrt{4\pi}}. \)
b. \( \textbf{L}_x, \textbf{L}_z \text{, with function: Y}^0_0(\theta ,\phi )= \dfrac{1}{\sqrt{4\pi}}. \)
c. \( \textbf{L}_z, \textbf{L}^2 \text{, with function: Y}^0_1(\theta ,\phi )= \dfrac{3}{\sqrt{4\pi}}Cos \theta . \)
d. \( \textbf{L}_x, \textbf{L}_z \text{, with function: Y}^0_1(\theta ,\phi )= \dfrac{3}{\sqrt{4\pi}} Cos\theta . \)
Q9
For a "particle in a box" constrained along two axes, the wavefunction \(\Psi\)(x,y) as given in the text was:
\[ \Psi (x,y) = \sqrt{\dfrac{1}{2L_x}}\sqrt{\dfrac{1}{2L_y}}\left[ e^{\left( \dfrac{in_x\pi x}{L_x} \right)} - e^{\left(\dfrac{-in_x\pi x}{L_x}\right)} \right]\left[ e^{\left( \dfrac{in_y\pi y}{L_y} \right)} - e^{\left(\dfrac{-in_y\pi y}{L_y}\right)} \right] , \nonumber \]
with n\(_x \text{ and n}_y\) = 1,2,3, ... Show that this wavefunction is nomalized.
Q10
Using the same wavefunction, \(\Psi\)(x,y), given in exercise 9 show that the expectation value of \(\textbf{p}_x\) vanishes.
Q11
Calculate the expectation value of the x\(^2\) operator for the first two states of the harmonic oscillator. Use the v=0 and v=1 harmonic oscillator wavefunctions given below which are normalized such that \( \int\limits_{-\infty}^{\infty} \Psi (x)^2dx = 1.\) Remember that \(\Psi_0 = \sqrt[4]{\dfrac{\alpha}{\pi}} \text{e}^{\left( -\dfrac{\alpha x^2}{2}\right) } \text{ and } \Psi_1 = \sqrt[4]{\dfrac{4\alpha^3}{\pi}} x\text{e}^{\left( -\dfrac{\alpha x^2}{2}\right) } . \)
Q12
For each of the one-dimensional potential energy graphs shown below, determine:
- whether you expect symmetry to lead to a separation into odd and even solutions,
- whether you expect the energy will be quantized, continuous, or both, and
- the boundary conditions that apply at each boundary (merely stating that \( \Psi \text{ and/or } \dfrac{\partial \Psi}{\partial x} \) is continuous is all that is necessary).
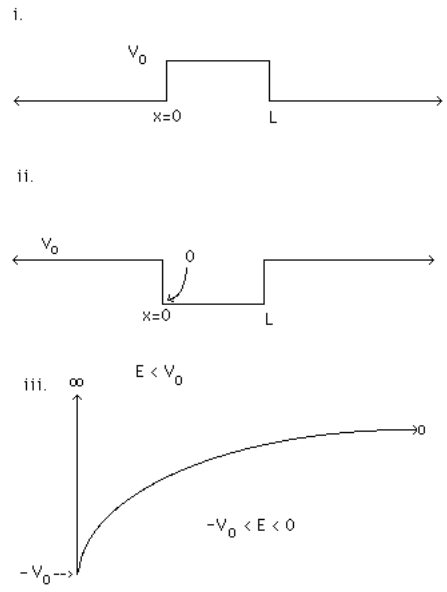
Q13
Consider a particle of mass m moving in the potential:
\[ \begin{matrix} & V(x) = \infty & \text{ for } & x < 0 & \text{ Region I } \\ & V(x) = 0 & \text{ for } & 0 \leq x \leq 0 & \text{ Region II } \\ & V(x) = V(V>0) & \text{ for } & x > L & \text{ Region III }\end{matrix} \nonumber \]
- Write the general solution to the Schrödinger equation for the regions I, II, III, assuming a solution with energy E < V (i.e. a bound state).
- Write down the wavefunction matching conditions at the interface between regions I and II and between II and III.
- Write down the boundary conditions on \(\Psi\text{ for x } \rightarrow ± \infty\).
- Use your answers to a. - c. to obtain an algebraic equation which must be satisfied for the bound state energies, E.
- Demonstrate that in the limit V \( \rightarrow \infty \), the equation you obtained for the bound state energies in d. gives the energies of a particle in an infinite box; \(E_n = \frac{n^2\hbar^2\pi^2}{2mL^2} \) ; n = 1,2,3,...


