6.1: Reduction in Symmetry Along Reaction Paths

As fragments are brought together to form a larger molecule, the symmetry of the nuclear framework (recall the symmetry of the Coulombic potential experienced by electrons depends on the locations of the nuclei) changes. However, in some cases, certain symmetry elements persist throughout the path connecting the fragments and the product molecule. These preserved symmetry elements can be used to label the orbitals throughout the 'reaction'.

The point-group, axial- and full-rotation group symmetries which arise in nonlinear molecules, linear molecules, and atoms, respectively, are seen to provide quantum numbers or symmetry labels which can be used to characterize the orbitals appropriate for each such species. In a physical event such as interaction with an external electric or magnetic field or a chemical process such as collision or reaction with another species, the atom or molecule can experience a change in environment which causes the electrostatic potential which its orbitals experience to be of lower symmetry than that of the isolated atom or molecule. For example, when an atom interacts with another atom to form a diatomic molecule or simply to exchange energy during a collision, each atom's environment changes from being spherically symmetric to being axially symmetric. When the formaldehyde molecule undergoes unimolecular decomposition to produce \(CO + H_2\) along a path that preserves \(C_{2v}\) symmetry, the orbitals of the CO moiety evolve from \(C_{2v}\) symmetry to axial symmetry.

It is important, therefore to be able to label the orbitals of atoms, linear, and nonlinear molecules in terms of their full symmetries as well in terms of the groups appropriate to lower-symmetry situations. This can be done by knowing how the representations of a higher symmetry group decompose into representations of a lower group. For example, the \(Y_{l,m}\) functions appropriate for spherical symmetry, which belong to a 2l+1 fold degenerate set in this higher symmetry, decompose into doubly degenerate pairs of functions \(Y_{l,l} , Y_{l,- l} ; Y_{l,l-1} , Y_{l,-1+1}\); etc., plus a single non-degenerate function \(Y_{l,0}\), in axial symmetry. Moreover, because \(L^2\) no longer commutes with the Hamiltonian whereas \(L_z\) does, orbitals with different l-values but the same m-values can be coupled. As the \(N_2\) molecule is formed from two N atoms, the 2s and \(2p_z\) orbitals, both of which belong to the same \((\sigma)\) symmetry in the axial rotation group but which are of different symmetry in the isolated-atom spherical symmetry, can mix to form the sg bonding orbital, the su antibonding, as well as the \(\sigma_g\) and \(\sigma_u\) nonbonding lone-pair orbitals. The fact that 2s and 2p have different l-values no longer uncouples these orbitals as it did for the isolated atoms, because l is no longer a "good" quantum number.

Another example of reduced symmetry is provided by the changes that occur as \(H_2O\) fragments into OH and H. The \(\sigma\) bonding orbitals \((a_1 \text{ and } b_2)\) and in-plane lone pair \((a_1)\) and the \(\sigma\)* antibonding \((a_1 \text{ and } b_2) \text{ of } H_2O\) become a' orbitals (see the Figure below); the out-of-plane \(b_1\) lone pair orbital becomes a'' (in Appendix IV of Electronic Spectra and Electronic Structure of Polyatomic Molecules , G. Herzberg, Van Nostrand Reinhold Co., New York, N.Y. (1966) tables are given which allow one to determine how particular symmetries of a higher group evolve into symmetries of a lower group).

Figure 6.1.1: Insert caption here!

To further illustrate these points dealing with orbital symmetry, consider the insertion of CO into \(H_2\) along a path which preserves \(C_{2v}\) symmetry. As the insertion occurs, the degenerate \(\pi\) bonding orbitals of CO become \(b1 \text{ and } b_2\) orbitals. The antibonding \(\pi\)* orbitals of CO also become \(b_1 \text{ and } b_2\). The \(\sigma_g\) bonding orbital of \(H_2 \text{ becomes } a_1\), and the \(\sigma_u \text{ antibonding } H_2 \text{ orbital becomes } b_2.\) The orbitals of the reactant \(H_2CO\) are energy-ordered and labeled according to \(C_{2v}\) symmetry in the Figure shown below as are the orbitals of the product \(H_2\) + CO.

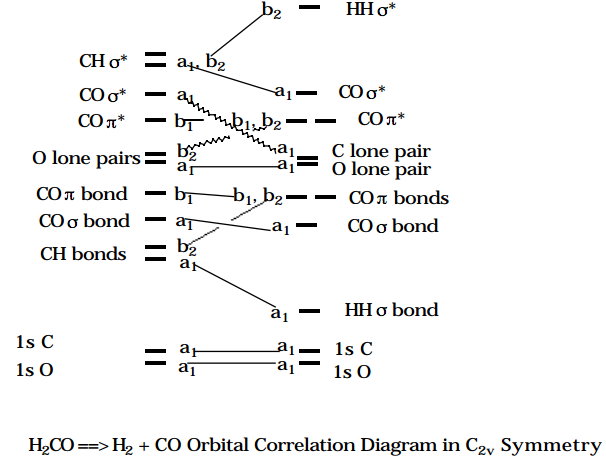
Figure 6.1.2: Insert caption here!

When these orbitals are connected according to their symmetries as shown above, one reactant orbital to one product orbital starting with the low-energy orbitals and working to increasing energy, an orbital correlation diagram (OCD) is formed. These diagrams play essential roles in analyzing whether reactions will have symmetry-imposed energy barriers on their potential energy surfaces along the reaction path considered in the symmetry analysis. The essence of this analysis, which is covered in detail in Chapter 12, can be understood by noticing that the sixteen electrons of ground-state \(H_2CO\) do not occupy their orbitals with the same occupancy pattern, symmetry-by-symmetry, as do the sixteen electrons of ground-state \(H_2\) + CO. In particular, \(H_2CO\) places a pair of electrons in the second \(b_2 \text{ orbital while } H_2 + CO\) does not; on the other hand, \(H_2\) + CO places two electrons in the sixth \(a_1 \text{ orbital while } H_2CO\) does not. The mismatch of the orbitals near the \(5a_1, 6a_1, \text{ and } 2b_2\) orbitals is the source of the mismatch in the electronic configurations of the ground-states of \(H_2CO \text{ and } H_2\) + CO. These mismatches give rise, as shown in Chapter 12, to symmetry-caused energy barriers on the \(H_2CO \rightarrow H_2 + CO\) reaction potential energy surface.