4.2: Directions of Atomic Orbitals
- Page ID
- 60558
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Atomic orbital directions also determine what directional bonds an atom will form.
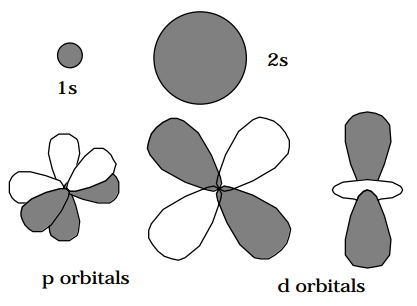
Each set of p orbitals has three distinct directions or three different angular momentum m-quantum numbers as discussed in Appendix G. Each set of d orbitals has five distinct directions or m-quantum numbers, etc; s orbitals are unidirectional in that they are spherically symmetric, and have only m = 0. Note that the degeneracy of an orbital (2l+1), which is the number of distinct spatial orientations or the number of m-values, grows with the angular momentum quantum number l of the orbital without bound.
It is because of the energy degeneracy within a set of orbitals, that these distinct directional orbitals (e.g., x, y, z for p orbitals) may be combined to give new orbitals which no longer possess specific spatial directions but which have specified angular momentum characteristics. The act of combining these degenerate orbitals does not change their energies. For example, the \(\frac{1}{\sqrt{2}}(p_x + ip_y)\) and \(\frac{1}{\sqrt{2}}(p_x - ip_y)\) combinations no longer point along the x and y axes, but instead correspond to specific angular momenta \((+1\hbar \text{ and } -1\hbar)\) about the z axis. The fact that they are angular momentum eigenfunctions can be seen by noting that the x and y orbitals contain \(\phi\) dependences of cos(\(\phi\)) and sin(\(\phi\)), respectively. Thus the above combinations contain \(e^{i\phi} \text{ and } e^{-i\phi},\) respectively. The sizes, shapes, and directions of a few s, p, and d orbitals are illustrated below (the light and dark areas represent positive and negative values, respectively).