15.9: Problems
- Page ID
- 107059
Given
\[\mathbf{A}=\begin{pmatrix} 2&3&-1 \\ -5&0&6\\ 0&2&3 \end{pmatrix}\; ;\mathbf{B}=\begin{pmatrix} 2 \\ 1\\0 \end{pmatrix}\; ;\mathbf{C}=\begin{pmatrix} 0&1\\ 2&0\\-1&3 \end{pmatrix} \nonumber\]
Multiply all possible pairs of matrices.
The matrix representation of a spin \(1/2\) system was introduced by Pauli in 1926. The Pauli spin matrices are the matrix representation of the angular momentum operator for a single spin \(1/2\) system and are defined as:
\[\mathbf{\sigma_x}=\begin{pmatrix} 0&1 \\ 1&0 \end{pmatrix}\; ;\mathbf{\sigma_y}=\begin{pmatrix} 0&-i \\ i&0 \end{pmatrix}\; ;\mathbf{\sigma_z}=\begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix} \nonumber\]
- Show that \(\mathbf{\sigma_x}\mathbf{\sigma_y}=i\mathbf{\sigma_z}\),\(\mathbf{\sigma_y}\mathbf{\sigma_z}=i\mathbf{\sigma_x}\) and \(\mathbf{\sigma_z}\mathbf{\sigma_x}=i\mathbf{\sigma_y}\)
- Calculate the commutator \(\left[\mathbf{\sigma_x},\mathbf{\sigma_y} \right]\).
- Show that \(\mathbf{\sigma_x}^2=\mathbf{\sigma_y}^2=\mathbf{\sigma_z}^2=\mathbf{I}\), where \(\mathbf{I}\) is the identity matrix. Hint: as with numbers, the square of a matrix is the matrix multiplied by itself.
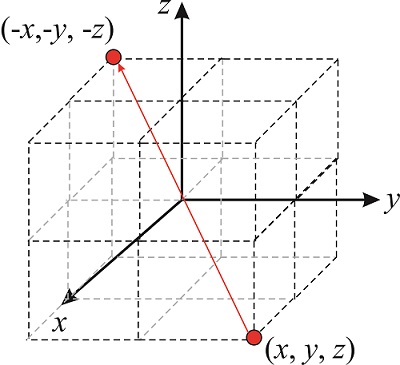
The inversion operator, \(\hat i\) transforms the point \((x,y,z)\) into \((-x,-y,-z)\). Write down the matrix that corresponds to this operator.
Calculate the inverse of \(\mathbf{A}\) by definition.
\[\mathbf{A}=\begin{pmatrix} 1&-2 \\ 0&1 \end{pmatrix} \nonumber\]
Calculate the inverse of \(\mathbf{A}\) by definition.
\[\mathbf{A}=\begin{pmatrix} \cos \theta&-\sin \theta \\ \sin \theta&\cos \theta \end{pmatrix} \nonumber\]
Find the eigenvalues and nomalized eigenvectors of
\[\mathbf{M_1}=\begin{pmatrix} 2&0 \\ 0&-3 \end{pmatrix} \nonumber\]
\[\mathbf{M_2}=\begin{pmatrix} 1&1+i \\ 1-i&1 \end{pmatrix} \nonumber\]
Given,
\[\mathbf{M_3}=\begin{pmatrix} 1&1-i \\ 1+i&1 \end{pmatrix} \nonumber\]
- Show that the matrix is Hermitian.
- Calculate the eigenvectors and prove they are orthogonal.


