8.3: The Chain Rule
- Page ID
- 106850
We all know that the position of a point in space can be specified with two coordinates, \(x\) and \(y\), called the cartesian coordinates. We also know that we can choose instead to specify the position of the point using the distance from the origin (\(r\)) and the angle that the vector makes with the \(x\) axis (\(\theta\)). The latter are what we call plane polar coordinates, which we will cover in much more detail in Chapter 10.
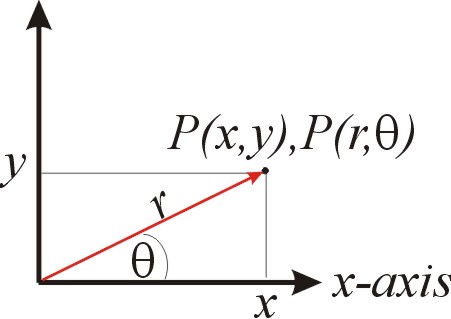
The two coordinate systems are related by:
\[\label{c2v:eq:calculus2v_cartesian} x=r\cos{\theta}; \; \;y=r\sin{\theta}\]
\[\label{c2v:eq:calculus2v_polar} r=\sqrt{x^2+y^2}; \; \; \theta=tan^{-1}(y/x)\]
Let’s assume that we are given a function in polar coordinates, for example \(f(r,\theta)=e^{-3r}\cos{\theta}\), and we are asked to find the partial derivatives in cartesian coordinates, \((\partial f/\partial x)_y\) and \((\partial f/\partial y)_x\). We can of course re-write the function in terms of \(x\) and \(y\) and find the derivatives we need, but wouldn’t it be wonderful if we had a universal formula that converts the derivatives in polar coordinates (\((\partial f/\partial r)_\theta\) and \((\partial f/\partial \theta)_r\)) to the derivatives in cartesian coordinates? This would allow us to take the derivatives in the system the equation is expressed in (which is easy), and then translate the derivatives to the other system without thinking too much. The chain rule will allow us to create these ‘universal ’ relationships between the derivatives of different coordinate systems.
Before using the chain rule, let’s obtain \((\partial f/\partial x)_y\) and \((\partial f/\partial y)_x\) by re-writing the function in terms of \(x\) and \(y\). I want to show you how much work this would involve, so you can appreciate how useful using the chain rule is. Using Equations \ref{c2v:eq:calculus2v_cartesian} and \ref{c2v:eq:calculus2v_polar}, we can rewrite \(f(r,\theta)=e^{-3r}\cos{\theta}\) as
\[f(x,y)=\dfrac{e^{-3(x^2+y^2)^{1/2}}x}{(x^2+y^2)^{1/2}} \nonumber\]
We can easily obtain \((\partial f/\partial x)_y\) and \((\partial f/\partial y)_x\), but it is certainly quite a bit of work. What if I told you that \((\partial f/\partial x)_y\) is simply
\[\label{c2v:eq:calculus2v_chain1} \left(\dfrac{\partial f}{\partial x}\right)_y=\cos{\theta}\left(\dfrac{\partial f}{\partial r}\right)_\theta-\dfrac{\sin{\theta}}{r}\left(\dfrac{\partial f}{\partial \theta}\right)_r\]
independently of the function \(f\)? We will derive this result shortly, but for now let me just mention that the procedure involves using the chain rule. You are probably sighing in relief, because the derivatives \((\partial f/\partial r)_\theta\) and \((\partial f/\partial \theta)_r\) are much easier to obtain:
\[\left(\dfrac{\partial f}{\partial r}\right)_\theta=-3e^{-3r}\cos{\theta} \nonumber\]
\[\left(\dfrac{\partial f}{\partial \theta}\right)_r=-e^{-3r}\sin{\theta} \nonumber\]
and using Equation \ref{c2v:eq:calculus2v_chain1}, we can obtain the derivative we are looking for:
\[\left(\dfrac{\partial f}{\partial x}\right)_y=-\cos{\theta}\times3e^{-3r}\cos{\theta}+\dfrac{\sin{\theta}}{r}e^{-3r}\sin{\theta} \nonumber\]
\[\left(\dfrac{\partial f}{\partial x}\right)_y=-\cos^2{\theta}\times3e^{-3r}+\dfrac{\sin^2{\theta}}{r}e^{-3r}=e^{-3r}\left(\dfrac{\sin^2{\theta}}{r}-3\cos^2{\theta}\right) \nonumber\]
\[\left(\dfrac{\partial f}{\partial x}\right)_y=e^{-3{(x^2+y^2)^{1/2}}}\left(\dfrac{y^2}{(x^2+y^2)^{3/2}}-3\dfrac{x^2}{(x^2+y^2)}\right) \nonumber\]
Hopefully this wasn’t too painful, or at least, less tedious that it would have been hadn’t we used the chain rule. What about \((\partial f/\partial y)_x\)? We can create an expression similar to Equation \ref{c2v:eq:calculus2v_chain1} and use it to relate \((\partial f/\partial y)_x\) with \((\partial f/\partial r)_\theta\) and \((\partial f/\partial \theta)_r\).
At this point you may be thinking that this all worked well because the function we had was easier to derive in polar coordinates than in cartesian coordinates. True, but this is the whole point. Many physical systems are described in polar coordinates more naturally than in cartesian coordinates (especially in three dimensions). This has to do with the symmetry of the system. For an atom, for example, it is much more natural to use spherical coordinates than cartesian coordinates. We could use cartesian, but the expressions would be much more complex and hard to work with. If we have equations that are more easily expressed in polar coordinates, getting the derivatives in polar coordinates will always be easier. But why would we want the derivatives in cartesian coordinates then? A great example is the Schrödinger equation, which is at the core of quantum mechanics. We will talk more about this when we discuss operators, but for now, the Schrödinger equation is a partial differential equation (unless the particle moves in one dimension) that can be written as:
\[E\psi(\vec{r})=-\dfrac{\hbar}{2m}\nabla^2\psi(\vec{r})+V(\vec{r})\psi{(\vec{r})} \nonumber\]
Because of the symmetry of the system, for atoms and molecules it is simpler to express the position of the particle (\(\vec{r}\)) in spherical coordinates. However, the operator \(\nabla^2\) (known as the Laplacian) is defined in cartesian coordinates as:
\[\nabla^2f(x,y,z)=\left(\dfrac{\partial^2 f}{\partial x^2}\right)_{y,z}+\left(\dfrac{\partial^2 f}{\partial y^2}\right)_{x,z}+\left(\dfrac{\partial^2 f}{\partial z^2}\right)_{x,y} \nonumber\]
In other words, the Laplacian instructs you to take the second derivatives of the function with respect to \(x\), with respect to \(y\) and with respect to \(z\), and add the three together. We could express the functions \(V(\vec{r})\) and \(\psi{(\vec{r})}\) in cartesian coordinates, but again, this would lead to a terribly complex differential equation. Instead, we can express the Laplacian in spherical coordinates, and this is in fact the best approach. To do this, we would need to relate the derivatives in spherical coordinates to the derivatives in cartesian coordinates, and this is done using the chain rule.
Hopefully all this convinced you of the uses of the chain rule in the physical sciences, so now we just need to see how to use it for our purposes. In two dimensions, the chain rule states that if we have a function in one coordinate system \(u(x,y)\), and these coordinates are functions of two other variables (e.g. \(x=x(\theta,r)\) and \(y=y(\theta,r)\)) then:
\[\left ( \dfrac{\partial u}{\partial r} \right )_\theta=\left ( \dfrac{\partial u}{\partial x} \right )_y\left ( \dfrac{\partial x}{\partial r} \right )_\theta+\left ( \dfrac{\partial u}{\partial y} \right )_x\left ( \dfrac{\partial y}{\partial r} \right )_\theta\]
\[\left ( \dfrac{\partial u}{\partial \theta} \right )_r=\left ( \dfrac{\partial u}{\partial x} \right )_y\left ( \dfrac{\partial x}{\partial \theta} \right )_r+\left ( \dfrac{\partial u}{\partial y} \right )_x\left ( \dfrac{\partial y}{\partial \theta} \right )_r\]
Some students find the following ’tree’ constructions useful:

We can also consider \(u=u(r,\theta)\), and \(\theta=\theta(x,y)\) and \(r=r(x,y)\), which gives:
\[\left ( \dfrac{\partial u}{\partial x} \right )_y=\left ( \dfrac{\partial u}{\partial r} \right )_\theta\left ( \dfrac{\partial r}{\partial x} \right )_y+\left ( \dfrac{\partial u}{\partial \theta} \right )_r\left ( \dfrac{\partial \theta}{\partial x} \right )_y\]
\[\left ( \dfrac{\partial u}{\partial y} \right )_x=\left ( \dfrac{\partial u}{\partial r} \right )_\theta\left ( \dfrac{\partial r}{\partial y} \right )_x+\left ( \dfrac{\partial u}{\partial \theta} \right )_r\left ( \dfrac{\partial \theta}{\partial y} \right )_x\]
Derive Equation \ref{c2v:eq:calculus2v_chain1}.
Solution
We need to prove \(\left(\dfrac{\partial f}{\partial x}\right)_y=\cos{\theta}\left(\dfrac{\partial f}{\partial r}\right)_\theta-\dfrac{\sin{\theta}}{r}\left(\dfrac{\partial f}{\partial \theta}\right)_r\). Using the chain rule:
\[\left ( \dfrac{\partial f}{\partial x} \right )_y=\left ( \dfrac{\partial f}{\partial \theta} \right )_r\left ( \dfrac{\partial \theta}{\partial x} \right )_y+\left ( \dfrac{\partial f}{\partial r} \right )_\theta\left ( \dfrac{\partial r}{\partial x} \right )_y \nonumber\]
From Equation \ref{c2v:eq:calculus2v_cartesian} and \ref{c2v:eq:calculus2v_polar}
\[\left ( \dfrac{\partial r}{\partial x} \right )_y=\dfrac{1}{2}(x^2+y^2)^{-1/2}(2x)=\dfrac{1}{2}(r^2)^{-1/2}(2r\cos{\theta})=\cos{\theta} \nonumber\]
\[\left ( \dfrac{\partial \theta}{\partial x} \right )_y=\dfrac{1}{1+(y/x)^2}\dfrac{(-y)}{x^2}=-\dfrac{1}{1+(y/x)^2}\dfrac{y}{x}\dfrac{1}{x}=-\dfrac{1}{1+\tan^2{\theta}}\tan{\theta}\dfrac{1}{r\cos{\theta}}=-\dfrac{1}{1+\dfrac{\sin^2{\theta}}{\cos^2{\theta}}}\dfrac{\sin{\theta}}{\cos{\theta}}\dfrac{1}{r\cos{\theta}}=-\dfrac{\sin{\theta}}{r} \nonumber\]
Therefore,
\[\left ( \dfrac{\partial f}{\partial x} \right )_y=\cos{\theta}\left ( \dfrac{\partial f}{\partial r} \right )_\theta-\dfrac{\sin{\theta}}{r}\left ( \dfrac{\partial f}{\partial \theta} \right )_r \nonumber\]
Need help? The videos below contain examples of how to use the chain rule for partial derivatives:
- Example 1: http://www.youtube.com/watch?v=HOYA0-pOHsg
- Example 2: http://www.youtube.com/watch?v=kCr13iTRN7E (tree diagrams)


