3.3: Taylor Series
- Page ID
- 106815
Before discussing more applications of Maclaurin series, let’s expand our discussion to the more general case where we expand a function around values different from zero. Let’s say that we want to expand a function around the number \(h\). If \(h=0\), we call the series a Maclaurin series, and if \(h\neq0\) we call the series a Taylor series. Because Maclaurin series are a special case of the more general case, we can call all the series Taylor series and omit the distinction. The following is true for a function \(f(x)\) as long as the function and all its derivatives are finite at \(h\):
\[\label{taylor} f(x)=a_0 + a_1(x-h)+a_2(x-h)^2+...+a_n(x-h)^n = \displaystyle\sum_{n=0}^{\infty}a_n(x-h)^n\]
The coefficients are calculated as
\[\label{taylorcoeff} a_n=\frac{1}{n!}\left( \frac{d^n f}{dx^n}\right)_h\]
Notice that instead of evaluating the function and its derivatives at \(x=0\) we now evaluate them at \(x=h\), and that the basis set is now \(1, (x-h), (x-h)^2,...,(x-h)^n\) instead of \(1, x, x^2,...,x^n\). A Taylor series will be a good approximation of the function at values of \(x\) close to \(h\), in the same way Maclaurin series provide good approximations close to zero.
To see how this works let’s go back to the exponential function. Recall that the Maclaurin expansion of \(e^x\) is shown in Equation \(3.1.3\). We know what happens if we expand around zero, so to practice, let’s expand around \(h=1\). The coefficient \(a_0\) is \(f(1)= e^1=e\). All the derivatives are \(e^x\), so \(f'(1)=f''(1)=f'''(1)...=e.\) Therefore, \(a_n=\frac{e}{n!}\) and the series is therefore
\[\label{taylorexp} e\left[ 1+(x-1)+\frac{1}{2}(x-1)^2+\frac{1}{6}(x-1)^3+... \right]=\displaystyle\sum_{n=0}^{\infty}\frac{e}{n!}(x-1)^n\]
We can use the same arguments we used before to conclude that \(e^x\approx ex\) if \(x\approx 1\). If \(x\approx 1\), \((x-1)\approx 0\), and the terms \((x-1)^2, (x-1)^3\) will be smaller and smaller and will contribute less and less to the sum. Therefore,
\[e^x \approx e \left[ 1+(x-1) \right]=ex.\]
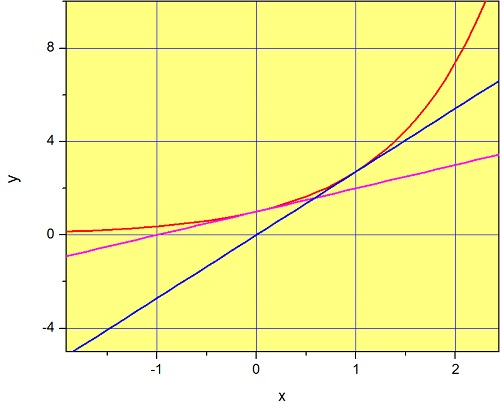
This is the equation of a straight line with slope \(e\) and \(y\)-intercept 0. In fact, from Equation \(3.1.7\) we can see that all functions will look linear at values close to \(h\). This is illustrated in Figure \(\PageIndex{1}\), which shows the exponential function (red) together with the functions \(1+x\) (magenta) and \(ex\) (blue). Not surprisingly, the function \(1+x\) provides a good approximation of \(e^x\) at values close to zero (see Equation \(3.1.3\)) and the function \(ex\) provides a good approximation around \(x=1\) (Equation \ref{taylorexp}).
Expand \(f(x)=\ln{x}\) about \(x=1\)
Solution
\[f(x)=a_0 + a_1(x-h)+a_2(x-h)^2+...+a_n(x-h)^n, a_n=\frac{1}{n!}\left( \frac{d^n f}{dx^n}\right)_h \nonumber\]
\[a_0=f(1)=\ln(1)=0 \nonumber\]
The derivatives of \(\ln{x}\) are:
\[f'(x) = 1/x, f''(x)=-1/x^2, f'''(x) = 2/x^3, f^{(4)}(x)=-6/x^4, f^{(5)}(x)=24/x^5... \nonumber\]
and therefore,
\[f'(1) = 1, f''(1)=-1, f'''(1) = 2, f^{(4)}(1)=-6, f^{(5)}(1)=24.... \nonumber\]
To calculate the coefficients, we need to divide by \(n!\):
- \(a_1=f'(1)/1!=1\)
- \(a_2=f''(1)/2!=-1/2\)
- \(a_3=f'''(1)/3!=2/3!=1/3\)
- \(a_4=f^{(4)}(1)/4!=-6/4!=-1/4\)
- \(a_n=(-1)^{n+1}/n\)
The series is therefore:
\[f(x)=0 + 1(x-1)-1/2 (x-1)^2+1/3 (x-1)^3...=\displaystyle{\color{Maroon}\displaystyle\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n}(x-1)^{n}} \nonumber\]
Note that we start the sum at \(n=1\) because \(a_0=0\), so the term for \(n=0\) does not have any contribution.
Need help? The links below contain solved examples.
External links:
Finding the Taylor series of a function I: http://patrickjmt.com/taylor-and-maclaurin-series-example-2/


