3.4C: Using the Minimum Amount of Hot Solvent
- Page ID
- 95757
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The quantity of solvent used in crystallization is usually kept to a minimum, to support the goal of recovering the maximum amount of crystals.
Every solid has partial solubility in the solvents used, even at cold temperatures. In Figure 3.19 the cold solvent surrounding a yellow solid is tinted yellow as some compound dissolves. Solids that appear insoluble in a solvent do in fact have a (normally small) portion of material that dissolves. This is analogous to how "water-insoluble" ionic compounds (such as \(\ce{AgCl}\) have a non-zero solubility product constant \(\left( K_\text{sp} \right)\).

Crystallization is most common with solids that have moderate solubility at low temperatures, so that heat can "tip them over the edge" to completely dissolve. This means that in practice there will be a quantity of compound that dissolves in the mother liquor at low temperatures, which can be significant depending on the compound's solubility profile. Use of the minimal amount of hot solvent lessens the quantity of compound that is lost to the mother liquor.
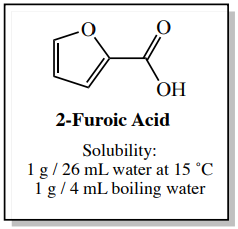
To demonstrate the importance of using the minimum amount of hot solvent during a crystallization, imagine you are to crystallize \(5.0 \: \text{g}\) 2-furoic acid using hot water.\(^8\) The calculations from this example are described below, and summarized in Figure 3.21.
2-furoic acid has an increased solubility in boiling water compared to cold water, as shown by the solubility data in Figure 3.20. The quantity of hot solvent needed to dissolve this sample can be calculated using the compound's solubility in hot water, as shown below. This represents the "minimum amount of hot solvent" needed for the crystallization.
\[5.0 \: \text{g 2-furoic acid (FA)} \times \frac{4 \: \text{mL hot water}}{1 \: \text{g FA}} = \textbf{20. mL hot water}\]
When the 2-furoic acid is dissolved in \(20 \: \text{mL}\) of hot water and is allowed to cool, the compound will crystallize as it has a lower solubility in the cold solvent. Ideally the solution would be placed in an ice bath \(\left( 0^\text{o} \text{C} \right)\), but as \(0^\text{o} \text{C}\) solubility data is not provided, let's imagine the solution is cooled to \(15^\text{o} \text{C}\). The solubility of 2-furoic acid in this cold water is as follows.
\[20. \: \text{mL cold water} \times \frac{1 \: \text{g FA}}{26 \: \text{mL cold water}} = \textbf{0.77 g FA} \: \text{dissolves in } 15^\text{o} \text{C} \: \text{water}\]
This calculation shows that a portion of the 2-furoic acid will remain dissolved in the mother liquor even when placed in the cold bath. Any compound present that exceeds this quantity will crystallize, in this case \(4.2 \: \text{g}\) of 2-furoic acid \(\left( 5.0 \: \text{g} - 0.77 \: \text{g} \right)\). Note that because of the loss of material to the mother liquor, the maximum theoretical recovery from this process is only \(84\%\) \(\left( 100 \times 4.2 \: \text{g}/5.0 \: \text{g} \right)\).

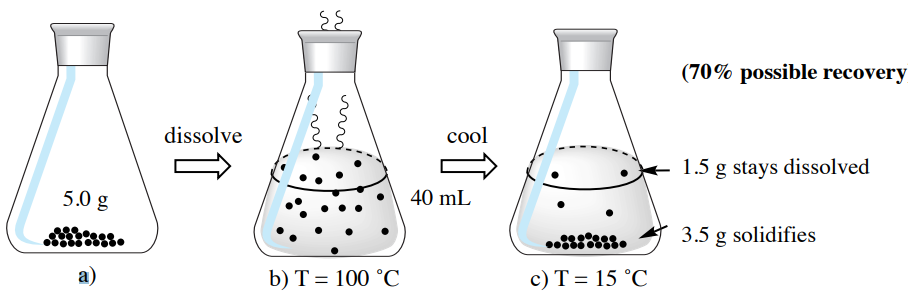
Next imagine that instead of using the minimum amount of hot solvent, we use double the volume of hot solvent (\(40 \: \text{mL}\) in this example). The calculations from this example are described below, and summarized in Figure 3.22.
When the solvent volume is doubled, the quantity of material dissolved in the mother liquor also doubles, as shown in the calculation below.
\[40. \: \text{mL cold water} \times \frac{1 \: \text{g FA}}{26 \: \text{mL cold water}} = \textbf{1.5 g FA} \: \text{dissolves in } 15^\text{o} \text{C} \: \text{water}\]
If a \(5.0 \: \text{g}\) sample of 2-furoic acid were instead dissolved in \(40 \: \text{mL}\) (double the minimal amount of hot solvent necessary), only \(3.5 \: \text{g}\) would crystallize \(\left( 5.0 \: \text{g} - 1.5 \: \text{g} \right)\). The maximum theoretical recovery for this process is only \(70\%\).
Notice when additional solvent is used than the minimum, more compound is soluble in the solvent and lost to the mother liquor, leading to a lower theoretical recovery.
As you might imagine, there is also a quantity of solvent in which the entire \(5.0 \: \text{g}\) sample of 2-furoic acid dissolves (in this case \(130 \: \text{mL}\), see calculation below). If \(130 \: \text{mL}\) were used for the crystallization instead of the minimal amount of hot solvent, no crystals would form at all when cooled to \(15^\text{o} \text{C}\) (\(0\%\) recovery). Thus the quantity of solvent used in crystallization should be monitored and restricted when possible.
\[5.0 \: \text{g FA (2-furoic acid)} \times \frac{26 \: \text{mL cold water}}{1 \: \text{g FA}} = \textbf{130 mL} \: \text{of } 15^\text{o} \text{C} \: \text{water dissolves the whole sample}\]
To demonstrate the importance of using the minimum amount of hot solvent, two samples of benzil (each roughly \(1.8 \: \text{g}\)), were crystallized from hot ethanol (Figure 3.23). The first was dissolved in the minimum amount of hot solvent (approximately \(8 \: \text{mL}\)), and resulted in a \(92\%\) recovery after crystallization. The second was dissolved in roughly double the quantity of hot solvent (approximately \(15 \: \text{mL}\)) and resulted in an \(87\%\) recovery. The solubility profile of benzil led to an excellent recovery in both trials, but the recovery was compromised somewhat when an excess of solvent was used.

\(^8\)As recommended in D.D. Perrin, W.L.F. Armarego, Purification of Organic Chemicals, Pergamon Press, 3\(^\text{rd}\) edition, 1988.


