2.3D: Separation Theory
- Page ID
- 93520
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)General Theory
TLC is an excellent analytical tool for separating mixtures in a sample. In this section are discussed the details of the separation, and expand upon the general discussion of Section 2.1.B.
In all forms of chromatography, samples equilibrate between stationary and mobile phases. In almost all applications of TLC, the stationary phase is a silica or alumina adsorbent and the mobile phase is an organic solvent or solvent mixture (the "eluent") that rises up the plate (equation 3).
\[\ce{X}_\text{(silica/alumina)} \rightleftharpoons \ce{X}_\text{(solvent)} \label{3}\]
Silica gel (shown in Figure 2.16) is composed of a network of silicon-oxygen bonds, with \(\ce{O-H}\) bonds on its surface, as well as a layer of water molecules. Silica gel \(\left( \ce{SiO_2} \cdot x \ce{H_2O} \right)\) is used in this discussion, but is structurally analogous to alumina \(\left( \ce{Al_2O_3} \cdot x \ce{H_2O} \right)\). This very polar stationary phase is paired with a relatively nonpolar mobile phase (an organic solvent or solution), in what is referred to as "normal phase" TLC. Although this is the most common form of TLC (and what will be focused on in this section), "reverse phase" TLC (with a nonpolar stationary phase and a polar mobile phase) is sometimes used.
Figure 2.16 shows how acetophenone would cling to the surface of silica gel through intermolecular forces (IMF's). In this case, acetophenone can hydrogen bond (the IMF indicated in Figure 2.16a) to the silica surface through its oxygen atom. As eluent flows over the sample (Figure 2.16b), an equilibrium is established between the sample being adsorbed on the stationary phase and dissolved in the mobile phase. When in the mobile phase, the compound moves up the plate with the flow of liquid (Figure 2.16c) to later readsorb on the stationary phase further up the plate. The resulting \(R_f\) of the compound is dependent on the amount of time spent in the stationary and mobile phases.
.png?revision=1&size=bestfit&width=1110&height=395)
The equilibrium distribution between the two phases depends on several factors:
- It depends on the strength of intermolecular forces between the sample and the stationary phase.
A compound that forms strong IMF's with the silica or alumina will often favor the stationary phase, and will spend much of the elution time adhered to the plate. This means it will spend less time in the mobile phase (which is the only means for it to travel up the plate), causing it to end up low on the TLC plate, and have a low \(R_f\).
Compounds that have oxygen or nitrogen atoms should be able to hydrogen bond with the stationary phase (have strong IMF's with the stationary phase), and thus will have lower \(R_f\) values than compounds of similar size that can only interact through London dispersion forces (LDF's). - It depends on the strength of interaction between the sample and the mobile phase.
As the mobile phase is always less polar than the stationary phase in normal phase TLC, polar compounds will tend to have a lesser affinity for the mobile phase than nonpolar compounds (based on the "like dissolves like" principle). Therefore, polar compounds tend to spend less of the elution time mobile than a nonpolar compound, so will travel "slower" up the plate, and have a low \(R_f\).
The degree of attraction by a compound to the stationary and mobile phases lead to the same conclusion:
- The stronger IMF's possible with the stationary phase (often the more polar functional groups on a compound), the more time the compound will be stationary \(\rightarrow\) lower \(R_f\).
- The more polar functional groups present on a compound, the less it tends to be attracted to the less polar eluent, and the less time the compound will be mobile \(\rightarrow\) lower \(R_f\).
Thus, a compound with a lower \(R_f\) tends to have more polar functional groups than a compound with a higher \(R_f\) (summarized in Figure 2.17).
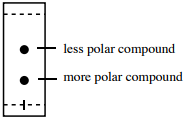
Structural Considerations
To demonstrate the effect of structural features on \(R_f\), an eluted TLC plate of benzyl alcohol, benzaldehyde, and ethylbenzene is shown in Figure 2.18. The relative order of \(R_f\) reflects the polarity trend in the series.
.png?revision=1&size=bestfit&width=889&height=413)
Benzyl alcohol and benzaldehyde have polar functional groups so thus had lower \(R_f\) values than ethylbenzene, which is completely nonpolar. Both compounds are able to hydrogen bond to the polar stationary phase (Figure 2.19a+b), so are more strongly attracted to the stationary phase than ethylbenzene, which interacts only through weak London dispersion forces (Figure 2.19c). As the least "polar" of the series, ethylbenzene is also the best dissolved by the weakly polar eluent. For these reasons, ethylbenzene spent the least time in the stationary phase and the most time in the mobile phase, which is why it traveled the furthest up the plate and had the highest \(R_f\) of the series.
.png?revision=1&size=bestfit&width=1096&height=446)
Both benzaldehyde and benzyl alcohol are capable of hydrogen bonding with the stationary phase, but benzyl alcohol had the lower \(R_f\) because it can form more hydrogen bonds (through both the oxygen and hydrogen atoms of the \(\ce{OH}\) group, Figure 2.19a). This caused benzyl alcohol to be more strongly adhered to the silica/alumina than benzaldehyde, causing it to spend more time in the stationary phase.
To demonstrate a different structural effect on \(R_f\), an eluted TLC plate of acetophenone and benzophenone is shown in Figure 2.20. Both compounds are similar in that they can hydrogen bond to the stationary phase through their oxygen atom. However, the larger size of benzophenone causes it to have a slightly higher \(R_f\) than acetophenone.
.png?revision=1&size=bestfit&width=1103&height=424)
This result can be explained in multiple ways:
- The oxygen atom in benzophenone is more crowded by the aromatic rings than the oxygen atom of acetophenone, which may impede its ability to strongly hydrogen bond with the silica gel. This can lead to a smaller amount of time adsorbed by the stationary phase.
- The additional nonpolar bulk of benzophenone makes it dissolve better in the weakly polar eluent, causing it to spend more time in the mobile phase.
Mobile Phase Polarity
The ability of chromatography to separate components in a mixture depends on equilibration of a compound between the stationary and mobile phases. Since the mobile phase is an important factor, it is possible to change the \(R_f\) of a compound by changing the polarity of the mobile phase.
When a mobile phase is made more polar than originally, all compounds travel further and have a higher \(R_f\).
This general trend is demonstrated in Figure 2.21b+c, where the TLC of three UV-active compounds (lanes 2-4) was run using two different mixed solvents. The first plate was run using a 6:1 hexane:ethyl acetate mixture, which means the solvent was created by using 6 volumes of hexane for every 1 volume of ethyl acetate. This mixed solvent is mostly nonpolar due to the high percentage of hexane, but is more polar than straight hexane, due to the presence of some ethyl acetate (which has polar bonds, Figure 2.21a). The second plate was run using a 3:2 hexane:ethyl acetate mixture, which is more polar than the 6:1 mixture because there is a higher percentage of ethyl acetate present.
.png?revision=1&size=bestfit&width=602&height=339)
| Lane | \(R_f\) in 6:1 (less polar eluent) | \(R_f\) in 3:2 (more polar eluent) |
|---|---|---|
| 2 | 0.33 | 0.54 |
| 3 (bottom spot) | 0.02 | 0.17 |
| 3 (top spot) | 0.28 | 0.52 |
| 4 | 0.49 | 0.65 |
Note that in Figure 2.21c all spots maintained their relative order but traveled to a greater height on the plate and increased their \(R_f\) values (Table 2.2) in the more polar eluent.
An increase in solvent polarity increases \(R_f\) values for two reasons:
- Moderately polar compounds have a greater attraction to the mobile phase.
When equilibrating between a polar stationary phase and nonpolar eluent, a polar compound tends to favor the polar stationary phase and have a low \(R_f\). If the eluent is made to be moderately polar, polar compounds are then more attracted to the mobile phase, causing the equilibrium to change such that the compound spends more time in the mobile phase, resulting in a higher \(R_f\). - The polar solvent may occupy binding sites on the silica or alumina surface, such that they displace the sample from the stationary phase.
If a polar solvent is able to hydrogen bond and therefore strongly associated with the stationary phase, it may "lock up" binding sites, and force less polar compounds to spend more time in the mobile phase. The result is an increased \(R_f\) for polar and nonpolar compounds alike.


