3.9: Spin-Spin Splitting and Molecular Asymmetry

An interesting and unusual splitting is sometimes observed when a -CH₂-Y group is attached to another carbon atom, carrying three different groups.⁸ An excellent example is methyl 2,3-dibromo-2- methylpropionate, the proton NMR spectrum of which is shown in Fig.3-11. Besides the large three-proton resonance peaks of the ester and the \(\alpha\) methyls there are four small peaks which fit the typical pattern of two nonequivalent protons, splitting each other with a coupling constant of about the same magnitude as the chemical shift. All chemical experience indicates that the rate of rotation of the groups with respect to one another around the 2,3-carbon-carbon single bond in this molecule should be reasonably rapid. However, there is good evidence that substituted ethanes of this type are more stable in the staggered conformations, as shown in Fig. 3-12.

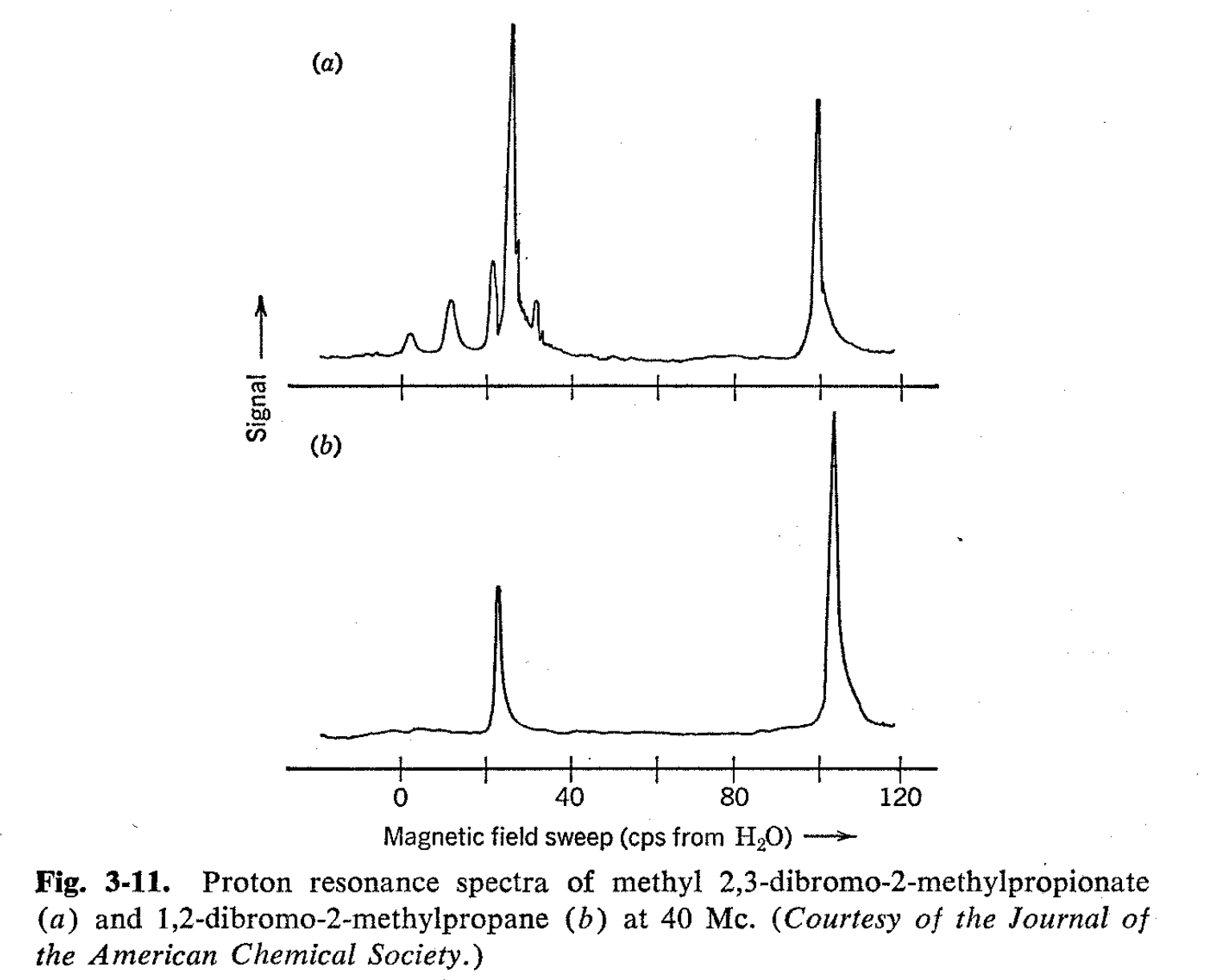
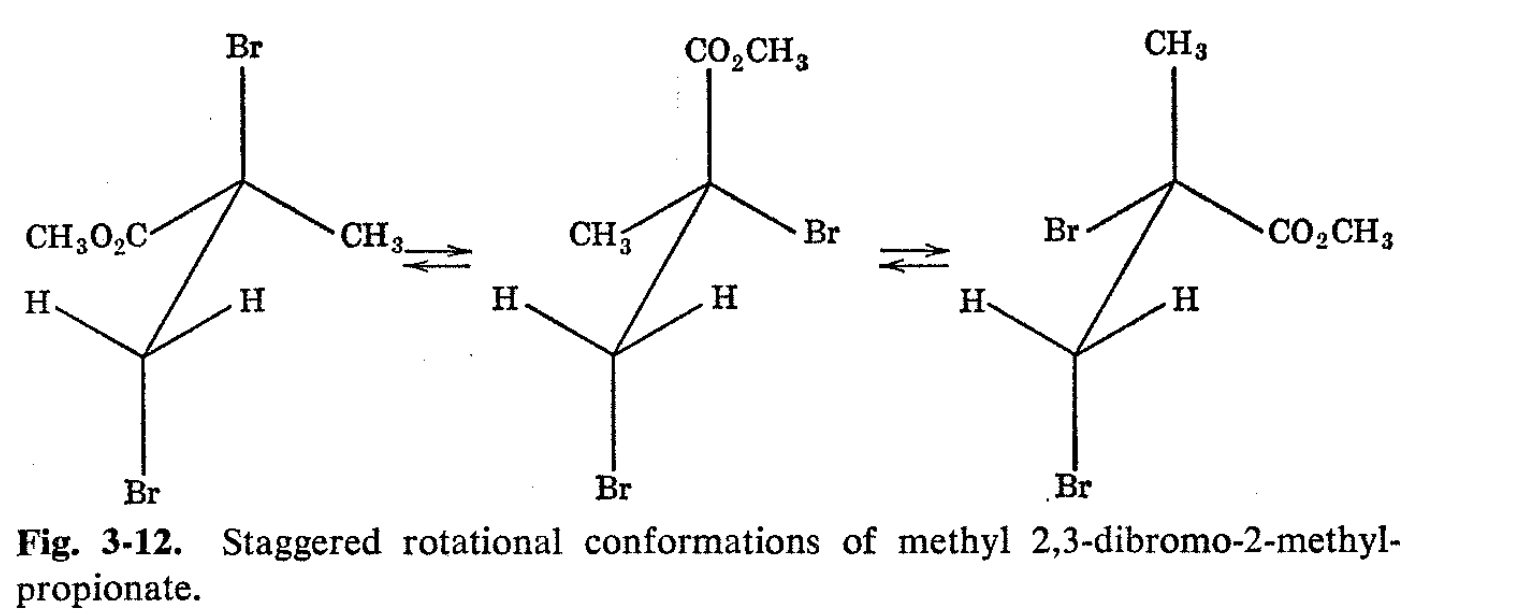
In the present case, inspection of the various staggered conformations shows that the \(\beta\)-methylene hydrogens are not equivalently located in any one of them with respect to the groups attached to the carbon. Therefore, there must be at least some degree of nonequivalence of the \(\beta\) protons, and spin-spin splitting is consequently possible. At present, it is not known to what extent the relative residence times of the molecules in particular conformations are important in determining the degree of nonequivalence. If all the conformations had equal residence times and rapid rotation occurred, then each hydrogen would experience nearly the same average magnetic field. On the other hand, if the residence times were quite different, then the average magnetic field would be much like that of the most favored conformation and a larger degree of nonequivalence would be expected.

Ethanes with -CH₂-Y attached to -CX₂Y are not expected to show nonequivalent protons if rotation is rapid around the C-C bond. Thus, inspection of the possible staggered conformations for 1,2-dibromo-2- methylpropane (see Fig. 3-13) shows that the conformation with the bromines trans to one another has a plane of symmetry and the methylene hydrogens are thereby automatically equivalent. The other two conformations have nonequivalent protons, but since they are mirror images of each other, the protons will spend equal time in each.

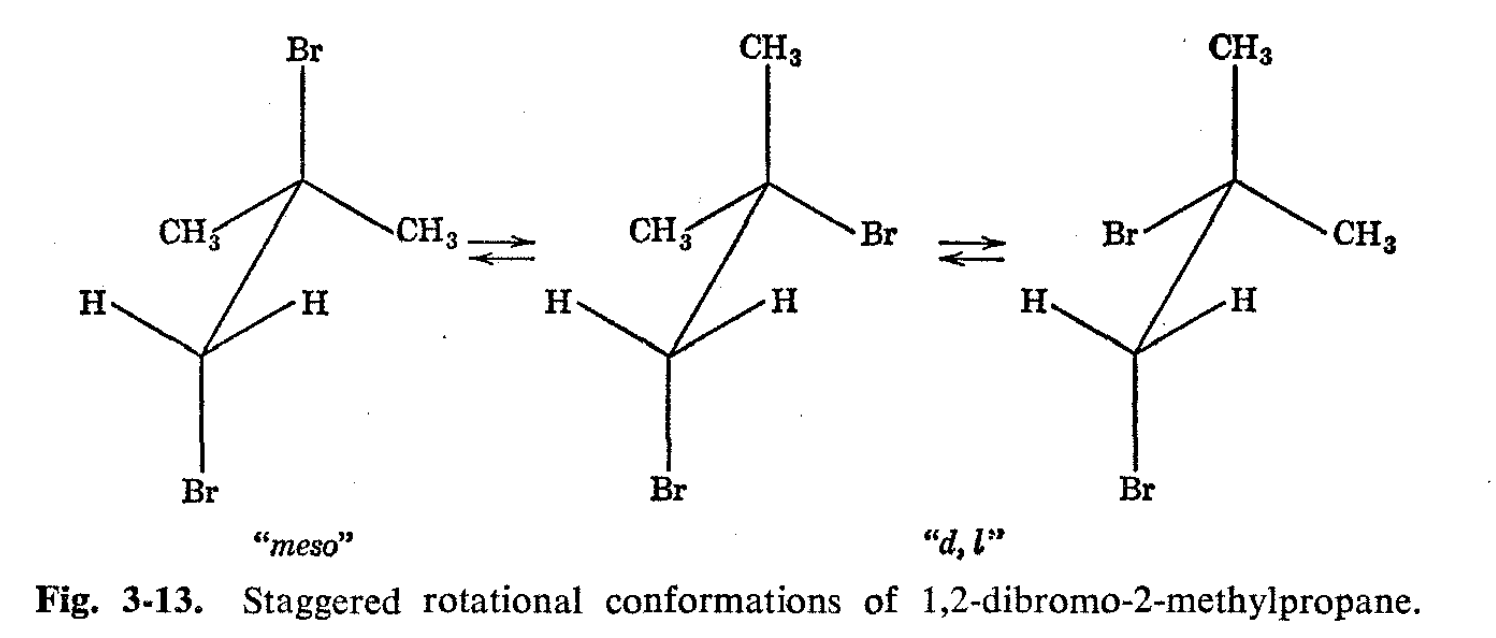
Therefore, if all the forms are interconverted rapidly, the two methylene protons will reside in identical average environments (cf. spectrum in Fig. 3-1 1). As will be seen later, slow rotation about the C-C bond in substances of this type will lead to more complex spectra because then the magnetic environments of the individual methylene protons are not identical in all the conformations.

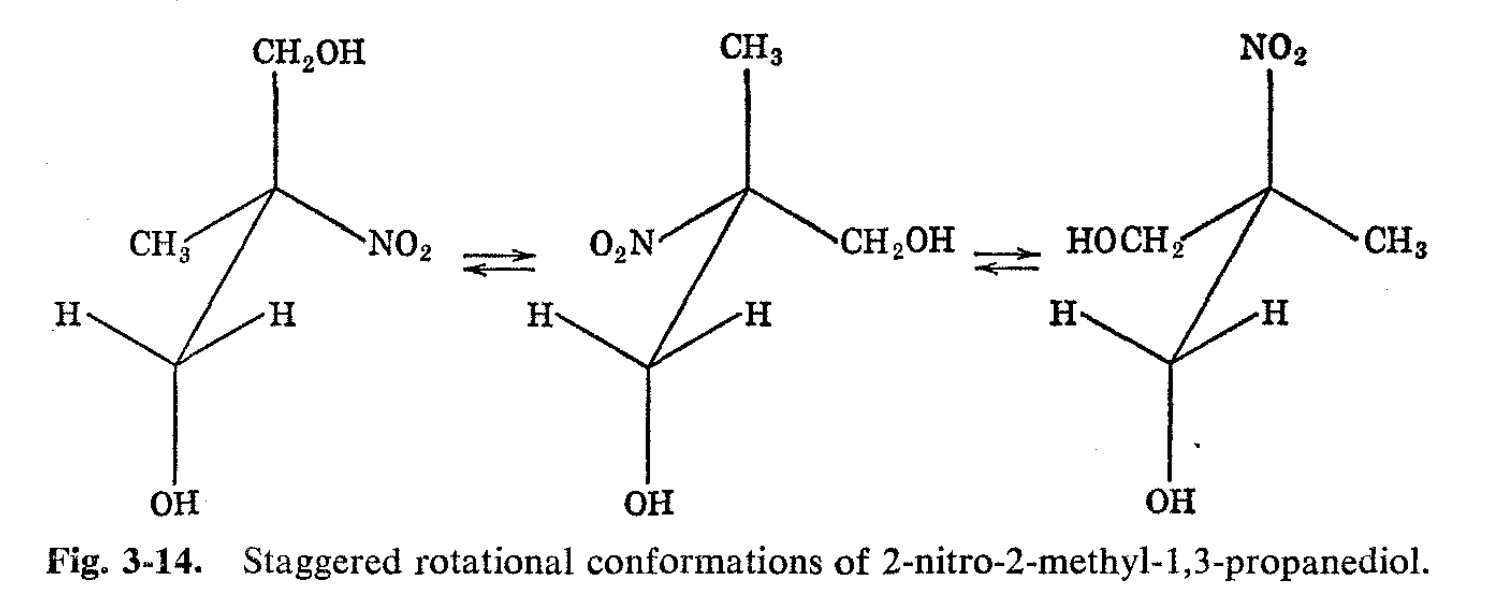
The type of spin-spin splitting observed for methyl 2,3-bromo-2- methylpropionate appears to offer a new approach to detecting asymmetric centers in organic molecules without recourse to resolution into optical antipodes. Strictly, the method provides a test for a carbon with three different groups attached rather than a test for molecules which might be resolvable into optical antipodes. Thus, 2-nitro-2-methyl-1,3- propanediol is not capable of being resolved into optical antipodes but shows nonequivalent methylene protons because each methylene is attached to an asymmetric group (see Fig. 3-14). A comprehensive theoretical treatment of various types of asymmetric molecules has been made by Pople.⁹

---

8 P. M. Nair and J. D. Roberts, J. Am. Chem. Soc., 79, 4565 (1957).

9 J. A. Pople, Molecular Physics, 1, 3 (1958).