6.5: Meso Compounds
- Page ID
- 45162
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objective
- recognize and classify meso compounds
A meso compound is an achiral compound that has chiral centers. It is superimposed on its mirror image and is optically inactive although it contains two or more stereocenters.
Introduction
In general, a meso compound should contain two or more identical substituted stereocenters. Also, it has an internal symmetry plane that divides the compound in half. These two halves reflect each other by the internal mirror. The stereochemistry of stereocenters should "cancel out". What it means here is that when we have an internal plane that splits the compound into two symmetrical sides, the stereochemistry of both left and right side should be opposite to each other, and therefore, result in optically inactive. Cyclic compounds may also be meso.
Identification
If A is a meso compound, it should have two or more stereocenters, an internal plane, and the stereochemistry should be R and S.
- Look for an internal plane, or internal mirror, that lies in between the compound.
- The stereochemistry (e.g. R or S) is very crucial in determining whether it is a meso compound or not. As mentioned above, a meso compound is optically inactive, so their stereochemistry should cancel out. For instance, R cancels S out in a meso compound with two stereocenters.
.bmp?revision=1)
trans-1,2-dichloro-1,2-ethanediol
.bmp?revision=1)
(meso)-2,3-dibromobutane
Tips: An interesting thing about single bonds or sp3-orbitals is that we can rotate the substituted groups that attached to a stereocenter around to recognize the internal plane. As the molecule is rotated, its stereochemistry does not change. For example:
.bmp?revision=1)
Another case is when we rotate the whole molecule by 180 degree. Both molecules below are still meso.
Remember the internal plane here is depicted on two dimensions. However, in reality, it is three dimensions, so be aware of it when we identify the internal mirror.
Example \(\PageIndex{1}\):
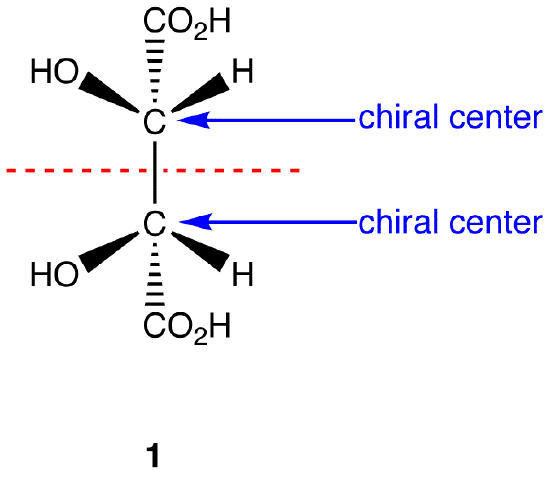
1 has a plane of symmetry (the horizontal plane going through the red broken line) and, therefore, is achiral; 1 has chiral centers. Thus, 1 is a meso compound.
Example \(\PageIndex{2}\):
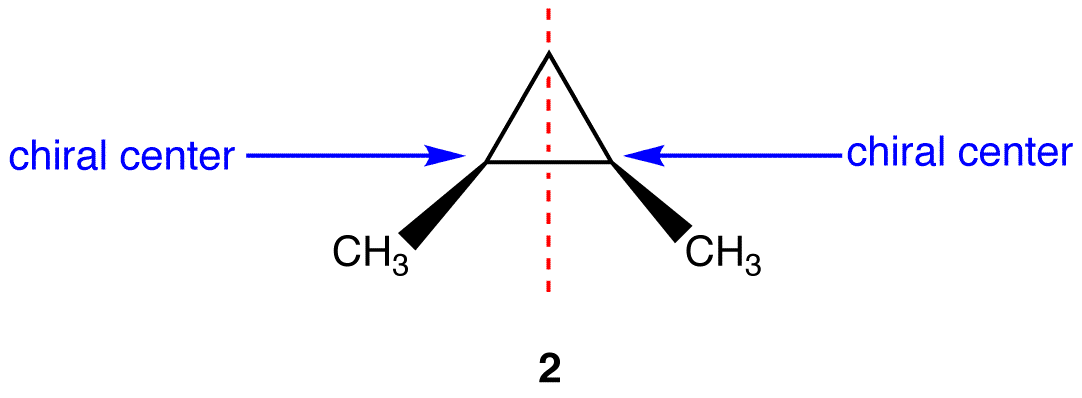
This molecules has a plane of symmetry (the vertical plane going through the red broken line perpendicular to the plane of the ring) and, therefore, is achiral, but has has two chiral centers. Thus, its is a meso compound.
Exercise \(\PageIndex{1}\)
Which of the following are meso-compounds:
- C – 2,3-dibromobutane
- D – 2,3-dibromopentane
- Answer
-
Compounds A and C are meso.
Other Examples of meso compounds
Meso compounds can exist in many different forms such as pentane, butane, heptane, and even cyclobutane. They do not necessarily have to be two stereocenters, but can have more.
.bmp?revision=1)
The chiral centers in the preceding examples have all been different. In the case of 2,3-dihydroxybutanedioic acid, known as tartaric acid, the two chiral centers have the same four substituents and are equivalent. As a result, two of the four possible stereoisomers of this compound are identical due to a plane of symmetry, so there are only three stereoisomeric tartaric acids. Two of these stereoisomers are enantiomers and the third is an achiral diastereomer, called a meso compound. Meso compounds are achiral (optically inactive) diastereomers of chiral stereoisomers. Investigations of isomeric tartaric acid salts, carried out by Louis Pasteur in the mid 19th century, were instrumental in elucidating some of the subtleties of stereochemistry. Some physical properties of the isomers of tartaric acid are given in the following table.
| (+)-tartaric acid: | [α]D = +13º | m.p. 172 ºC |
| (–)-tartaric acid: | [α]D = –13º | m.p. 172 ºC |
| meso-tartaric acid: | [α]D = 0º | m.p. 140 ºC |
Fischer projection formulas provide a helpful view of the configurational relationships within the structures of these isomers. In the following illustration a mirror line is drawn between formulas that have a mirror-image relationship. In demonstrating the identity of the two meso-compound formulas, remember that a Fischer projection formula may be rotated 180º in the plane.
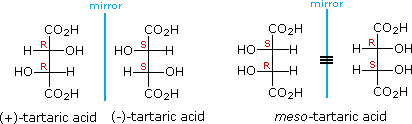
Optical Activity Analysis
When the optical activity of a meso compound is attempted to be determined with a polarimeter, the indicator will not show (+) or (-). It simply means there is no certain direction of rotation of the polarized light, neither levorotatory (-) and dexorotatory (+).
Achiral Diastereomers (meso-Compounds)
Exercise \(\PageIndex{1}\)
Beside meso, there are also other types of molecules: enantiomer, diastereomer, and identical. Determine if the following molecules are meso.
- Answer
-
A C, D, E are meso compounds.
Contributors and Attributions
- Duy Dang
- Gamini Gunawardena from the OChemPal site (Utah Valley University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)

