14.21: Two-Dimensional NMR Spectroscopy

Nuclear Magnetic Resonance (NMR) interpretation plays a pivotal role in molecular identifications. As interpreting NMR spectra, the structure of an unknown compound, as well as known structures, can be assigned by several factors such as chemical shift, spin multiplicity, coupling constants, and integration. This Module focuses on the most important ¹H and ¹³C NMR spectra to find out structure even though there are various kinds of NMR spectra such as ¹⁴N, ¹⁹F, and ³¹P. NMR spectrum shows that x- axis is chemical shift in ppm. It also contains integral areas, splitting pattern, and coupling constant.

Strategy for Solving Structure

Here is the general strategy for solving structure with NMR:

1. Molecular formula is determined by chemical analysis such as elementary analysis
2. Double-bond equivalent (also known as Degree of Unsaturation) is calculated by a simple equation to estimate the number of the multiple bonds and rings. It assumes that oxygen (O) and sulfur (S) are ignored and halogen (Cl, Br) and nitrogen is replaced by CH. The resulting empirical formula is C_aH_b

3. Structure fragmentation is determined by chemical shift, spin multiplicity, integral (peak area), and coupling constants (\(^1J\), \(^2J\))
4. Molecular skeleton is built up using 2-dimensional NMR spectroscopy.
5. Relative configuration is predicted by coupling constant (³J).

¹H NMR

Chemical Shift

Chemical shift is associated with the Larmor frequency of a nuclear spin to its chemical environment. Tetramethylsilane (TMS, \(\ce{(CH3)4Si}\)) is generally used as an internal standard to determine chemical shift of compounds: δ_TMS=0 ppm. In other words, frequencies for chemicals are measured for a ¹H or ¹³C nucleus of a sample from the ¹H or ¹³C resonance of TMS. It is important to understand trend of chemical shift in terms of NMR interpretation. The proton NMR chemical shift is affect by nearness to electronegative atoms (O, N, halogen.) and unsaturated groups (C=C,C=O, aromatic). Electronegative groups move to the down field (left; increase in ppm). Unsaturated groups shift to downfield (left) when affecting nucleus is in the plane of the unsaturation, but reverse shift takes place in the regions above and below this plane. ¹H chemical shift play a role in identifying many functional groups. Figure \(\PageIndex{1}\). indicates important example to figure out the functional groups.

Figure \(\PageIndex{1}\): 1H chemical shift ranges for organic compound

Chemical equivalence

Protons with Chemical equivalence has the same chemical shift due to symmetry within molecule (\(CH_3COCH_3\)) or fast rotation around single bond (-CH₃; methyl groups).

Spin-Spin Splitting

Spin-Spin splitting means that an absorbing peak is split by more than one “neighbor” proton. Splitting signals are separated to J Hz, where is called the coupling constant. The spitting is a very essential part to obtain exact information about the number of the neighboring protons. The maximum of distance for splitting is three bonds. Chemical equivalent protons do not result in spin-spin splitting. When a proton splits, the proton’s chemical shift is determined in the center of the splitting lines.

Spin Multiplicity (Splitting pattern)

Spin Multiplicity plays a role in determining the number of neighboring protons. Here is a multiplicity rules: In case of \(A_mB_n\) system, the multiplicity rule is that Nuclei of \(B\) element produce a splitting the \(A\) signal into \(nB+1\) lines. The general formula which applies to all nuclei is \(2_nI+1\), where \(I\) is the spin quantum number of the coupled element. The relative intensities of the each lines are given by the coefficients of the Pascal’s triangle (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): Pascal's triangle

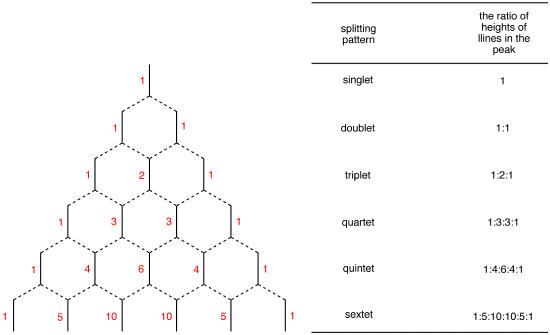
First-order splitting pattern

The chemical shift difference in Hertz between coupled protons in Hertz is much larger than the \(J\) coupling constant:

\[ \dfrac{\Delta \nu }{J} \ge 8\]

Where \(\Delta \nu\) is the difference of chemical shift. In other word, the proton is only coupled to other protons that are far away in chemical shift. The spectrum is called first-order spectrum. The splitting pattern depends on the magnetic field. The second-order splitting at the lower field can be resolved into first-order splitting pattern at the high field. The first-order splitting pattern is allowed to multiplicity rule (N+1) and Pascal’s triangle to determine splitting pattern and intensity distribution.

Example \(\PageIndex{1}\)

The note is that structure system is A₃M₂X₂. H_a and H_x has the triplet pattern by Hm because of N+1 rule. The signal of Hm is split into six peaks by H_x and H_a (Figure3) The First order pattern easily is predicted due to separation with equal splitting pattern.

Figure \(\PageIndex{3}\): An example of splitting pattern

High-order splitting pattern

High-order splitting pattern takes place when chemical shift difference in Hertz is much less or the same that order of magnitude as the j coupling.

\[\frac{\Delta v}{J} \leq 10\]

The second order pattern is observed as leaning of a classical pattern: the inner peaks are taller and the outer peaks are shorter in case of AB system (Figure \(\PageIndex{4}\)). This is called the roof effect.

Figure \(\PageIndex{4}\): a) first-order pattern and b) second-order pattern of AB system

Here is other system as an example: A₂B₂ (Figure \(\PageIndex{5}\)). The two triplet incline toward each other. Outer lines of the triplet are less than 1 in relative area and the inner lines are more than 1. The center lines have relative area 2.

Figure \(\PageIndex{5}\): a) first-order pattern and b) second-order pattern of A₂B₂ system

Coupling constant (J Value)

Coupling constant is the strength of the spin-spin splitting interaction and the distance between the split lines. The value of distance is equal or different depending on the coupled nuclei. The coupling constants reflect the bonding environments of the coupled nuclei. Coupling constant is classified by the number of bonds:

Geminal proton-proton coupling (²J_HH)

Germinal coupling generates through two bonds (Figure \(\PageIndex{6}\)). Two proton having geminal coupling are not chemically equivalent. This coupling ranges from -20 to 40 Hz. ²J_HHdepends on hybridization of carbon atom and the bond angle and the substituent such as electronegative atoms. When S-character is increased, Geminal coupling constant is increased: ²J_sp1>²J_sp2>²J_sp3 The bond angle(HCH) gives rise to change ²J_HH value and depend on the strain of the ring in the cyclic systems. Geminal coupling constant determines ring size. When bond angle is decreased, ring size is decreased so that geminal coupling constant is more positive. If a atom is replace to an electronegative atom, Geminal coupling constant move to positive value.

Figure \(\PageIndex{6}\): Geminal coupling

Vicinal proton-proton coupling (³J_HH)

Vicinal coupling occurs though three bonds (Figure \(\PageIndex{7}\).). The Vicinal coupling is the most useful information of dihedral angle, leading to stereochemistry and conformation of molecules. Vicinal coupling constant always has the positive value and is affected by the dihedral angle (?;HCCH), the valence angle (?; HCC), the bond length of carbon-carbon, and the effects of electronegative atoms. Vicinal coupling constant depending on the dihedral angle (Figure \(\PageIndex{8}\)) is given by the Karplus equation.

\[^3 J=7.0-0.5 \cos \phi+4.5 \cos ^{2} \phi\]

When ? is the 90^o, vicinal coupling constant is zero. In addition, vicinal coupling constant ranges from 8 to 10 Hz at the and ?=180^o, where ?=0^o and ?=180^o means that the coupled protons have cis and trans configuration, respectively.

Figure \(\PageIndex{7}\): Vicinal coupling

The valence angle(?;Figure \(\PageIndex{8}\)) also causes change of ³J_HH value. Valence angle is related with ring size. Typically, when the valence angle decreases, the coupling constant reduces. The distance between the carbons atoms gives influences to vicinal coupling constant

Figure \(\PageIndex{8}\): a) Dihedral angle and b) valence angle

The coupling constant increases with the decrease of bond length. Electronegative atoms affect vicinal coupling constants so that electronegative atoms decrease the vicinal coupling constants.

Integral

Integral is referred to integrated peak area of 1H signals. The intensity is directly proportionally to the number of hydrogen.

¹³C NMR

Chemical Shift

Figure \(\PageIndex{9}\) shows typical ¹³C chemical shift regions of the major chemical class.

Figure \(\PageIndex{9}\): ¹³C Chemical shift range for organic compound

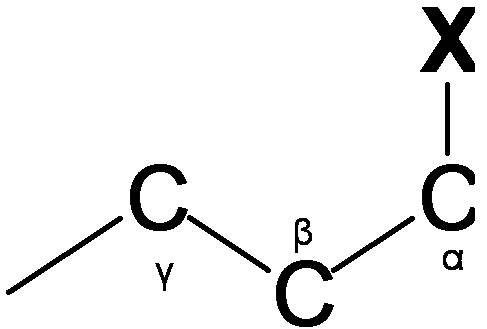
Spin-Spin splitting

Comparing the ¹H NMR, there is a big difference thing in the ¹³C NMR. The ¹³C- ¹³ C spin-spin splitting rarely exit between adjacent carbons because ¹³C is naturally lower abundant (1.1%)

• ¹³C-¹H Spin coupling: ¹³C-¹H Spin coupling provides useful information about the number of protons attached a carbon atom. In case of one bond coupling (¹J_CH), -CH, -CH₂, and CH₃ have respectively doublet, triplet, quartets for the ¹³C resonances in the spectrum. However, ¹³C-¹H Spin coupling has an disadvantage for ¹³C spectrum interpretation. ¹³C-¹H Spin coupling is hard to analyze and reveal structure due to a forest of overlapping peaks that result from 100% abundance of ¹H.
• Decoupling: Decoupling is the process of removing ¹³C-¹H coupling interaction to simplify a spectrum and identify which pair of nuclei is involved in the J coupling. The decoupling ¹³C spectra shows only one peak(singlet) for each unique carbon in the molecule(Figure \(\PageIndex{10}\).). Decoupling is performed by irradiating at the frequency of one proton with continuous low-power RF.

Figure \(\PageIndex{10}\). Decoupling in the ¹³C NMR

• Distortionless enhancement by polarization transfer (DEPT): DEPT is used for distinguishing between a CH₃ group, a CH₂ group, and a CH group. The proton pulse is set at 45^o, 90^o, or 135^o in the three separate experiments. The different pulses depend on the number of protons attached to a carbon atom. Figure \(\PageIndex{11}\). is an example about DEPT spectrum.

Figure \(\PageIndex{11}\). DEPT spectrum of n-isobutlybutrate

2-dimensional NMR spectroscopy (COSY)

COSY stands for COrrelation SpectroscopY. COSY spectrum is more useful information about what is being correlated.

¹H-¹H COSY (COrrelation SpectroscopY)

¹H-¹H COSY is used for clearly indicate correlation with coupled protons. A point of entry into a COSY spectrum is one of the keys to predict information from it successfully. Relation of Coupling protons is determined by cross peaks(correlation peaks) and in the COSY spectrum. In other words, Diagonal peaks by lines ar e coupled to each other. Figure \(\PageIndex{12}\) indicates that there are correlation peaks between proton H₁ and H₂ as well as between H₂ and H₄. This means the H₂ coupled to H₁ and H₄.

Figure \(\PageIndex{12}\). ¹H-¹H COSY spectrum

¹H-¹³C COSY (HETCOR)

¹H-¹³C COSY is the heteronuclear correlation spectroscopy. The HETCOR spectrum is correlated ¹³C nuclei with directly attached protons. ¹H-¹³C coupling is one bond. The cross peaks mean correlation between a proton and a carbon (Figure \(\PageIndex{13}\)). If a line does not have cross peak, this means that this carbon atoms has no attached proton (e.g. a quaternary carbon atom)

Figure \(\PageIndex{13}\). ¹H-¹³C COSY spectrum

References

1. Balc*, M., Basic p1 sH- and p13 sC-NMR spectroscopy. 1st ed.; Elsevier: Amsterdam ; Boston, 2005; p xii, 427.
2. Breitmaier, E., Structure elucidation by NMR in organic chemistry : a practical guide. 3rd rev. ed.; Wiley: Chichester, West Sussex, England, 2002; p xii, 258.
3. Jacobsen, N. E., NMR spectroscopy explained : simplified theory, applications and examples for organic chemistry and structural biology. Wiley-Interscience: Hoboken, N.J., 2007; p xv, 668.
4. Silverstein, R. M.; Webster, F. X., Spectrometric identification of organic compounds. 6th ed.; Wiley: New York, 1998; p xiv, 482.

Outside Links

• NMRShiftDB: a Free web database for NMR data : nmrshiftdb.chemie.uni-mainz.de/nmrshiftdb
• NMR database from ACD/LAbs : www.acdlabs.com/products/spec_lab/exp_spectra/spec_libraries/aldrich.html
• NMR database from John Crerar Library : http://crerar.typepad.com/crerar_lib...h_ir_nmr_.html

Problems

Draw the 1H NMR spectrum for 2-Hydroxypropane in CDCl3. Assume sufficient resolution to provide a first-order spectrum and ignore vicinal proton-proton coupling(3JHH)

Solution

1) the structure of 2-hydoroxyporpane is drawn

Figure out which protons are chemically equivalent, i.e., two methyl (-CH₃) groups are chemical equivalent.

Figure1): chemical shift of methyl groups (H_a) : 1-2 ppm (?H_a=1.1 ppm); chemical shift of -CH- groups (H_b) moves to downfield due to effect on aldehyde groups:2-3ppm ( ?H_b=2.4 ppm); chemical shift of aldehyde groups (H_c):9-10 ppm (?H_c=9.6 ppm)

4) Splitting pattern is determined by (N+1) rule: Ha is split into two peaks by H_b(#of proton=1). H_b has the septet pattern by H_a (#of proton=6). H_c has one peak.(Note that H_c has doublet pattern by H_b due to vicinal proton-proton coupling.)

Contributors and Attributions

• You Jin Seo