15.9: What Is the Basis of Hückel’s Rule?
- Page ID
- 30656
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aromaticity
Molecular orbital theory is especially helpful in explaining the unique properties of a class of compounds called aromatics. Benzene, a common organic solvent, is the simplest example of an aromatic compound.
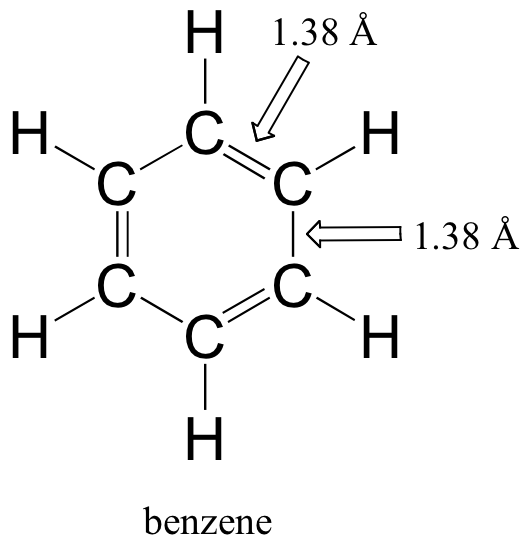
Although it is most often drawn with three double bonds and three single bonds, it is known that all of the carbon-carbon bonds in benzene are exactly the same length - 1.38 Å. This is shorter than a typical carbon-carbon single bond (about 1.54 Å), and slightly longer than a typical carbon-carbon double bond (about 1.34 Å).
In addition, the π bonds in benzene are significantly less reactive than isolated or conjugated π bonds in most alkenes. To illustrate this unique stability, we will make use of the idea of ‘heat of hydrogenation’. The carbon-carbon double bond in an alkene can be converted to a single bond through a process called ‘catalytic hydrogenation’ –essentially adding a molecule of H2 to the double bond.
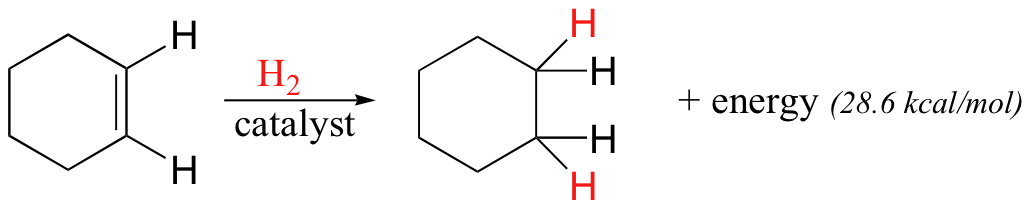
We will learn more about how this process occurs, both in the laboratory and in living cells, later in the text (section 16.5). For now, what is important to understand is that the hydrogenation process is exothermic: the alkane is lower in energy than the alkene, so hydrogenating the double bond results in the release of energy in the form of heat. Converting one mole of cyclohexene to cyclohexane, for example, releases 28.6 kilocalories. If the benzene molecule is considered to be a six-membered ring with three isolated double bonds, the heat of hydrogenation should theoretically be three times this value, or 85.8 kcal/mol. The actual heat of hydrogenation of benzene, however, is only 49.8 kcal/mol, or 36 kcal/mol less than what we would expect if using the isolated double bond model. Something about the structure of benzene makes these π bonds especially stable. This ‘something’ has a name: it is called ‘aromaticity’.
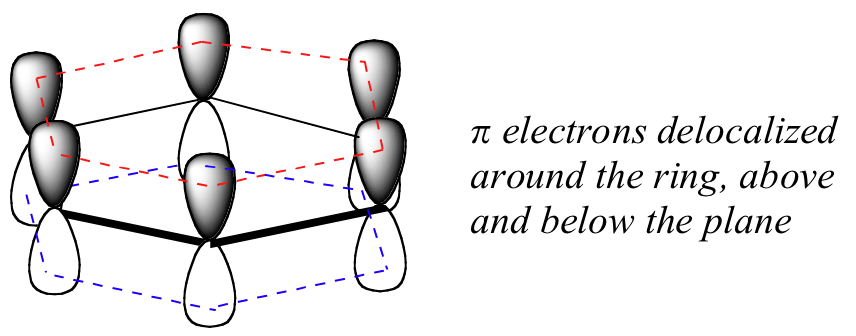
What exactly is this ‘aromatic’ property that makes the pbonds in benzene so much less reactive than those in alkenes? In a large part, the answer to this question lies in the fact that benzene is a cyclic molecule in which all of the ring atoms are sp2-hybridized. This allows the π electrons to be delocalized in molecular orbitals that extend all the way around the ring, above and below the plane of the ring. For this to happen, of course, the ring must be planar – otherwise the 2pz orbitals couldn’t overlap properly. Benzene is indeed known to be a flat molecule.
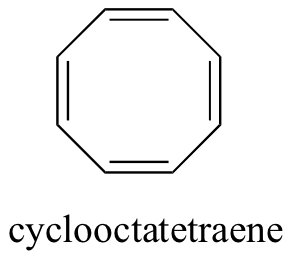
Do all cyclic molecules with alternating single and double bonds have this same aromatic stability? Quite simply, the answer is ‘no’. The eight-membered cyclooctatetraene ring shown below is not flat, and its π bonds are much more reactive than those of benzene.
Clearly it takes something more to be aromatic, and this can best be explained with molecular orbital theory. Let’s look at an energy diagram for the molecular orbitals containing the π electrons in benzene.
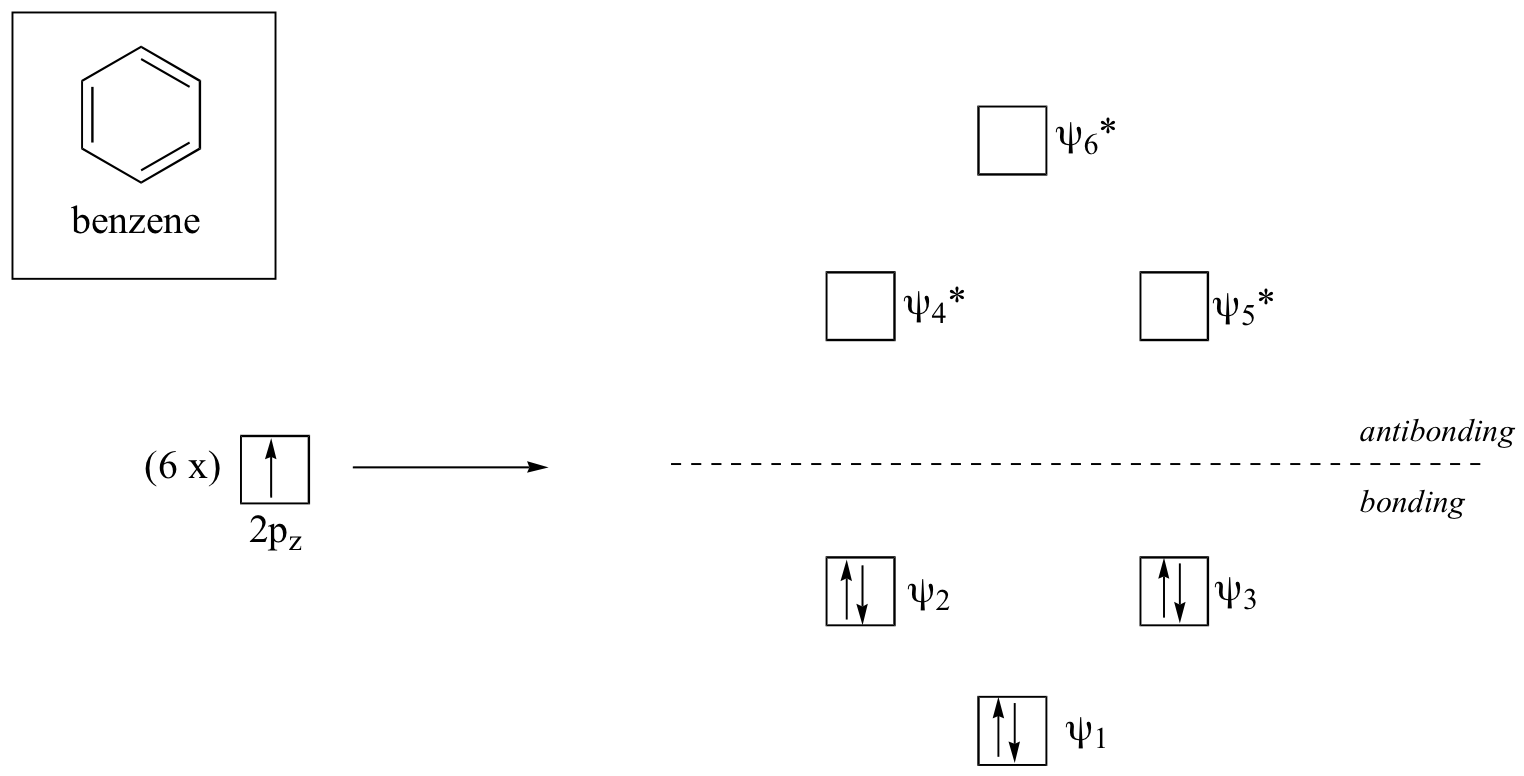
Quantum mechanical calculations conclude that the six molecular orbitals in benzene, formed from six atomic 2pz orbitals, occupy four separate energy levels. Ψ1 and Ψ6* have unique energy levels, while the Ψ2- Ψ3 and Ψ4*-Ψ5* pairs are degenerate (more than one orbital at the same energy level). When we use the aufbau principle to fill up these orbitals with the six π electrons in benzene, we see that the bonding orbitals are completely filled, and the antibonding orbitals are empty. This gives us a good clue to the source of the special stability of benzene: a full set of bonding MO’s is similar in many ways to the ‘full shell’ of electrons possessed by the very stable noble gases like helium, neon, and argon.
Now, let’s do the same thing for cyclooctatetraene, which we have already learned is not aromatic.

The result of molecular orbital calculations tells us that the lowest and highest energy MOs (Ψ1 and Ψ8*) have unique energy levels, while the other six come in degenerate pairs. Notice that y4and y5are at the same energy level as the isolated 2pz atomic orbitals: these are therefore neither bonding nor antibonding, rather they are referred to as nonbonding MOs. Filling up the MOs with the eight π electrons in the molecule, we find that the last two electrons are unpaired and fall into the two degenerate nonbonding orbitals. Because we don't have a perfect filled shell of bonding MOs, our molecule is not aromatic. As a consequence, each of the double bonds in cyclooctatetraene acts more like an isolated double bond.
Here, then, are the conditions that must be satisfied for a molecule to be considered aromatic:
- It must have a cyclic structure.
- The ring must be planar.
- Each atom in the ring must be sp2-hybridized, so that π electrons can be delocalized around the ring.
- The number of π electrons in the ring must be such that, in the ground state of the molecule, all bonding MOs are completely filled, and all nonbonding and antibonding MOs are completely empty.
It turns out that, in order to satisfy condition #4, the ring must contain a specific number of π electrons. The set of possible numbers is quite easy to remember - the rule is simply 4n+2, where n is any positive integer (this is known as the Hückel rule, named after Erich Hückel, a German scientist who studied aromatic compounds in the 1930’s). Thus, if n = 0, the first Hückel number is (4 x 0) + 2, or 2. If n = 1, the Hückel number is (4 x 1) + 2, or 6 (the Hückel number for benzene). The series continues with 10, 14, 18, 22, and so on. Cyclooctatetraene has eight π electrons, which is not a Hückel number. Because 6 is such a common Hückel number, chemists often use the term 'aromatic sextet'.
Benzene is best visualized as a planar ring made up of carbon-carbon sbonds, with two ‘donut-like’ rings of fully delocalized π electron density above and below the plane of the ring (the fact that there is a ring of π electron density on both sides of the molecule stems from the fact that the overlapping p orbitals have two lobes, and the electron density is located in both). This general picture is valid not just for benzene but for all other aromatic structures as well.
Let’s look at some different aromatic compounds other than benzene. Pyridine and pyrimidine both fulfill all of the criteria for aromaticity.
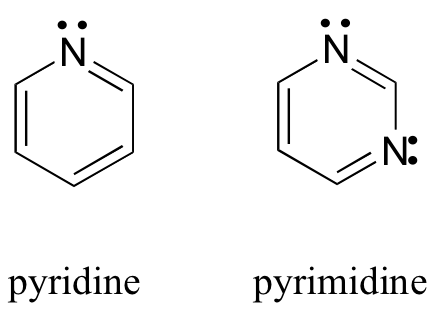
In both of these molecules, the nitrogen atoms are sp2 hybridized, with the lone pair occupying an sp2 orbital and therefore not counted among the aromatic sextet. The Hückel number for both pyridine and pyrimidine is six.
Rings do not necessarily need to be 6-membered in order to have six π electrons. Pyrrole and imidizole, for example, are both aromatic 5-membered rings with six π electrons.
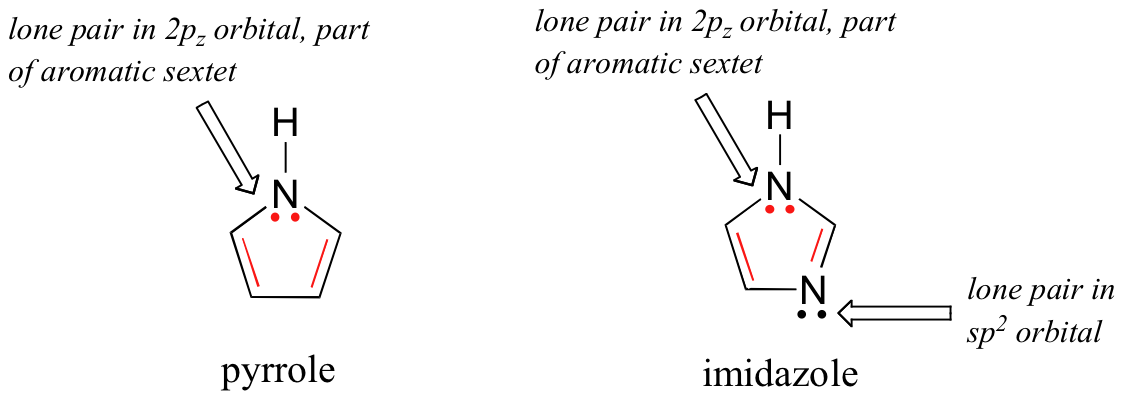
The nitrogen atoms in both of these molecules are sp2-hybridized (as they must be for the rings to be aromatic). In pyrrole, the lone pair can be thought of as occupying a 2pz orbital, and thus both of these electrons contribute to the aromatic π system. In imidazole, one lone pair occupies a 2pz orbital and is part of the aromatic sextet, while the second occupies one of the sp2 orbitals and is not part of the sextet.
Molecules with more then one ring can also fulfill the Hückel criteria, and often have many of the same properties as monocyclic aromatic compounds, including a planar structure. Indole (a functional group in the amino acid tryptophan) and purine (a functional group in guanine and adenine DNA/RNA bases) both have a total of ten π electrons delocalized around two rings.
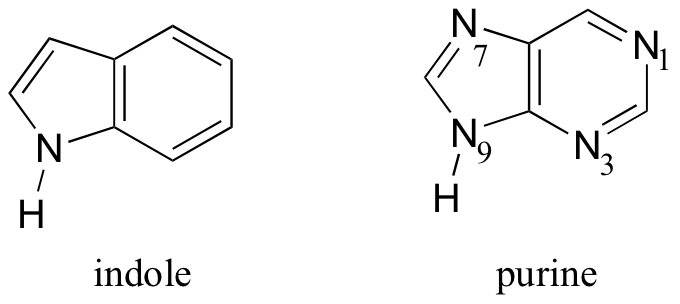
The nitrogen in indole and the N9 nitrogen in purine both contribute a pair of electrons to the π system. The N1, N3, and N7 nitrogens of purine, in contrast, hold their lone pair in sp2 orbitals, outside of the aromatic system.
| Example |
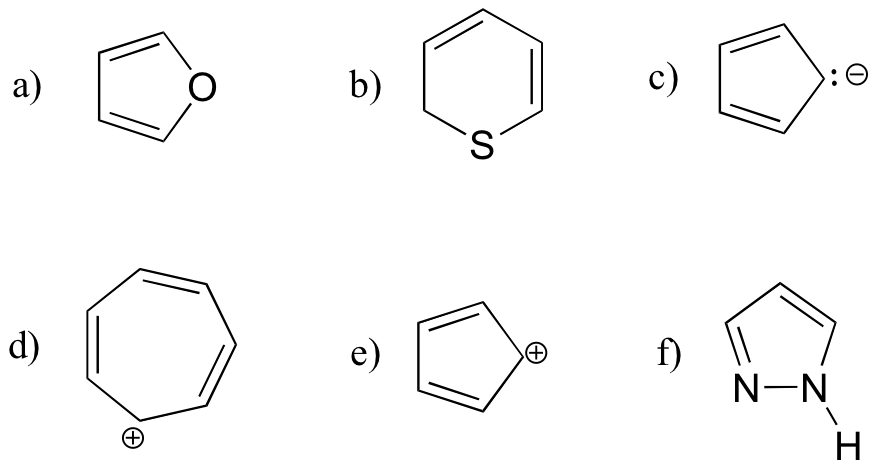
Exercise 2.2: Are the following molecules likely to be aromatic? Explain, using Huckel’s criteria. and orbital drawings. Hint: Ions can also be aromatic!
Up to now we have been talking about molecules in which the entire structure makes up an aromatic system. However, in organic chemistry we will more often encounter examples of molecules which have both aromatic and nonaromatic parts. Toluene, a common organic solvent (which is much safer to use than benzene) is simply a benzene ring with a methyl substituent. Benzyaldehyde is benzene with an aldehyde substituent, and phenol is benzene with a hydroxyl substituent.
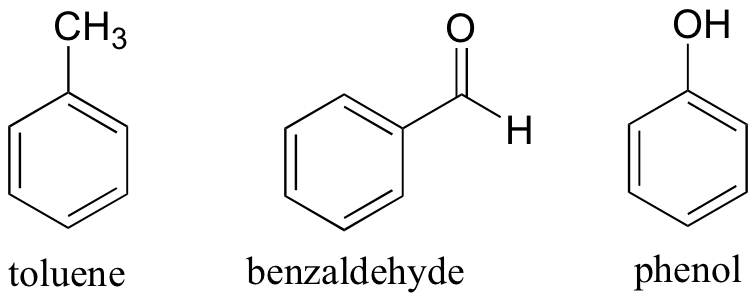
In these ‘substituted benzene’ compounds, the entire molecule is not aromatic, just the benzene ring part.
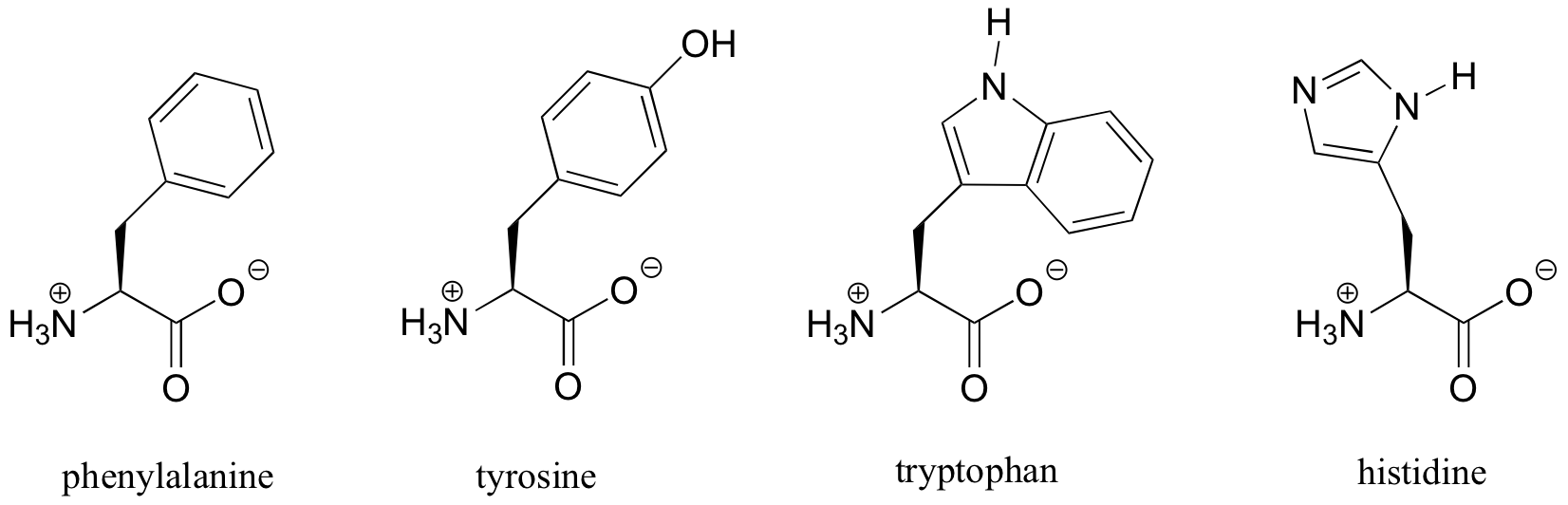
When a benzene ring is part of a larger molecule, it is called a ‘phenyl’ group. The amino acid phenylalanine, for example, contains a phenyl group. The amino acids tyrosine, tryptophan, and histidine contain phenol, indole, and imidazole groups, respectively.
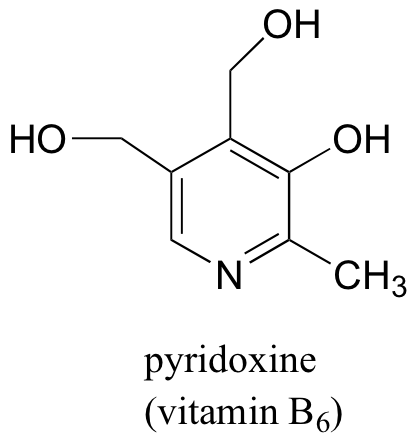
Pyridoxine, commonly known as vitamin B6, is a substituted pyridine.
The DNA and RNA bases are based on pyrimidine (cytosine, thymine, and uracil) and purine (adenine and guanine).
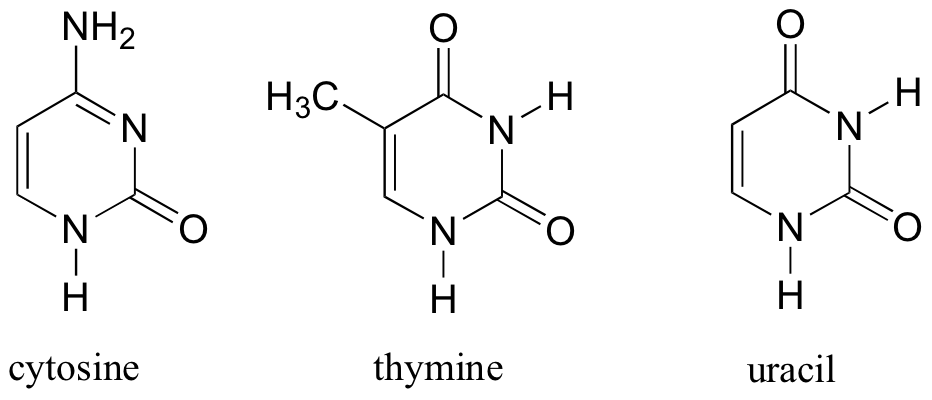
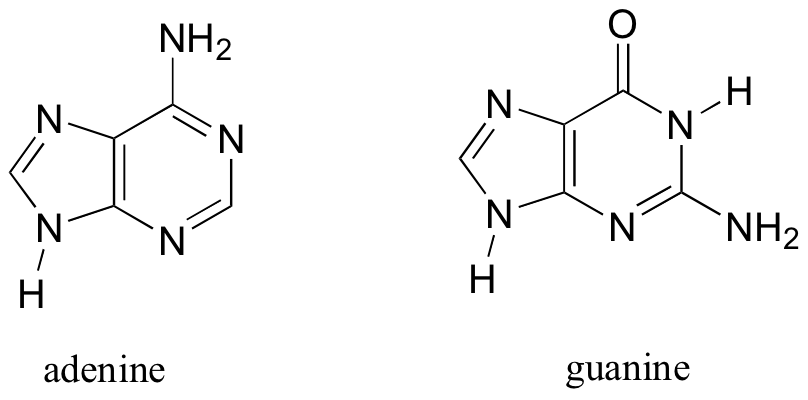
The flat, aromatic structure of these bases plays a critical role in the overall structure and function of DNA and RNA.
Contributors
- Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

