13.20: The Visible Spectrum and Color
- Page ID
- 16354
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page explains what happens when organic compounds absorb UV or visible light, and why the wavelength of light absorbed varies from compound to compound.
What happens when light is absorbed by molecules?
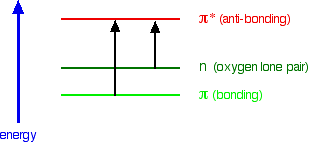
When we were talking about the various sorts of orbitals present in organic compounds on the introductory page (see above), you will have come across this diagram showing their relative energies:

Remember that the diagram isn't intended to be to scale - it just shows the relative placing of the different orbitals. When light passes through the compound, energy from the light is used to promote an electron from a bonding or non-bonding orbital into one of the empty anti-bonding orbitals. The possible electron jumps that light might cause are:

In each possible case, an electron is excited from a full orbital into an empty anti-bonding orbital. Each jump takes energy from the light, and a big jump obviously needs more energy than a small one. Each wavelength of light has a particular energy associated with it. If that particular amount of energy is just right for making one of these energy jumps, then that wavelength will be absorbed - its energy will have been used in promoting an electron.
We need to work out what the relationship is between the energy gap and the wavelength absorbed. Does, for example, a bigger energy gap mean that light of a lower wavelength will be absorbed - or what? It is easier to start with the relationship between the frequency of light absorbed and its energy:
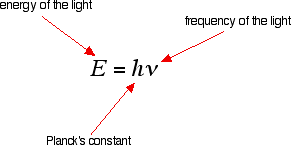
You can see that if you want a high energy jump, you will have to absorb light of a higher frequency. The greater the frequency, the greater the energy. That's easy - but unfortunately UV-visible absorption spectra are always given using wavelengths of light rather than frequency. That means that you need to know the relationship between wavelength and frequency.
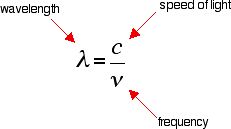
You can see from this that the higher the frequency is, the lower the wavelength is. So, if you have a bigger energy jump, you will absorb light with a higher frequency - which is the same as saying that you will absorb light with a lower wavelength.
Important summary: The larger the energy jump, the lower the wavelength of the light absorbed.
Some jumps are more important than others for absorption spectrometry
An absorption spectrometer works in a range from about 200 nm (in the near ultra-violet) to about 800 nm (in the very near infra-red). Only a limited number of the possible electron jumps absorb light in that region. Look again at the possible jumps. This time, the important jumps are shown in black, and a less important one in grey. The grey dotted arrows show jumps which absorb light outside the region of the spectrum we are working in.
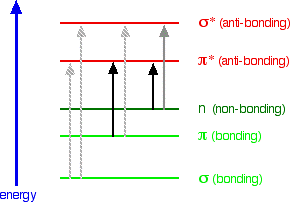
Remember that bigger jumps need more energy and so absorb light with a shorter wavelength. The jumps shown with grey dotted arrows absorb UV light of wavelength less that 200 nm. The important jumps are:
- from pi bonding orbitals to pi anti-bonding orbitals;
- from non-bonding orbitals to pi anti-bonding orbitals;
- from non-bonding orbitals to sigma anti-bonding orbitals.
That means that in order to absorb light in the region from 200 - 800 nm (which is where the spectra are measured), the molecule must contain either pi bonds or atoms with non-bonding orbitals. Remember that a non-bonding orbital is a lone pair on, say, oxygen, nitrogen or a halogen.
Groups in a molecule which absorb light are known as chromophores.
What does an absorption spectrum look like
The diagram below shows a simple UV-visible absorption spectrum for buta-1,3-diene - a molecule we will talk more about later. Absorbance (on the vertical axis) is just a measure of the amount of light absorbed. The higher the value, the more of a particular wavelength is being absorbed.
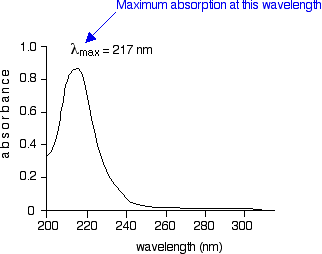
You will see that absorption peaks at a value of 217 nm. This is in the ultra-violet and so there would be no visible sign of any light being absorbed - buta-1,3-diene is colorless. You read the symbol on the graph as "lambda-max". In buta-1,3-diene, CH2=CH-CH=CH2, there are no non-bonding electrons. That means that the only electron jumps taking place (within the range that the spectrometer can measure) are from pi bonding to pi anti-bonding orbitals.
A chromophore producing two peaks
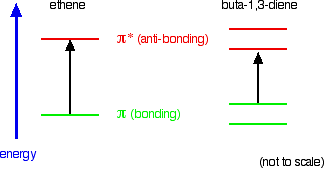
A chromophore such as the carbon-oxygen double bond in ethanal, for example, obviously has pi electrons as a part of the double bond, but also has lone pairs on the oxygen atom. That means that both of the important absorptions from the last energy diagram are possible. You can get an electron excited from a pi bonding to a pi anti-bonding orbital, or you can get one excited from an oxygen lone pair (a non-bonding orbital) into a pi anti-bonding orbital.
The non-bonding orbital has a higher energy than a pi bonding orbital. That means that the jump from an oxygen lone pair into a pi anti-bonding orbital needs less energy. That means it absorbs light of a lower frequency and therefore a higher wavelength. Ethanal can therefore absorb light of two different wavelengths:
- the pi bonding to pi anti-bonding absorption peaks at 180 nm;
- the non-bonding to pi anti-bonding absorption peaks at 290 nm.
Both of these absorptions are in the ultra-violet, but most spectrometers won't pick up the one at 180 nm because they work in the range from 200 - 800 nm.
The importance of conjugation and delocalisation
Consider these three molecules:
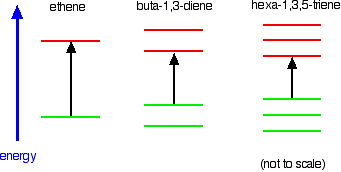
Ethene contains a simple isolated carbon-carbon double bond, but the other two have conjugated double bonds. In these cases, there is delocalization of the pi bonding orbitals over the whole molecule. Now look at the wavelengths of the light which each of these molecules absorbs.
| molecule | wavelength of maximum absorption (nm) |
|---|---|
| ethene | 171 |
| buta-1,3-diene | 217 |
| hexa-1,3,5-triene | 258 |
All of the molecules give similar UV-visible absorption spectra - the only difference being that the absorptions move to longer and longer wavelengths as the amount of delocalization in the molecule increases.
Why is this? You can actually work out what must be happening.
- The maximum absorption is moving to longer wavelengths as the amount of delocalization increases.
- Therefore maximum absorption is moving to shorter frequencies as the amount of delocalization increases.
- Therefore absorption needs less energy as the amount of delocalization increases.
- Therefore there must be less energy gap between the bonding and anti-bonding orbitals as the amount of delocalization increases.
. . . and that's what is happening.
Compare ethene with buta-1,3-diene. In ethene, there is one pi bonding orbital and one pi anti-bonding orbital. In buta-1,3-diene, there are two pi bonding orbitals and two pi anti-bonding orbitals. This is all discussed in detail on the introductory page that you should have read.
The highest occupied molecular orbital is often referred to as the HOMO - in these cases, it is a pi bonding orbital. The lowest unoccupied molecular orbital (the LUMO) is a pi anti-bonding orbital. Notice that the gap between these has fallen. It takes less energy to excite an electron in the buta-1,3-diene case than with ethene.
In the hexa-1,3,5-triene case, it is less still.
If you extend this to compounds with really massive delocalisation, the wavelength absorbed will eventually be high enough to be in the visible region of the spectrum, and the compound will then be seen as colored. A good example of this is the orange plant pigment, beta-carotene - present in carrots, for example.
Why is beta-carotene orange?
Beta-carotene has the sort of delocalization that we've just been looking at, but on a much greater scale with 11 carbon-carbon double bonds conjugated together. The diagram shows the structure of beta-carotene with the alternating double and single bonds shown in red.
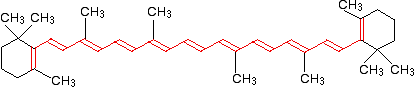
The more delocalization there is, the smaller the gap between the highest energy pi bonding orbital and the lowest energy pi anti-bonding orbital. To promote an electron therefore takes less energy in beta-carotene than in the cases we've looked at so far - because the gap between the levels is less.
Remember that less energy means a lower frequency of light gets absorbed - and that's equivalent to a longer wavelength. Beta-carotene absorbs throughout the ultra-violet region into the violet - but particularly strongly in the visible region between about 400 and 500 nm with a peak about 470 nm. If you have read the page in this section about electromagnetic radiation, you might remember that the wavelengths associated with the various colors are approximately:
| color region | wavelength (nm) |
|---|---|
| violet | 380 - 435 |
| blue | 435 - 500 |
| cyan | 500 - 520 |
| green | 520 - 565 |
| yellow | 565 - 590 |
| orange | 590 - 625 |
| red | 625 - 740 |
So if the absorption is strongest in the violet to cyan region, what color will you actually see? It is tempting to think that you can work it out from the colors that are left - and in this particular case, you wouldn't be far wrong. Unfortunately, it isn't as simple as that!
Sometimes what you actually see is quite unexpected. Mixing different wavelengths of light doesn't give you the same result as mixing paints or other pigments. You can, however, sometimes get some estimate of the color you would see using the idea of complementary colors.
Complementary colors
If you arrange some colors in a circle, you get a "color wheel". The diagram shows one possible version of this. An internet search will throw up many different versions!
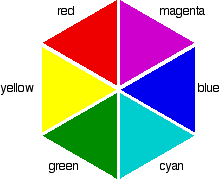
colors directly opposite each other on the color wheel are said to be complementary colors. Blue and yellow are complementary colors; red and cyan are complementary; and so are green and magenta. Mixing together two complementary colors of light will give you white light.
What this all means is that if a particular color is absorbed from white light, what your eye detects by mixing up all the other wavelengths of light is its complementary color. In the beta-carotene case, the situation is more confused because you are absorbing such a range of wavelengths. However, if you think of the peak absorption running from the blue into the cyan, it would be reasonable to think of the color you would see as being opposite that where yellow runs into red - in other words, orange.
Applying this to the color changes of two indicators
Phenolphthalein
You have probably used phenolphthalein as an acid-base indicator, and will know that it is colorless in acidic conditions and magenta (bright pink) in an alkaline solution. How is this color change related to changes in the molecule? The structures of the two differently colored forms are:
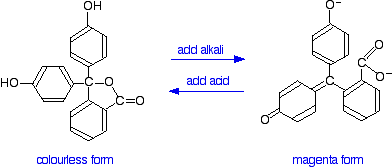
Both of these absorb light in the ultra-violet, but the one on the right also absorbs in the visible with a peak at 553 nm. The molecule in acid solution is colorless because our eyes can't detect the fact that some light is being absorbed in the ultra-violet. However, our eyes do detect the absorption at 553 nm produced by the form in alkaline solution.
553 nm is in the green region of the spectrum. If you look back at the color wheel, you will find that the complementary color of green is magenta - and that's the color you see.
So why does the color change as the structure changes? What we have is a shift to absorption at a higher wavelength in alkaline solution. As we've already seen, a shift to higher wavelength is associated with a greater degree of delocalisation.
Here is a modified diagram of the structure of the form in acidic solution - the colorless form. The extent of the delocalization is shown in red.
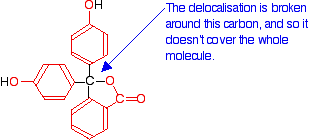
Notice that there is delocalization over each of the three rings - extending out over the carbon-oxygen double bond, and to the various oxygen atoms because of their lone pairs.
But the delocalization doesn't extend over the whole molecule. The carbon atom in the centre with its four single bonds prevents the three delocalized regions interacting with each other.
Now compare that with the magenta form:
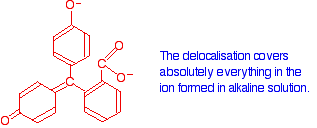
The rearrangement now lets the delocalization extend over the entire ion. This greater delocalization lowers the energy gap between the highest occupied molecular orbital and the lowest unoccupied pi anti-bonding orbital. It needs less energy to make the jump and so a longer wavelength of light is absorbed.
Increasing the amount of delocalization shifts the absorption peak to a higher wavelength.
Methyl orange
You will know that methyl orange is yellow in alkaline solutions and red in acidic ones. The structure in alkaline solution is:
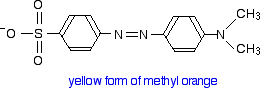
In acid solution, a hydrogen ion is (perhaps unexpectedly) picked up on one of the nitrogens in the nitrogen-nitrogen double bond.
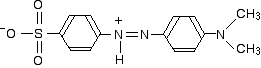
This now gets a lot more complicated! The positive charge on the nitrogen is delocalized (spread around over the structure) - especially out towards the right-hand end of the molecule as we've written it. The normally drawn structure for the red form of methyl orange is . . .
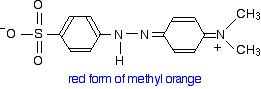
But this can be seriously misleading as regards the amount of delocalization in the structure for reasons discussed below (after the red warning box) if you are interested.
Which is the more delocalized structure?
Let's work backwards from the absorption spectra to see if that helps. The yellow form has an absorption peak at about 440 nm. That's in the blue region of the spectrum, and the complementary color of blue is yellow. That's exactly what you would expect. The red form has an absorption peak at about 520 nm. That's at the edge of the cyan region of the spectrum, and the complementary color of cyan is red. Again, there's nothing unexpected here.
Notice that the change from the yellow form to the red form has produced an increase in the wavelength absorbed. An increase in wavelength suggests an increase in delocalisation. That means that there must be more delocalization in the red form than in the yellow one. Here again is the structure of the yellow form:

delocalization will extend over most of the structure - out as far as the lone pair on the right-hand nitrogen atom.
If you use the normally written structure for the red form, the delocalization seems to be broken in the middle - the pattern of alternating single and double bonds seems to be lost.

But that is to misunderstand what this last structure represents.
Canonical forms
If you draw the two possible Kekulé structures for benzene, you will know that the real structure of benzene isn't like either of them. The real structure is somewhere between the two - all the bonds are identical and somewhere between single and double in character. That's because of the delocalization in benzene.
The two structures are known as canonical forms, and they can each be thought of as adding some knowledge to the real structure. For example, the bond drawn at the top right of the molecule is neither truly single or double, but somewhere in between. Similarly with all the other bonds.
The two structures we've previously drawn for the red form of methyl orange are also canonical forms - two out of lots of forms that could be drawn for this structure. We could represent the delocalized structure by:
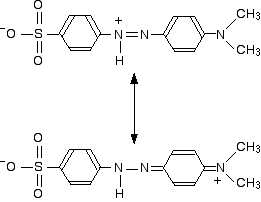
These two forms can be thought of as the result of electron movements in the structure, and curly arrows are often used to show how one structure can lead to the other.
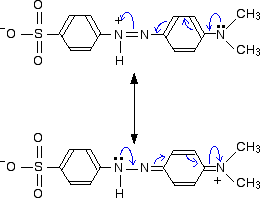
In reality, the electrons haven't shifted fully either one way or the other. Just as in the benzene case, the actual structure lies somewhere in between these.
You must also realize that drawing canonical forms has no effect on the underlying geometry of the structure. Bond types or lengths or angles don't change in the real structure.
For example, the lone pairs on the nitrogen atoms shown in the last diagram are both involved with the delocalisation. For this to happen all the bonds around these nitrogens must be in the same plane, with the lone pair sticking up so that it can overlap sideways with orbitals on the next-door atoms. The fact that in each of the two canonical forms one of these nitrogens is shown as if it had an ammonia-like arrangement of the bonds is potentially misleading - and makes it look as if the delocalization is broken.
The problem is that there is no easy way of representing a complex delocalized structure in simple structural diagrams. It is bad enough with benzene - with something as complicated as methyl orange any method just leads to possible confusion if you aren't used to working with canonical forms.
It gets even more complicated! If you were doing this properly there would be a host of other canonical forms with different arrangements of double and single bonds and with the positive charge located at various places around the rings and on the other nitrogen atom.
The real structure can't be represented properly by any one of this multitude of canonical forms, but each gives a hint of how the delocalization works.
If we take the two forms we have written as perhaps the two most important ones, it suggests that there is delocalization of the electrons over the whole structure, but that electron density is a bit low around the two nitrogens carrying the positive charge on one canonical form or the other.
Why is the red form more delocalized
Finally, we get around to an attempt at an explanation as to why the delocalization is greater in the red form of methyl orange in acid solution than in the yellow one in alkaline solution. The answer may lie in the fact that the lone pair on the nitrogen at the right-hand end of the structure as we've drawn it is more fully involved in the delocalization in the red form. The canonical form with the positive charge on that nitrogen suggests a significant movement of that lone pair towards the rest of the molecule.
Doesn't the same thing happen to the lone pair on the same nitrogen in the yellow form of methyl orange? Not to the same extent.
Any canonical form that you draw in which that happens produces another negatively charged atom somewhere in the rest of the structure. Separating negative and positive charges like this is energetically unfavourable. In the red form, we aren't producing a new separation of charge - just shifting a positive charge around the structure.

