5.10: Enantiomeric Excess
- Page ID
- 18056
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What do you notice about these three pictures? Count the number of left gloves and right gloves.

6 left and 6 right gloves, correct?
What about this one:
I count 8 right gloves, 4 left gloves. So there’s a slight excess of right gloves here.
Finally, this figure:
ONLY right hand gloves here. 12 right gloves, zero left gloves.
Application to organic chemistry?
Gloves are chiral objects. That is, they lack an internal plane of symmetry. Left gloves and right gloves are mirror images of each other, but they can’t be superimposed. In chemistry, there’s a word we have to describe a pair of non-superimposable mirror images – they’re called enantiomers.
Tying it back to the drawings, we can have three types of situations.
- Racemic Mixture: In the first drawing, we have an equal number of left and right gloves (i.e. enantiomers). This is called a racemic mixture of enantiomers.
- Enantiomeric excess: In the second drawing, we have an excess of right gloves compared to left gloves. In a situtation like this we can say we have an “enantiomeric excess” of gloves, or alternatively, the mixture is “enantioenriched” in the right-hand glove. [We can also calculate the "excess" here: the mixture is 66% right and 33% left - so we have a 33% "excess" of the right-hand enantiomer].
- Enantiomeric pure: In the third drawing, we have only right-hand gloves. This is said to be an “enantiomerically pure” mixture of gloves, since we have only one enantiomer present.

- A solution containing equal amounts of (R)-2-butanol and (S)-2-butanol is a racemic mixture.
- A solution containing an excess of either the (R)-enantiomer or the (S)-enantiomer would be enantioenriched.
- A solution containing only the (R)-enantiomer or the (S)-enantiomer will be enantiomerically pure.
Contributors
James Ashenhurst (MasterOrganicChemistry.com)
- A big thanks to Agnieszka at IlluScientia for the glove drawings.
4.5.1 Enantiomeric Excess and Optical Purity
Enantiomeric Excess
For non-racemic mixtures of enantiomers, one enantiomer is more abundant than the other. The composition of these mixtures is described by the enantiomeric excess, which is the difference between the relative abundance of the two enantiomers. Therefore, if a mixture contains 75% of the R enantiomer and 25% S, the enantiomeric excess if 50%. Similarly, a mixture that is 95% of one enantiomer, the enantiomeric excess is 90%, etc.
Enantiomeric excess is useful because it reflects the optical activity of the mixture. The standard optical rotation by the mixture (\([\alpha]_{mix}\)) is equal to the product of the standard optical rotation of the major isomer (\([\alpha]_{major}\)) and the enantiomeric excess (\(EE\)):
\[[\alpha]_{mix} = EE \times [\alpha]_{major}\]
In the same way, the enantiomeric excess in a mixture can be measured if the optical rotation of the pure enantiomer is known.
Diastereomeric Excess
A similar approach can be used to describe mixtures of diastereomers, resulting in the diastereomeric excess.
4.5.2 Resolution of Enantiomers
As noted earlier, chiral compounds synthesized from achiral starting materials and reagents are generally racemic (i.e. a 50:50 mixture of enantiomers). Separation of racemates into their component enantiomers is a process called resolution. Since enantiomers have identical physical properties, such as solubility and melting point, resolution is extremely difficult. Diastereomers, on the other hand, have different physical properties, and this fact is used to achieve resolution of racemates. Reaction of a racemate with an enantiomerically pure chiral reagent gives a mixture of diastereomers, which can be separated. Reversing the first reaction then leads to the separated enantiomers plus the recovered reagent.
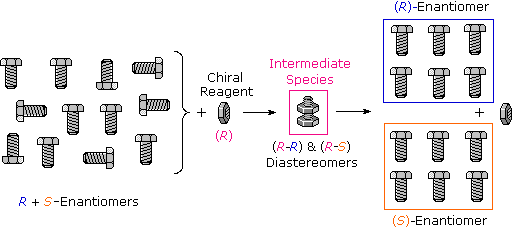
Many kinds of chemical and physical reactions, including salt formation, may be used to achieve the diastereomeric intermediates needed for separation. The following diagram illustrates this general principle by showing how a nut having a right-handed thread (R) could serve as a "reagent" to discriminate and separate a mixture of right- and left-handed bolts of identical size and weight. Only the two right-handed partners can interact to give a fully-threaded intermediate, so separation is fairly simple. The resolving moiety, i.e. the nut, is then removed, leaving the bolts separated into their right and left-handed forms. Chemical reactions of enantiomers are normally not so dramatically different, but a practical distinction is nevertheless possible.
To learn more about chemical procedures for achieving resolution Click Here.
Contributors
- William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
Further Reading on Enantiomeric Excess and Optical Purity
Carey 4th Edition On-Line Activity

