4.7: Stress-Strain Relationships
- Page ID
- 191182
If you think about materials made from polymers, a couple of things might readily come to mind. You might think about the ubiquitous use of plastics in structures around us, such as automobile bumpers. You might think about a rubber band that you use to fasten something more firmly, either at home or in the lab. In either case, the function of the material relies on its response to stimuli. Do we want it to be flexible, to change shape, but then snap back to where it came from? Exactly how much flexibility do we need? Where is the trade-off between flexibility and strength?
These questions are important in polymer chemistry. Consequently, we often need to probe how materials behave under different conditions so that we know how they can be employed most effectively.
Tensile testing is one of the simplest ways to probe how a material responds to stress. Remember, the stress in this context means the force exerted on the material per unit of cross-sectional area. As such, it has units of pressure, such as Pascals (Pa). To do the experiment, the two ends of a sample are attached to two clamps, one of which is movable. The movable clamp is then pulled so that the sample becomes stretched. The force required to pull the sample is recorded and, given the cross-sectional area of the sample perpendicular to the force, the force is converted into units of strain.

The experiment also measures the distance that the sample is stretched (the strain). That distance is usually expressed as a ratio, comparing the change in length to the original length of the sample. It can be written either as a fraction or as a percent.

In the rough sketch below, we can see what typically happens in such an experiment. The sample stretches (the strain increases), and it gets harder to stretch as seen by the increasing force (and therefore increasing stress) that is needed to keep stretching it. Eventually, the stress plummets, because of the sample breaks.
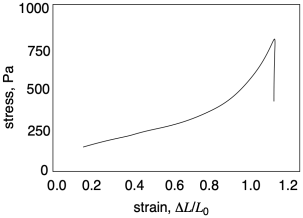
Already in this graph, we can see a couple of important pieces of information we can learn from tensile testing. Number one, how far can we stretch this material before it breaks? That quantity is called "strain at break". In this sample the strain at break looks like about 1.1 or 110%; that means the sample was stretched to twice its original length, and then some. Number two, how much stress can the sample support without breaking? That quantity is called "ultimate tensile strength". In this sample, the ultimate tensile strength is just over 750 Pa.
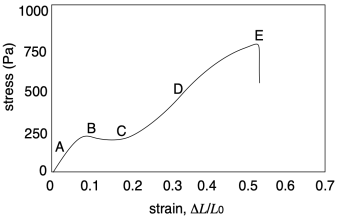
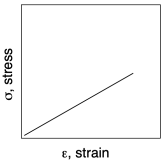
If we look more closely at the graph from another sample, we will get a third important quantity, and see some additional features. The important quantity can be derived from the first part of the curve (A), in which stress increases linearly with strain. In this linear region, the material is behaving as a "Hookean solid", meaning it obeys Hooke's Law. Hooke's Law says that stress and strain should be directly proportional. In his original words, the extension is proportional to the force:
F = kx
in which F is the force, x is the extension of the solid, and k is the proportionality constant.
Hooke's Law is commonly applied to the behavior of mechanical springs, but it also holds for other solid materials. The slope in the linear region of the graph (A) would equal that proportionality constant, k, because the graph shows the ratio of F/x. In materials science, this slope is more commonly called "Young's modulus". It is a measure of the inherent stiffness of the material.
Young's modulus: E = σ/ε
in which σ = stress and ε = extensional strain.
The extensional strain is just the strain observed by stretching the material. In the graph shown above, Young's modulus is around:
250 Pa / 0.1 = 2,500 Pa.
This initial region of the curve, in which Hooke's Law is obeyed, is sometimes called the "linear elastic region". The word "elastic" does have an immediate connotation in everyday English, bringing to mind a rubber band that can be stretched, so we think of the stretching part when we hear the word "elastic". However, the returning motion is an essential feature of elastic behavior. The rubber band always comes back to its original shape. Likewise, within the linear elastic region, any solid material returns to its original shape after it is deformed under stress.
With most solids, such as aluminum or concrete, the linear elastic region spans a very narrow range of strains. Just by looking, we wouldn't notice these materials being deformed. However, this linear stress-strain relationship is typical of solids. In rheology, that behavior is described as elastic. Of course, with many polymers, a sample can be stretched so far that you can see the change with the naked eye, and it still returns to that original shape.
What makes polymers different? The long-chain structure of polymers does make them behave differently from other materials. These chains can undergo conformational change: each bond along the chain can rotate, converting the polymer chain into a slightly different shape. That ability gives a "soft material" a great deal of flexibility. The conformations of chains can adapt to accommodate stress, moving the chains into new shapes that offer lower-energy packing between each other. When the stress is removed, the chains eventually slide back into their original conformations. They return to their equilibrium shapes.
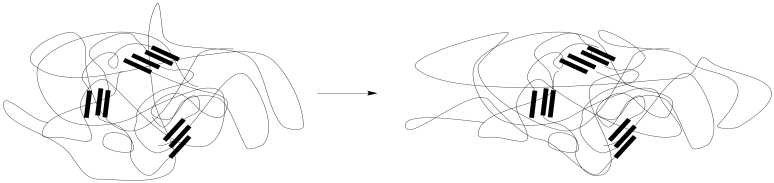
The presence of physical or chemical crosslinks help the material return to its original shape, functioning as anchor points so that the chains don't stray too far. Those interactions might be found in hard-phase interactions in a microphase separated material, as illustrated here, although they could also be found in a homogeneous material.
The linear elastic region isn't all we see in the stress-strain curve above. At point (B), the linear relationship is suddenly lost. The stress might even drop, as seen in this particular case. This feature on the graph is called the "yield point". The stress being experienced by the material, and the resulting strain, has become sufficient to overcome the natural elastic behavior of the solid. As noted previously, physical crosslinks such as hydrogen bonds help to reinforce the elastic behavior of a polymer sample. If, at some point, those interactions are overcome, the chains will start to slide more readily past each other.
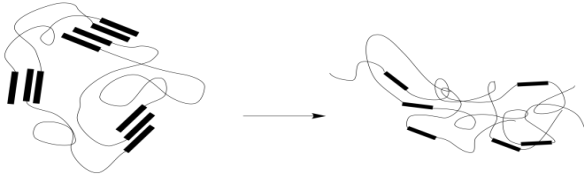
As a result, the material loses its elasticity. When the stress is released, the material will still spring back as the chains settle into a new conformational equilibrium. However, that equilibrium will not be the same as the one before. New physical crosslinks will form as groups form intermolecular interactions with the nearest neighbors they encounter. It isn't likely that these will always be the same groups that they were interacting with before. As a result, the material will settle into a slightly different shape. You have probably seen this happen before when a rubber band has been stretched too far, too often, or for too long. Chains have dropped their old interactions and picked up new ones that formed more easily in the extended shape.
At point (C) of the example graph, the slope of the curve starts to increase. The same change in stress results in smaller and smaller changes in strain; the material is getting stiffer. This phenomenon is called "strain hardening". This feature would not always be observed, but if it did happen, what would explain it? In polymers, one explanation may lay in the fact that the volume of the material should remain constant as it is stretched. If the sample is getting longer, that means it is also getting narrower.

As a consequence of that narrowing cross-section, chains become compressed together. At some point, physical crosslinks begin occurring between neighboring chains. These crosslinks don't occur in equilibrium positions, with polymer chains coiled around each other like they were in the original sample. These crosslinks occur when chains are extended, lying parallel to each other, at closer contact distances than normal.

We can see the opposite sort of thing happening at (D), when the slope of the curve is decreasing instead of increasing. This phenomenon is called "strain-softening". Again, it might not be observed in all samples. When it does happen, what causes it? In this case, the answer is simpler. Having overcome the interactions that held the chains together, there is nothing left to resist further deformation. As the chains begin to disentangle from each other, it becomes even easier to pull them apart, facilitating the extension or stretching of the sample.

Eventually, at the breaking point (E), the chains start to lose contact with each other at some location in the sample, resulting in a catastrophic rupture of the sample.
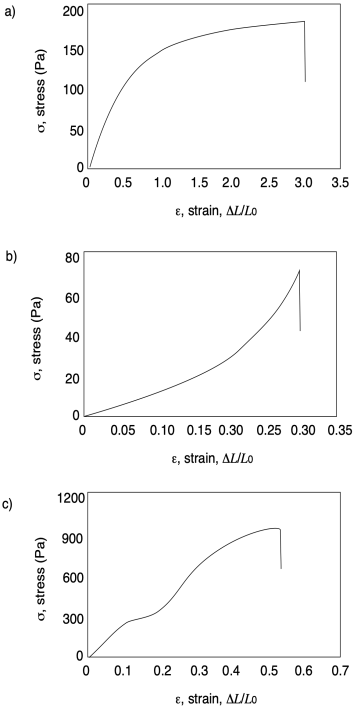
Problem PP7.1.
In each of the following curves, estimate ultimate tensile strength and strain at break.
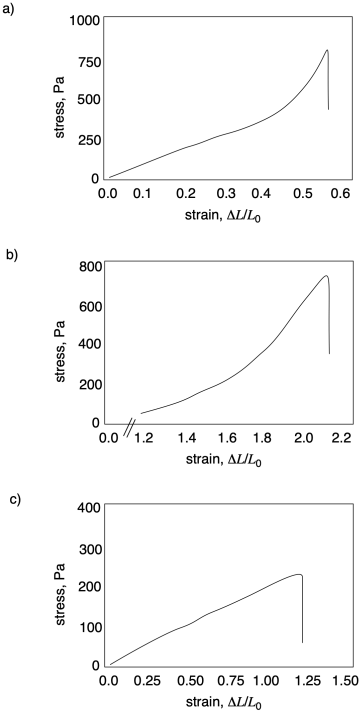
Problem PP7.2.
In each of the following curves, calculate Young's modulus.

Problem PP7.3.
In each of the following curves, identify any diagnostic features.