29.2: A Simple Addition Polymerization. The Parts of a Polymer
- Page ID
- 22393
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
The thermal polymerization of 1,3-cyclopentadiene by way of the Diels-Alder addition is not an important polymerization, but it does provide a simple concrete example of how a monomer and a polymer are related:
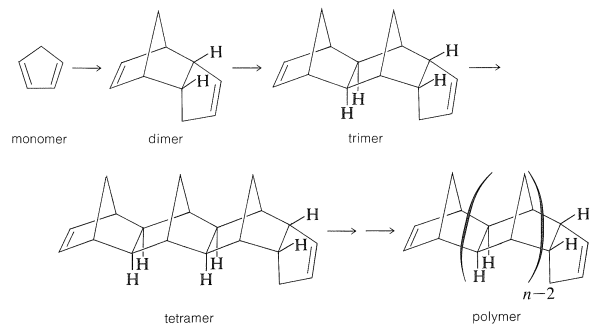
The first step in this polymerization is formation of the dimer, which involves 1,3-cyclopentadiene acting as both diene and dienophile. This step occurs readily on heating, but slowly at room temperature. In subsequent steps, 1,3-cyclopentadiene adds to the relatively strained double bonds of the bicyclo[2.2.1]heptene part of the polymer. These additions to the growing chain require higher temperatures (\(180\)-\(200^\text{o}\)). If cyclopentadiene is heated to \(200^\text{o}\) until substantially no further reaction occurs, the product is a waxy solid having a degree of polymerization \(n\) ranging from two to greater than six.
Polycyclopentadiene molecules have two different kinds of double bonds for end groups and a complicated backbone of saturated fused rings. The polymerization is reversible and, on strong heating, the polymer reverts to cyclopentadiene.
There are two commonly used and numerically different ways of expressing the average molecular weight of a polymer such as polycyclopentadiene. One is the number-average molecular weight, \(\overline{M_n}\), which is the total weight of a polymer sample, \(m\), divided by the total number of moles of molecules it contains, \(\Sigma N_i\). Thus
\[\overline{M_n} = \frac{m}{\Sigma N_i} = \frac{\Sigma \left( N_i M_i \right)}{\Sigma N_i}\]
in which \(N_i\) is the number of moles of a single kind of molecular species, \(i\), and \(M_i\) is the molecular weight of that species.
An alternative way of expressing the molecular weight is by the weight average, \(\overline{M_w}\), which can be computed by summing up the contribution (as measured by the weight fraction \(w_i\)) of each molecular species \(i\) and its molecular weight \(M_i\):
\[\overline{M_w} = \Sigma \left( w_i M_i \right)\]
The reason for using two different molecular weights is that some properties, such as freezing points, vapor pressure, and osmotic pressure of dilute solutions, are related directly to \(\overline{M_w}\), whereas other properties, such as light-scattering, sedimentation, and diffusion constants, are related directly to \(\overline{M_n}\).
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


