1.2: A Bit of History
- Page ID
- 22163
You may not be much interested in the way that organic chemistry developed, but if you skip to the next section without reading further, you will miss some of the flavor of a truly great achievement - of how a few highly creative chemists were able, with the aid of a few simple tools, to determine the structures of molecules, far too small and too elusive to be seen individually with the finest optical microscope, manifesting themselves only by the collective behavior of at least millions of millions at once.
Try to visualize the problems confronting the organic chemist of 100 years ago. You will have no more than reasonably pure samples of organic compounds, the common laboratory chemicals of today, glassware, balances, thermometers, means of measuring densities, and a few optical instruments. You also will have a relatively embryonic theory that there are molecules in those bottles and that one compound differs from another because its molecules have different members or kinds of atoms and different arrangements of bonds. Your task will be to determine what kinds and what numbers of atoms they contain, that is, to determine their molecular formulas. Obviously, a compound with formula \(C_2H_6O\) and one with \(C_2H_6O_2\) are not the same compound. But suppose two compounds from different sources both are \(C_2H_6O\). To decide whether these are the same or different you could smell them (far better to sniff than to inhale), taste them (emphatically not recommended), see if they have the same appearance and viscosity (if liquids), or use more sophisticated criteria: boiling point, melting point, density, or refractive index. Other possibilities would be to see if they both have the same solubility in water or other solvents and whether they give the same reaction products with various reagents. Of course, all this gets a bit tough when the compounds are not pure and no good ways are available to purify them, but that is part of the job. Think about how you might proceed.
In retrospect it is surprising that in less than fifty years an enormous, even if incomplete, edifice of structural organic chemistry was constructed on the basis of the results of chemical reactions without determination of a single bond distance, and with no electronic theory as a guide. Interestingly, all of the subsequent developments of the quantum mechanical theory of chemical bonds has not altered this edifice in significant ways. Indeed, for a long time, a goal of molecular quantum mechanics was simply to be able to corroborate that when an organic chemist draws a single line between two carbon atoms to show that they are bonded, he in fact knows what he is doing. And that when he draws two (or three) bonds between the carbons to indicate a double (or triple) bond, quantum mechanics supports this also as a valid idea.
Furthermore, when modern tools for determining organic structures that involve actually measuring the distances between the atoms became available, these provided great convenience, but no great surprises. To be sure, a few structures turned out to be incorrect because they were based on faulty or inadequate experimental evidence. But, on the whole, the modern three-dimensional representations of molecules that accord with actual measurements of bond distances and angles are in no important respect different from the widely used three-dimensional ball-and-stick models of organic molecules, and these, in essentially their present form, date from at least as far back as E. Paterno, in 1869.
How was all of this achieved? Not by any very simple process. The essence of some of the important ideas follow, but it should be clear that what actually took place was far from straightforward. A diverse group of people was involved; many firmly committed to, if not having a vested interest in, earlier working hypotheses or paradigms that had served as useful bases for earlier experimentation, but were coming apart at the seams because they could not accommodate the new facts that kept emerging. As is usual in human endeavors, espousal of new and better ideas did not come equally quickly to all those used to thinking in particular ways. To illustrate, at least one famous chemist, Berthelot, still used \(HO\) as the formula for water twenty-five years after it seemed clear that \(H_2O\) was a better choice.
Determination of Molecular Formulas
Before structures of molecules could be established, there had to be a means of establishing molecular formulas and for this purpose the key concept was Avogadro's hypothesis, which can be stated in the form "equal volumes of gases at the same temperature and pressure contain the same number of molecules." Avogadro's hypothesis allowed assignment of relative molecular weights from measurements of gas densities. Then, with analytical techniques that permit determination of the weight percentages of the various elements in a compound, it became possible to set up a self-consistent set of relative atomic weights.\(^1\) From these and the relative molecular weights, one can assign molecular formulas. For example, if one finds that a compound contains \(22.0 \%\) carbon (atomic weight \(= 12.00\)), \(4.6 \%\) hydrogen (atomic weight \(= 1.008\)), and \(73.4 \%\) bromine (atomic weight \(= 79.90\)), then the ratios of the numbers of atoms are \(\left( 22.0/12.00 \right) : \left( 4.6/1.008 \right) : \left( 73.4/79.90 \right) = 1.83:4.56:0.92\). Dividing each of the last set of numbers by the smallest (\(0.92\)) gives \(1.99:4.96:1 \cong 2:5:1\), which suggests a molecular formula of \(C_2H_5Br\) or a multiple thereof. If we know that hydrogen gas is \(H_2\) and has a molecular weight of \(2 \times 1.008 = 2.016\), we can compare the weight of a given volume of hydrogen with the weight of the same volume of our unknown in the gas phase at the same temperature and pressure. If the experimental ratio of these weights turns out to be \(54\), then the molecular weight of the unknown would be \(2.016 \times 54 = 109\) and the formula \(C_2H_5Br\) would be correct.
Valence
If we assume that the molecule is held together by chemical bonds, without knowing more, we could write numerous structures such as \(H-H-H-H-H-C-C-Br, H-C-Br-H-H-C-H-H\), and so on. However, if we also know of the existence of stable \(H_2\), but not \(H_3\); of stable \(Br_2\), but not of \(Br_3\); and of stable \(CH_3Br\), \(CH_2Br_2\), \(CHBr_3\), and \(CBr_4\), but not of \(CH_4Br\), \(CHBr\), \(CBr\), and so on, a pattern of what is called valence emerges. It will be seen that the above formulas all are consistent if hydrogen atoms and bromine atoms form just one bond (are univalent) while carbon atoms form four bonds (are tetravalent). This may seem almost naively simple today, but a considerable period of doubt and uncertainty preceded the acceptance of the idea of definite valences for the elements that emerged about 1852.
Structural Formulas
If we accept hydrogen and bromine as being univalent and carbon as tetravalent, we can write
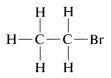
as a structural formula for \(C_2H_5Br\).\(^2\) However, we also might have written
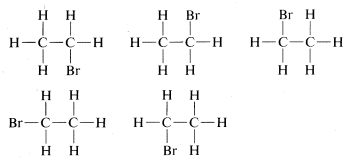
There is a serious problem as to whether these formulas represent the same or different compounds. All that was known in the early days was that every purified sample of \(C_2H_5Br\), no matter how prepared, had a boiling point of \(38^\text{o}C\) and density of \(1.460 \: \text{g} \: \text{ml}^{-1}\). Furthermore, all looked the same, all smelled the same, and all underwent the same chemical reactions. There was no evidence that \(C_2H_5Br\) was a mixture or that more than one compound of this formula could be prepared. One might conclude, therefore, that all of the structural formulas above represent a single substance even though they superficially, at least, look different. Indeed, because \(H-Br\) and \(Br-H\) are two different ways of writing a formula for the same substance, we suspect that the same is true for
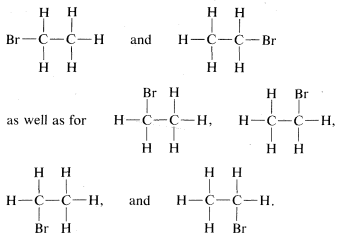
There are, though, two of these structures that could be different from one another, namely
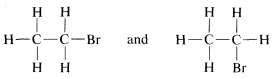
In the first of these, \(CH_3-\) is located opposite the \(Br-\) and the \(H-\)'s on the carbon with the \(Br\) also are opposite one another. In the second formula, \(CH_3-\) and \(Br-\) are located next to each other as are the \(H-\)'s on the same carbon. We therefore have a problem as to whether these two different formulas also represent different compounds.
Tetrahedral Carbon
A brilliant solution to the problem posed in the preceding section came in 1874 when J. H. van't Hoff proposed that all four valences of carbon are equivalent and directed to the corners of a regular tetrahedron.\(^3\) If we redraw the structures for \(C_2H_5Br\) as \(1\), we see that there is only one possible arrangement and, contrary to the impression we got from our earlier structural formulas, the bromine is equivalently located with respect to each of the hydrogens on the same carbon.
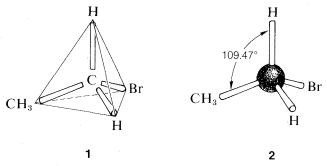
A convenient way of representing organic molecules in three dimensions, which shows the tetrahedral relationships of the atoms very clearly, uses the so-called ball-and-stick models. The sticks that represent the bonds or valences form the tetrahedral angles of \(109.47^\text{o}\).
The Question of Rotational Isomers
The tetrahedral carbon does not solve all problems without additional postulates. For example, there are two different compounds known with the same formula \(C_2H_4Br_2\). These substances, which we call isomers, can be reasonably written as
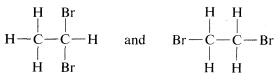
However, ball-and-stick models suggest further possibilities for the second structure, for example \(3\), \(4\), and \(5\):
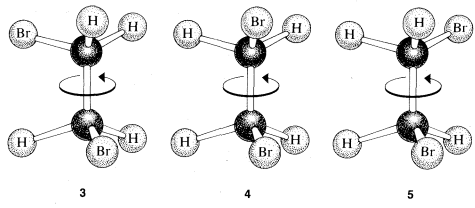
This is a problem apparently first clearly recognized by Paterno, in 1869. We call these rotational (or conformational) isomers, because one is converted to another by rotation of the halves of the molecule with respect to one another, with the \(C-C\) bond acting as an axle. If this is not clear, you should make a ball-and-stick model and see what rotation around the \(C-C\) bond does to the relationships between the atoms on the carbons.
The difficulty presented by these possibilities finally was circumvented by a brilliant suggestion by van't Hoff of "free rotation," which holds that isomers corresponding to different rotational angles, such as \(3\), \(4\), and \(5\), do not have separate stable existence, but are interconverted by rotation around the \(C-C\) bond so rapidly that they are indistinguishable from one another. Thus there is only one isomer corresponding to the different possible rotational angles and a total of only two isomers of formula \(C_2H_4Br_2\). As we shall see, the idea of free rotation required extensive modification some 50 years after it was first proposed, but it was an extremely important paradigm, which, as often happens, became so deeply rooted as to become essentially an article of faith for later organic chemists. Free rotation will be discussed in more detail in Chapters 5 and 27.
The Substitution Method for Proof of Structure
The problem of determining whether a particular isomer of \(C_2H_4Br_2\) is

could be solved today in a few minutes by spectroscopic means, as will be explained in Chapter 9. However, at the time structure theory was being developed, the structure had to be deduced on the basis of chemical reactions, which could include either how the compound was formed or what it could be converted to. A virtually unassailable proof of structure, where it is applicable, is to determine how many different substitution products each of a given group of isomers can give. For the \(C_2H_4Br_2\) pair of isomers, substitution of a bromine for a hydrogen will be seen to give only one possibility with one compound and two with the other:
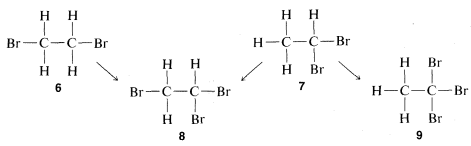
Therefore, if we have two bottles, one containing one \(C_2H_4Br_2\) isomer and one the other and run the substitution test, the compound that gives only one product is \(6\) and the one that gives a mixture of two products is \(7\). Further, it will be seen that the test, besides telling which isomer is \(6\) and which is \(7\), establishes the structures of the two possible \(C_2H_3Br_3\) isomers, \(8\) and \(9\). Thus only \(8\) can be formed from both of the different \(C_2H_4Br_2\) isomers whereas \(9\) is formed from only one of them.
The Benzene Problem
There were already many interconversion reactions of organic compounds known at the time that valence theory, structural formulas, and the concept of the tetrahedral carbon came into general use. As a result, it did not take long before much of organic chemistry could be fitted into a concordant whole. One difficult problem was posed by the structures of a group of substitution products of benzene, \(C_6H_6\), called "aromatic compounds," which for a long time defied explanation. Benzene itself had been prepared first by Michael Faraday, in 1825. An ingenious solution for the benzene structure was provided by A. Kekule, in 1866, wherein he suggested (apparently as the result of a hallucinatory perception) that the six carbons were connected in a hexagonal ring with alternating single and double carbon-to-carbon bonds, and with each carbon connected to a single hydrogen, \(10\):
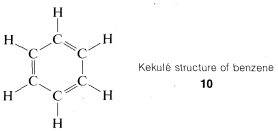
This concept was controversial, to say the least, mainly on two counts. Benzene did not behave as expected, as judged by the behavior of other compounds with carbon-to-carbon double bonds and also because there should be two different dibromo substitution products of benzene with the bromine on adjacent carbons (\(11\) and \(12\)) but only one such compound could be isolated.
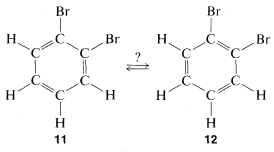
Kekule explained the second objection away by maintaining that \(11\) and \(12\) were in rapid equilibrium through concerted bond shifts, in something like the same manner as the free-rotation hypothesis mentioned previously:
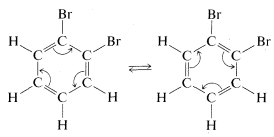
However, the first objection could not be dismissed so easily and quite a number of alternative structures were proposed over the ensuing years. The controversy was not really resolved until it was established that benzene is a regular planar hexagon, which means that all of its \(C-C\) bonds have the same length, in best accord with a structure written not with double, not with single, but with 1.5 bonds between the carbons, as in \(13\):
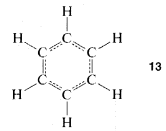
This. in turn, generated a massive further theoretical controversy over just how \(13\) should be interpreted, which, for a time, even became a part of "Cold-War" politics!\(^4\) We shall examine experimental and theoretical aspects of the benzene structure in some detail later. It is interesting that more than 100 years after Kekule's proposal the final story on the benzene structure is yet to be told.\(^5\)
Proof of Structure through Reactions
The combination of valence theory and the substitution method as described in Section 1-1F gives, for many compounds, quite unequivocal proofs of structure. Use of chemical transformations for proofs of structure depends on the applicability of a simple guiding principle, often called the "principle of least structural change." As we shall see later, many exceptions are known and care is required to keep from making serious errors. With this caution, let us see how the principle may be applied. The compound \(C_2H_5Br\) discussed in Section 1-1A reacts slowly with water to give a product of formula \(C_2H_6O\). The normal valence of oxygen is two, and we can write two, and only two, different structures, \(19\) and \(20\), for \(C_2H_6O\):
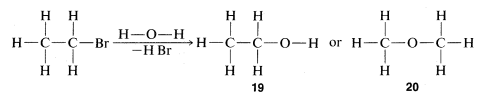
The principle of least structural change favors \(19\) as the product, because the reaction to form it is a simple replacement of bromine bonded to carbon by \(-OH\), whereas formation of \(20\) would entail a much more drastic rearrangement of bonds. The argument is really a subtle one, involving an assessment of the reasonableness of various possible reactions. On the whole, however, it works rather well and, in the specific case of the \(C_2H_6O\) isomers, is strongly supported by the fact that treatment of \(19\) with strong hydrobromic acid (\(HBr\)) converts it back to \(C_2H_5Br\). In contrast, the isomer of structure \(20\) reacts with \(HBr\) to form two molecules of \(CH_3Br\):

In each case, \(C-O\) bonds are broken and \(C-Br\) bonds are formed.
We could conceive of many other possible reactions of \(C_2H_6O\) with \(HBr\), for example
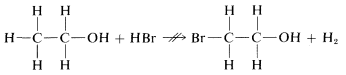
which, as indicated by \(\nrightarrow\), does not occur, but hardly can be ruled out by the principle of least structural change itself. Showing how the probability of such alternative reactions can be evaluated will be a very large part of our later discussions.
Reactivity, Saturation, Unsaturation, and Reaction Mechanisms
The substitution method and the interconversion reactions discussed for proof of structure possibly may give you erroneous ideas about the reactions and reactivity of organic compounds. We certainly do not wish to imply that it is a simple, straightforward process to make all of the possible substitution products of a compound such as
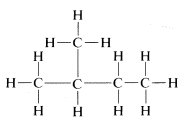
In fact, as will be shown later, direct substitution of bromine for hydrogen with compounds such as this does not occur readily, and when it does occur, the four possible substitution products indeed are formed, but in far from equal amounts because there are differences in reactivity for substitution at the different positions. Actually, some of the substitution products are formed only in very small quantities. Fortunately, this does not destroy the validity of the substitution method but does make it more difficult to apply. If direct substitution fails, some (or all) of the possible substitution products may have to be produced by indirect means. Nonetheless, you must understand that the success of the substitution method depends on determination of the total number of possible isomers - it does not depend on how the isomers are prepared.
Later, you will hear a lot about compounds or reagents being "reactive" and "unreactive." You may be exasperated by the loose way that these terms are used by organic chemists to characterize how fast various chemical changes occur. Many familiar inorganic reactions, such as the neutralization of hydrochloric acid with sodium hydroxide solution, are extremely fast at ordinary temperatures. But the same is not often true of reactions of organic compounds. For example, \(C_2H_5Br\) treated in two different ways is converted to gaseous compounds, one having the formula \(C_2H_6\) and the other \(C_2H_4\). The \(C_2H_4\) compound, ethene, reacts very quickly with bromine to give \(C_2H_4Br_2\), but the \(C_2H_6\) compound, ethane, does not react with bromine except at high temperatures or when exposed to sunlight (or similar intense light). The reaction products then are \(HBr\) and \(C_2H_5Br\), and later, \(HBr\) and \(C_2H_4Br_2\), \(C_2H_3Br_3\), and so on.
We clearly can characterize \(C_2H_4\) as "reactive" and \(C_2H_6\) as "unreactive" toward bromine. The early organic chemists also used the terms "unsaturated" and "saturated" for this behavior, and these terms are still in wide use today. But we need to distinguish between "unsaturated" and "reactive," and between "saturated" and "unreactive," because these pairs of terms are not synonymous. The equations for the reactions of ethene and ethane with bromine are different in that ethene adds bromine, \(C_2H_4 + Br_2 \rightarrow C_2H_4Br_2\), whereas ethane substitutes bromine, \(C_2H_6 + Br_2 \rightarrow C_2H_5Br + HBr\).
You should reserve the term "unsaturated" for compounds that can, at least potentially, react by addition, and "saturated' for compounds that can only be expected to react by substitution. The difference between addition and substitution became much clearer with the development of the structure theory that called for carbon to be tetravalent and hydrogen univalent. Ethene then was assigned a structure with a carbon-to-carbon double bond, and ethane a structure with a carbon-to-carbon single bond:
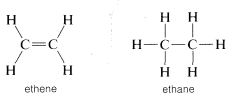
Addition of bromine to ethene subsequently was formulated as breaking one of the carbon-carbon bonds of the double bond and attaching bromine to these valences. Substitution was written similarly but here bromine and a \(C-H\) bond are involved:
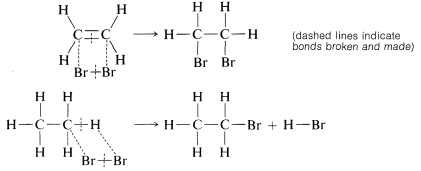
We will see later that the way in which these reactions actually occur is much more complicated than these simple equations indicate. In fact, such equations are regarded best as chemical accounting operations. The number of bonds is shown correctly for both the reactants and the products, and there is an indication of which bonds break and which bonds are formed in the overall process. However, do not make the mistake of assuming that no other bonds are broken or made in intermediate stages of the reaction.
Much of what comes later in this book will be concerned with what we know, or can find out, about the mechanisms of such reactions - a reaction mechanism being the actual sequence of events by which the reactants become converted to the products. Such information is of extraordinary value in defining and understanding the range of applicability of given reactions for practical preparations of desired compounds.
The distinction we have made between "unsaturated" and "reactive" is best illustrated by a definite example. Ethene is "unsaturated" (and "reactive") toward bromine, but tetrachloroethene, \(C_2Cl_4\), will not add bromine at all under the same conditions and is clearly "unreactive." But is it also "saturated"?
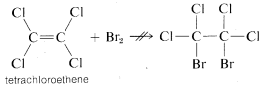
The answer is definitely no, because if we add a small amount of aluminum bromide, \(AlBr_3\), to a mixture of tetrachloroethene and bromine, addition does occur, although sluggishly:
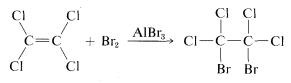
Obviously, tetrachloroethene is "unsaturated" in the sense it can undergo addition, even if it is unreactive to bromine in the absence of aluminum bromide.
The aluminum bromide functions in the addition of bromine to tetrachloroethene as a catalyst, which is something that facilitates the conversion of reactants to products. The study of the nature and uses of catalysts will concern us throughout this book. Catalysis is our principal means of controlling organic reactions to help form the product we want in the shortest possible time.
\(^1\)We will finesse here the long and important struggle of getting a truly self-consistent table of atomic weights. If you are interested in the complex history of this problem and the clear solution to it proposed by S. Cannizzaro in 1860, there are many accounts available in books on the history of chemistry. One example is J. R. Partington, A History of Chemistry, Vol. IV, Macmillan, London, 1964. Relative atomic weights now are based on \(^{12}C = 12\) (exactly).
\(^2\)Formulas such as this appear to have been used first by Crum Brown, in 1864, after the originators of structural formulas, A. Kekule and A. Couper (1858), came up with rather awkward, impractical representations. It seems incredible today that even the drawing of these formulas was severely criticized for many years. The pot was kept boiling mainly by H. Kolbe, a productive German chemist with a gift for colorful invective and the advantage of a podium provided by being editor of an influential chemical journal.
\(^3\)The name of J. A. Le Bel also is associated with this particular idea, but the record shows that Le Bel actually opposed the tetrahedral formulations, although, simultaneously with van't Hoff, he made a related very important contribution, as will be discussed in Chapter 5.
\(^4\)The "resonance theory," to be discussed in detail in Chapters 6 and 21, was characterized in 1949 as a physically and ideologically inadmissible theory formulated by "decadent bourgeois scientists." See L. R. Graham, Science and Philosophy in the Soviet Union, Vintage Books, New York, 1973, Chapter VIII, for an interesting account of this controversy.
\(^5\)Modern organic chemistry should not be regarded at all as a settled science, free of controversy. To be sure, personal attacks of the kind indulged in by Kolbe and others often are not published, but profound and indeed acrimonious differences of scientific interpretation exist and can persist for many years.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


