16.13: Freezing Point Depression
- Page ID
- 53861
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Colligative properties have practical applications, such as the salting of roads in cold-weather climates. By applying salt to an icy road, the melting point of the ice is decreased, and the ice will melt more quickly, making driving safer. Sodium chloride \(\left( \ce{NaCl} \right)\), and either calcium chloride \(\left( \ce{CaCl_2} \right)\) or magnesium chloride \(\left( \ce{MgCl_2} \right)\) are used most frequently, either alone or in a mixture. Sodium chloride is the least expensive option, but is less effective because it only dissociates into two ions, instead of three.
Freezing Point Depression
The figure below shows the phase diagram for a pure solvent and how it changes when a solute is added to it. The solute lowers the vapor pressure of the solvent, resulting in a lowering of the freezing point of the solution compared to the solvent. The freezing point depression is the difference in temperature between the freezing point of the pure solvent and that of the solution. On the graph, the freezing point depression is represented by \(\Delta T_f\).
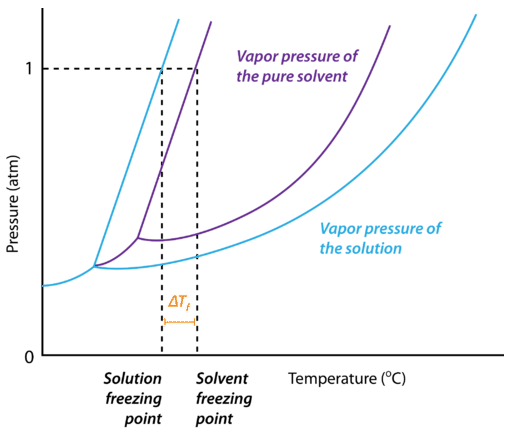
When a pure solvent freezes, its particles become more ordered as the intermolecular forces that operate between the molecules become permanent. In the case of water, the hydrogen bonds make the hexagonally-shaped network of molecules that characterizes the structure of ice. By dissolving a solute into the liquid solvent, this ordering process is disrupted. As a result, more energy must be removed from the solution in order to freeze it, and the freezing point of the solution is lower than that of the pure solvent.
The magnitude of the freezing point depression is directly proportional to the molality of the solution. The equation is:
\[\Delta T_f = K_f \times \textit{m}\nonumber \]
The proportionality constant, \(K_f\), is called the molal freezing-point depression constant. It is a constant that is equal to the change in the freezing point for a 1-molal solution of a nonvolatile molecular solute. For water, the value of \(K_f\) is \(-1.86^\text{o} \text{C}/\textit{m}\). So, the freezing temperature of a 1-molal aqueous solution of any nonvolatile molecular solute is \(-1.86^\text{o} \text{C}\). Every solvent has a unique molal freezing-point depression constant. These are shown in the table below, along with a related value for the boiling point called \(K_b\).
| Table \(\PageIndex{1}\): Molal Freezing-Point and Boiling-Point Constants | ||||
|---|---|---|---|---|
| Solvent | Normal Freezing Point \(\left( ^\text{o} \text{C} \right)\) | Molal Freezing-Point Depression Constant, \(K_f\) \(\left( ^\text{o} \text{C}/\textit{m} \right)\) | Normal Boiling Point \(\left( ^\text{o} \text{C} \right)\) | Molal Boiling-Point Elevation Constant, \(K_b\) \(\left( ^\text{o} \text{C}/\textit{m} \right)\) |
| Acetic acid | 16.6 | -3.90 | 117.9 | 3.07 |
| Camphor | 178.8 | -39.7 | 207.4 | 5.61 |
| Naphthalene | 80.2 | -6.94 | 217.7 | 5.80 |
| Phenol | 40.9 | -7.40 | 181.8 | 3.60 |
| Water | 0.00 | -1.86 | 100.00 | 0.512 |
Example \(\PageIndex{1}\)
Ethylene glycol \(\left( \ce{C_2H_6O_2} \right)\) is a molecular compound that is used in many commercial antifreezes. A water solution of ethylene glycol is used in vehicle radiators to lower its freezing point, and thus prevent the water in the radiator from freezing. Calculate the freezing point of a solution of \(400 \: \text{g}\) of ethylene glycol in \(500 \: \text{g}\) of water.
Solution
Step 1: List the known quantities and plan the problem.
Known
- Mass \(\ce{C_2H_6O_2} = 400 \: \text{g}\)
- Molar mass \(\ce{C_2H_6O_2} = 62.08 \: \text{g/mol}\)
- Mass \(\ce{H_2O} = 500 \: \text{g} = 0.500 \: \text{kg}\)
- \(K_f \left( \ce{H_2O} \right) = -1.86^\text{o} \text{C}/\textit{m}\)
Unknown
This is a three-step problem. First, calculate the moles of ethylene glycol. Then, calculate the molality of the solution. Finally, calculate the freezing point depression.
Step 2: Solve.
\[\begin{align*} 400. \: \text{g} \: \ce{C_2H_6O_2} \times \frac{1 \: \text{mol} \: \ce{C_2H_6O_2}}{62.08 \: \text{g} \: \ce{C_2H_6O_2}} &= 6.44 \: \text{mol} \: \ce{C_2H_6O_2} \\ \frac{6.44 \: \text{mol} \: \ce{C_2H_6O_2}}{0.500 \: \text{kg} \: \ce{H_2O}} &= 12.9 \: \textit{m} \: \ce{C_2H_6O_2} \\ \Delta T_f = K_f \times \textit{m} = -1.86^\text{o} \text{C}/\textit{m} &= -24.0^\text{o} \text{C} \\ T_f &= -24.0^\text{o} \text{C} \end{align*}\nonumber \]
The normal freezing point of water is \(0.0^\text{o} \text{C}\). Therefore, since the freezing point decreases by \(24.0^\text{o} \text{C}\), the freezing point of the solution is \(-24.0^\text{o} \text{C}\).
Step 3: Think about your result.
The freezing point of the water decreases by a large amount, protecting the radiator from damage due to the expansion of water when it freezes. There are three significant figures in the result.
Summary
- The freezing point depression is the difference in temperature between the freezing point of the pure solvent and that of the solution.
- The molal freezing-point depression constant is equal to the change in the freezing point for a 1-molal solution of a nonvolatile molecular solute.
- Calculations involving freezing point depression are described.

