Superconductivity refers to the flow of electrical current in a material with zero resistance. Such materials are very important for use in electromagnets, e.g., in magnetic resonance imaging (MRI) and nuclear magnetic resonance (NMR) machines, because once the current starts flowing in the coils of these magnets it doesn't stop. Magnetic levitation using superconductors - which, below a critical field strength, are perfect diamagnets that are not penetrated by magnetic flux lines - is also potentially relevant to future technologies such as magnetically levitated trains.
The phenomenon of superconductivity, first discovered in Hg metal in 1911 by Onnes, continues to be only partially understood. It is of great interest to physicists as a macroscopic quantum phenomenon, and to chemists and materials scientists who try to make better superconductors (especially those that superconduct at higher temperatures) and devices derived from them, such as superconducting quantum interference devices (SQUIDs), which are extremely sensitive magnetometers.
|

A magnet levitating above a high-temperature superconductor, cooled with liquid nitrogen. Persistent electric current flows on the surface of the superconductor, excluding the magnetic field of the magnet. This current effectively forms an electromagnet that repels the magnet.
|
Spin pairing and zero resistance
The transition from the metallic to the superconducting state is related to the quantum phenomena of Bose-Einstein condensation and superfluidity. Individual electrons have spin = 1/2, and as such are fermions (particles with half-integer spin). Because of the Pauli exclusion principle, no more than two fermions can occupy the same quantum state (such as an orbital in a molecule or a solid). The familiar consequence of this rule is the aufbau filling of orbitals with spin-paired electrons in each energy level. In contrast, particles with integer spins - which are called bosons - do not have this restriction, and any number of bosons can occupy the same quantized energy level.
Superconductivity occurs when electrons spin pair into so-called Cooper pairs, which can travel through the lattice together. The electrons in a Cooper pair, although spin-paired, have a long-distance relationship: the spatial extent of a Cooper pair is a few nanometers in cuprate superconductors, and up to one micron in low Tc superconductors such as aluminum. Because its overall spin angular momentum is zero, a Cooper pair is a boson. When the temperature is low enough, the Cooper pairs "condense" into the lowest energy level. The second lowest energy level - which is typically a few meV above the ground state - is not accessible to them as long as the energy gap is larger than the thermal energy, kT. The scattering of electrons by the lattice then becomes forbidden by energy conservation because scattering dissipates energy, and the Cooper pairs cannot change their energy state. Thus the resistance (which arises from scattering, as we learned in Ch. 6) drops abruptly to zero below Tc. However, the Cooper pairs can be broken apart when they move fast, and thus superconductors turn back into normal metals (even below Tc) above some critical current density jc. This phenomenon is also related to the critical magnetic field, Hc, that quenches superconductivity.
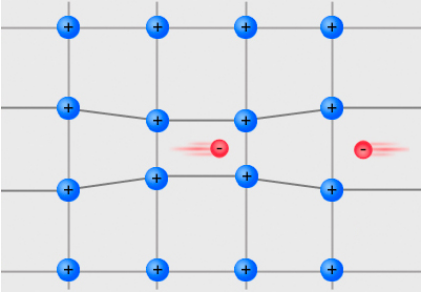
A trampoline for electrons
What causes electrons, which repel each other because of their negative charge, to pair up and travel together in superconductors? The mechanism - which must involve some kind of attractive interaction between electrons - is well understood for "conventional" superconductors which have relatively low transition temperatures, but is not yet known with certainty for high temperature oxide superconductors. In conventional, or BCS superconductors, the spin pairing is mediated by the lattice as shown in the figure at the left. A strong electron-lattice interaction causes a distortion in the lattice as an electron moves through. This elastic deformation is felt as an attractive force by a second electron moving in the opposite direction. This can be thought of as analogous to the interaction of two people jumping on a trampoline. The weight of the first person on the trampoline creates a "well" that attracts the second one, and they tend to move together (even if they don't like each other). Strange as this interaction seems, it is supported experimentally by isotope effects on Tc and by quantitative predictions of Tc values in conventional superconductors.
Bad metals make good superconductors. All superconductors are "normal" metals - with finite electrical resistance - above their critical transition temperature, Tc. If you ask where in the periodic table one might look for superconductors, the answer is surprising. The most conductive metals (Ag, Au, Cu, Cs, etc.) make the worst superconductors, i.e., they have the lowest superconducting transition temperatures, in many cases below 0.01 K. Conversely "bad" metals, such as niobium alloys, certain copper oxides, KxBa1-xBiO3, MgB2, FeSe, and alkali salts of C60n- anions, can have relatively high transition temperatures.
|
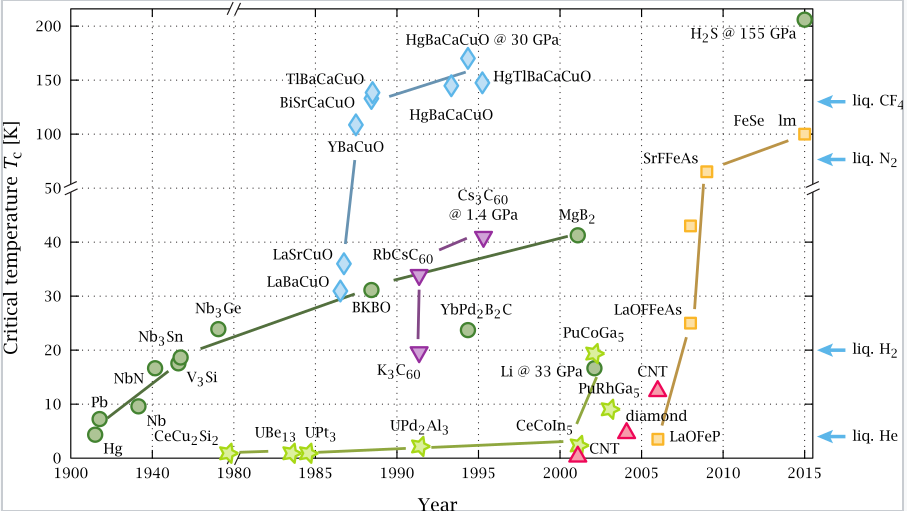
Timeline of superconducting materials, showing Tc vs. year of discovery.
|
We observe that most good superconductors appear in composition space very near a metal-insulator transition. In terms of our microscopic picture, orbital overlap in superconductors is poor, just barely enough to make them act as metals (Δ ≈ U) above Tc. In the normal state, superconductors with high Tc - which can be as high as 150 K - are typically "bad" metals. An important characteristic of such metals is that the mean free path of electrons (in the normal state, above Tc) is on the order of the lattice spacing, i.e., only a few Å. In contrast, we learned in Ch. 6 that good metals such as Au, Ag, and Cu have electron mean free paths that are two orders of magnitude longer (ca. 40 nm). In a bad metal, the electron "feels" the lattice rather strongly, whereas in a good metal, the electrons are insensitive to small changes in the distance between metals atoms.
What does the band picture look like for a bad metal? The key point is that because orbital overlap is poor, the metal has a high density of states at the Fermi level. This is a universal property of high temperature superconductors and provides a clue of where to look for new and improved superconducting materials. Recall that transition elements in the middle of the 3d series (Cr, Fe, Co, Ni) were magnetic because of poor orbital overlap and weak d-d bonding. The elements below these - especially Nb, Ta, and W - have just barely enough d-d orbital overlap to be on the metallic side of the metal-insulator transition and to be "bad" metals. Carbides and nitrides of these elements are typically superconducting, with the carbon and nitrogen atoms serving to adjust the valence electron density, as illustrated in the table below.
|
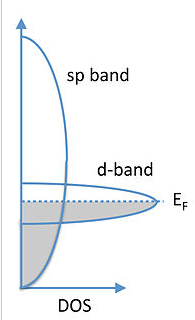
Generic E vs. DOS for a bad metal.
|
| Compound |
NbC |
Mo2N |
TaC |
VN |
NbN |
TaN |
Nb3Ge |
| Tc (K) |
11.1 |
5.0 |
9.7 |
7.5 |
15.2 |
17.8 |
22.3 |
High Tc superconductors
In addition to having weak orbital overlap in the metallic state - which results in a high DOS at EF - high temperature superconductors also typically contain elements in mixed oxidation states (for example, Cu2+/3+ or Bi3+/5+) that are close in energy to the O2-/O- couple in the lattice. At ambient pressure, cuprate superconductors have the highest known Tc values, ranging between about 35 and 150 K. The crystal structures of these materials are almost all variants of the perovskite lattice, as shown at the right for the 1-2-3 superconductor YBa2Cu3O7-δ. An ideal perovskite lattice would have formula ABO3 = A3B3O9. In YBa2Cu3O7-δ, Y and Ba occupy the A cation sites, Cu occupies the B sites, and two of the nine O atoms are missing.
The YBa2Cu3O7-δ lattice consists of mixed-valent copper(II/III) oxide sheets capped by oxygen atoms to form CuO5 square pyramids. These sheets encapsulate the Y3+ cations. Copper(II) oxide ribbons that share the apical oxygen atoms of the square pyramids run in one direction through the structure. In YBa2Cu3O7-δ and related materials, one component of the structure (here the Cu-O ribbons) acts as a charge reservoir to control the doping of the planar CuO2 sheets, which are the elements of the structure that carry the supercurrent. Cuprate superconductors with Bi, Tl, or Hg-containing charge reservoir layers and multiple, eclipsed CuO2 sheets in the unit cell tend to have the highest Tc values.
|
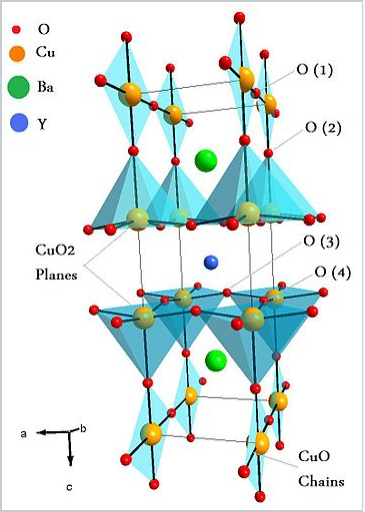
Crystal structure of YBa2Cu3O7-δ (YBCO), the first superconductor with Tc above the boiling point of liquid nitrogen.
|
The connection between the metal-insulator transtion and superconductivity is nicely illustrated in the phase diagram of La2-xSrxCuO4, the first cuprate superconductor, which was discovered in 1986 by Georg Bednorz and K. Alex Müller. This compound has a rather simple structure in which rocksalt La(Sr)O layers are intergrown with perovskite La(Sr)CuO3 layers. Undoped La2CuO4 contains only Cu2+ ions and is an antiferromagnetic insulator. As a small amount of Sr2+ is substituted for La3+, some of the Cu2+ is oxidized to Cu3+, and the lattice is doped with holes. As the doping level increases, the antiferromagnetic phase undergoes a first-order phase transition to a "bad" metal, and at slightly higher doping density the superconducting phase appears. The proximity of the superconducting phase to the metal-insulator transition is a hallmark of cuprate superconductors. A maximum Tc of 35K is observed at x = 0.15. Doping at higher levels moves the Fermi level beyond the point of highest DOS in the d-band of Cu and the superconducting phase then gradually disappears. It is interesting to compare this phase diagram with that of V2O3 (above), which also undergoes an antiferromagnetic insulator to "bad" metal transition as it is doped.
|

Crystal structure and phase diagram of the cuprate superconductor La2-xSrxCuO4. (LSCO)
|







