6.3.7: The Acidity of an Oxoacid is Determined by the Electronegativity and Oxidation State of the Oxoacid's Central Atom*
- Page ID
- 157377
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Oxyacids (also known as oxoacids) are compounds of the general formula \(\ce{H_{n}EO_{m}}\), where \(\ce{E}\) is a nonmetal or early transition metal and the acidic hydrogens are attached directly to oxygen (not \(\ce{E}\)). This class of compounds includes such well-know acids as nitric acid (\(\ce{HNO_2}\)) and phosphoric acid, (\(\ce{H_3PO_4}\)).

The acidity of oxyacids follows three trends:
Trend 1: In a homologous series the acidity increases with the electronegativity of the central atom
Elements in the same group frequently form oxyacids of the same general formula. For example, chlorine, bromine, and iodine all form oxyacids of formula \(\ce{HOE}\): hypochlorous, hypobromous and hypoiodous acids. In the case of these homologous oxyacids, the acidity is largely determined by the electronegativity of the central element. Central atoms that are better able to inductively pull electron density towards themselves make the oxygen-hydrogen bond that is to be ionized more polar and stabilize the conjugate base, \(OE^-\). Thus the acid strength in such homologous series increases with the electronegativity of the central atom. This may be seen from the data for the hypohalous acids in Table \(\PageIndex{1}\), in which the acid strength increases with the electronegativity of the halogen so that the order of acidity is:
\[\ce{HClO>HBrO>HIO} \nonumber \]
| HOX | Electronegativity of X | Ka |
|---|---|---|
| HOCl | 3.0 | 4.0 × 10−8 |
| HOBr | 2.8 | 2.8 × 10−9 |
| HOI | 2.5 | 3.2 × 10−11 |
Note that the influence of central atom electronegativity on the strength of oxyacids is exactly the opposite to that observed for the binary hydrides in Table \(\PageIndex{5}\), for which the acidity increased down a group, giving the order of acidity:
\[\ce{HI>HBr>HCl \gg HF} \nonumber \]
The reason for this is that in the hydrogen halides, the bond to be broken (H-E bond) decreased in strength down the group, while in oxyacids the bond to be broken is always an O-H bond and so varies much less in strength with the electronegativity of the central atom.
Trend 2: For oxoacids of a given central atom the acidity increases with the central element's oxidation state or, in other words, the number of oxygens bound to the central atom.
Here we are looking at the trend for acids in which there are variable numbers of oxygen bound to a given central atom. An examples is the perchloric (\(\ce{ClO_4^{-}}\)), chloric (\(\ce{ClO_3^{-}}\)), chlorous (\(\ce{ClO_2^{-}}\)), and hypochlous (\(\ce{ClO^{-}}\)) acid series. In such a series, the greater the number of oxygens, the stronger the acid. This can be explained in several ways. From the viewpoint of the acid itself the key factor is again the inductive effect, in this case involving the ability of the oxygens attached to the central atom to pull on electron density across the OH bond. This is seen from the charge density diagram for the chlorine oxoacids shown in Figure \(\PageIndex{1}\), in which the partial positive charge on the acidic hydrogen increases with the number of oxygens present.
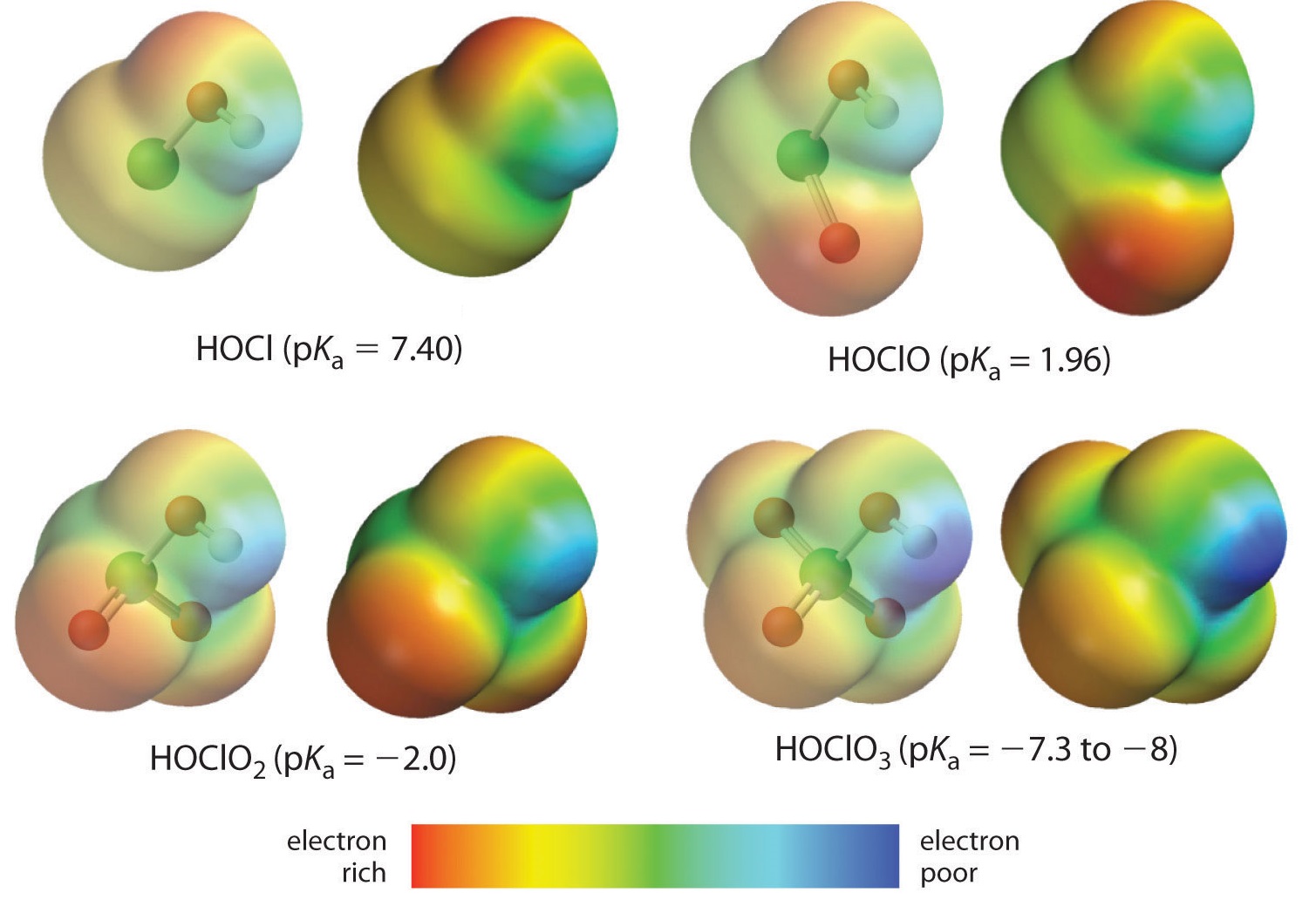
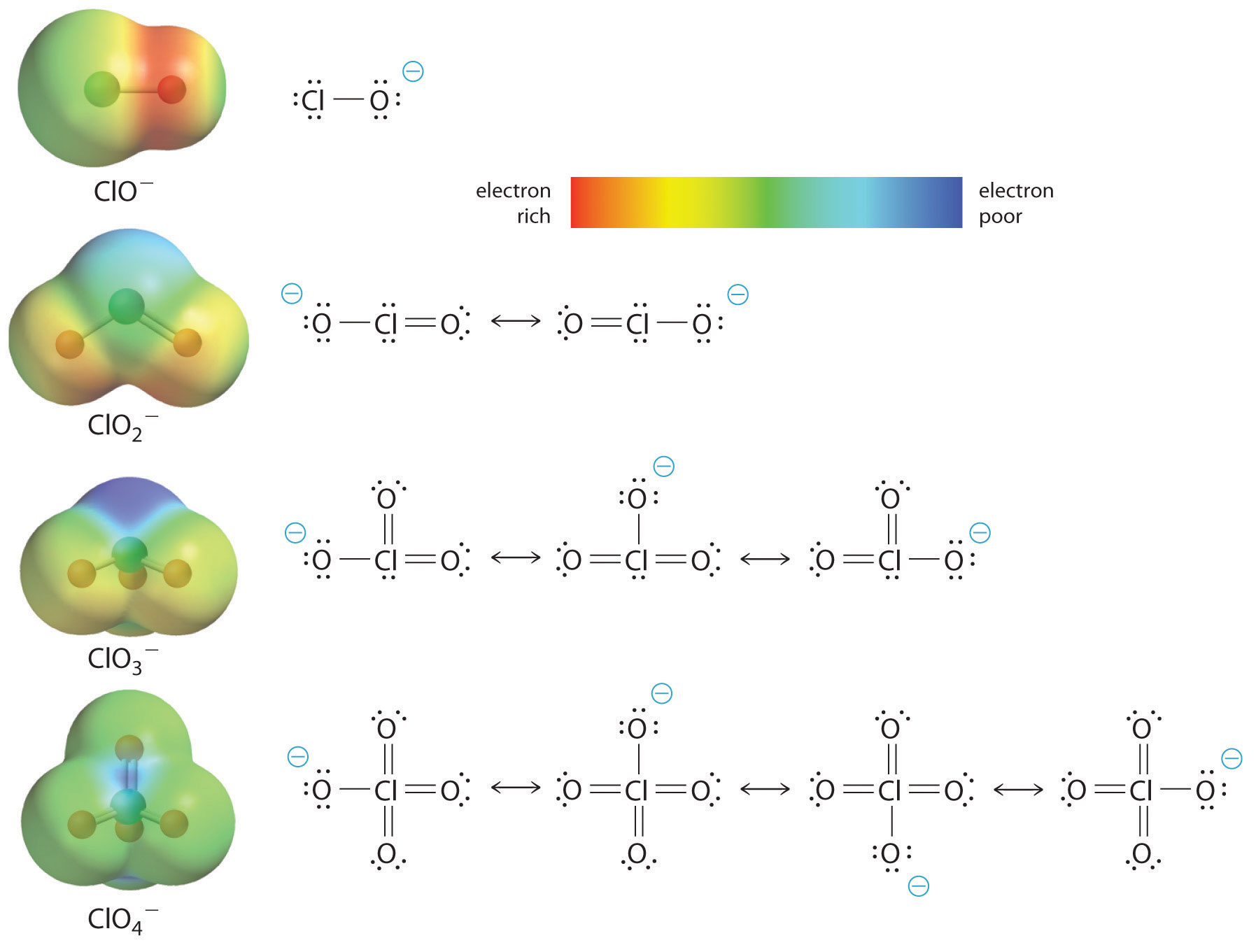
The increase in oxoacid acidity with the number of oxygens bound to the central atom may also be seen by considering the stability of the conjugate oxyanion. That the stability of the conjugate base increases with the number of oxygens may be seen from the charge distribution diagrams and Lewis bonding models for the chlorine oxyanions shown in figure \(\PageIndex{2}\) . As the negative charge is spread over more oxygen atoms it becomes increasingly diffuse.
Sulfur and selenium both forms oxoacids of formula \(\ce{H_2EO_3}\), where E is either S or Se. These are called sulfurous and selenous acid, respectively. Which oxoacid would you expect to be more acidic: selenous acid or sulfurous acid?
- Answer
-
Sulfurous acid should be more acidic. Since sulfur is more electronegative than selenium sulfur will polarize OH bonds to a greater extent, making them more acidic. This prediction is borne out by a comparison of the \(pK_a\) values for the acids:
Acid \(pK_{a1}\) \(pK_{a2}\) sulfurous acid, \(H_2SO_3\) 1.85 7.2 selenous acid, \(H_2SeO_3\) 2.62 8.32
Trend 3: For polyprotic oxoacids the acidity decreases as each successive proton is removed
Oxoacids with multiple O-H bonds are called polyprotic since they can donate more than one hydrogen ion. In this case hydrogen ions are removed in successive ionization reactions. Examples include phosphoric and carbonic acid:
\[\ce{H_3PO_4 ⇌ H^{+} + H_2PO_4^{-}} \quad \quad pK_{a1} = 2.2 \nonumber \]
\[\ce{H_2PO_4^{-} ⇌ H^{+} + HPO_4^{2-}} \quad \quad pK_{a2} = 7.2 \nonumber \]
\[\ce{HPO_4 ⇌ H^{+} + PO_4^{3-}} \quad \quad pK_{a3} = 12.4 \nonumber \]
\[\ce{H_2CO_3 ⇌ H^{+} + HCO_3^{-}} \quad \quad pK_{a1} = 3.6 \nonumber \]
\[\ce{HCO_3^{-} ⇌ H^{+} + CO_3^{2-}} \quad \quad pK_{a1} = 10.3 \nonumber \]
The dissociation constants for successive ionization constants decrease by about five orders of magnitude between successive hydrogen ions. This is reflected in Linus Pauling's rules for oxoacids and their oxyanions:
- The \(pK_a\) for an oxyacid of general formula \(\ce{E(OH)_{q}(O)_{p}}\) is given by \[pK_a = 8 - 5 \times p \label{PaulingRules} \]
- As an oxoaxid undergoes successive ionizations the \(pK_a\) increases by five each time.
The central theme of Pauling's Rules is that the more oxygens there are on the central atom, the more resonance structures that can be constructed for the conjugate base, which increases its stability and increases the acidity of the acid. However, as the acids successively ionize, they have fewer resonance structures. Pauling's Rules are phenomenological (i.e., not based on a theoretical framework). However, as empirical rules, they often work quite well, but it should be borne in mind that they are approximate.
Calculate the theoretical \(pK_a\) values for phosphoric and carbonic acid and their dissociation produces and compare the results with the experimental \(pK_a\) values.
- Answer
-
For phosphoric acid, Pauling's rules (Equation \ref{PaulingRules}) predict the \(pK_a\) values quite well:
- \(H_3PO_4\): \(p = 3\) and \(q =1\) and \[pK_{a1, predicted} = 8 - 5 \times 1 = 3 \nonumber \] This is slightly greater than the observed value of 2.2.
- \(H_2PO_4^-\): \[pK_{a2, predicted} = pK_{a1, experimental} + 5 = 7.2 \nonumber \] This is spot on with experiment.
- \(HPO_4^{2-}\): \[pK_{a3, predicted} = pK_{a2, experimental} + 5 = 12.2 \nonumber \] This is slightly less than the experimental value of 12.4.
For carbonic acid Pauling's rules predict \(pK_{a1}\) reasonably well, but \(pK_{a2}\) less so:
- \(H_2CO_3\): \(p = 2\), \(q =1\) and \[pK_{a1, predicted} = 8 - 5 \times 1 = 3 \nonumber \] This is slightly lower than the observed value of 3.6.
- \(HCO_3^-\): \[pK_{a2, predicted} = pK_{a1, experimental} + 5 = 8.6 \nonumber \] This is 1.7 units less than the experimental value of 10.3.
In some cases discrepancies between experimental \(pK_a\) values and those predicted by Pauling's rules suggest that structural rearrangements may be taking place upon ionization or else that the reported \(pK_a\) values do not really represent the ionization in question because they do not fully account for all the equilibria taking place in solution. In the case of carbonic acid, however, the reason for the discrepancy between the predicted and experimental \(pK_{a2}\) values is not entirely clear.


