19.13: Mass-Energy Relationships

In a nucleus the protons and the neutrons are held very tightly by forces whose nature is still imperfectly understood. When the nucleons are very close to each other, these "nuclear forces" are strong enough to counteract the Coulombic repulsion of the protons, but they fall off very rapidly with distance and are essentially undetectable outside the nucleus. Because the energies involved in binding the nucleons together are very large, they give rise to an effect which makes it possible to measure them. According to Einstein’s special theory of relativity, when the energy of a body increases, so does its mass, and vice versa. If the change in energy is indicated by ΔE and the change in mass by Δm, these two quantities are related by the equation

\[{\Delta\text{E}} = {\Delta\text{mc}}^2\label{1} \]

where c is the velocity of light (2.998 × 10⁸ m s^–1).

In ordinary chemical reactions this change in mass with energy is so small as to be undetectable, but in nuclear reactions we invariably find that products and reactants have different masses. As a simple example, let us take the dissociation of a deuteron into a proton and a neutron:

\[{}_{\text{1}}^{\text{2}}\text{D }\to \text{ }{}_{\text{1}}^{\text{1}}p\text{ + }{}_{\text{0}}^{\text{1}}n \nonumber \]

The molar mass of a deuteron is found experimentally to be 2.013 55 g mol^–1 (Table \(\PageIndex{1}\)), but if we add the molar masses of a neutron and a proton, we obtain a somewhat higher value, namely, (1.007 28 + 1.008 67) g mol^–1 = 2.015 95 g mol^–1. The change in mass using the usual delta convention is thus (2.015 95 – 2.013 55) g mol^–1 = 0.002 40 g mol^–1. From Eq. \(\ref{1}\) we then have

\[{\Delta\text{E}} = {\Delta\text{mc}}^2 = 0.002 40 \frac{\text{g}}{\text{mol}}\text{ }\times \text{ }\frac{\text{1 kg}}{\text{10}^{\text{3}}\text{ g}} \times \left(2.998 \times {\text{10}^{\text{8}}\frac{\text{m}}{\text{s}}} \right)^2 \nonumber \]

= 2.16 × 10¹¹ kg m² s^–2 mol^–1 = 216 × 10⁹ J mol^–1 = 216 GJ mol^–1

Table \(\PageIndex{1}\):The Molar Masses of Some Selected Nuclei (Electrons Are Not Included in These Masses).

Nucleus	M/g mol^–1	Nucleus	M/g mol^–1
\({}_{\text{0}}^{\text{1}}n\) (neutron)	1.008 67	\({}_{\text{26}}^{\text{56}}\text{Fe}\)	55.920 66
\({}_{\text{1}}^{\text{1}}p\) (proton)	1.007 28	\({}_{\text{27}}^{\text{59}}\text{Co}\)	58.918 37
\({}_{\text{1}}^{\text{2}}\text{D}\) (deuteron)	2.013 55	\({}_{\text{36}}^{\text{84}}\text{Kr}\)	83.8917
\({}_{\text{1}}^{\text{3}}\text{T}\) (tritium)	3.015 50	\({}_{\text{50}}^{\text{120}}\text{Sn}\)	119.8747
\({}_{\text{2}}^{\text{4}}\text{He}\)	4.001 50	\({}_{\text{56}}^{\text{138}}\text{Ba}\)	137.8743
\({}_{\text{3}}^{\text{7}}\text{Li}\)	7.014 36	\({}_{\text{78}}^{\text{194}}\text{Pt}\)	193.9200
\({}_{\text{6}}^{\text{12}}\text{C}\)	11.996 71	\({}_{\text{83}}^{\text{209}}\text{Bi}\)	208.9348
\({}_{\text{8}}^{\text{15}}\text{O}\)	14.998 68	\({}_{\text{92}}^{\text{235}}\text{U}\)	234.9934
\({}_{\text{8}}^{\text{16}}\text{O}\)	15.990 52	\({}_{\text{94}}^{\text{239}}\text{Pu}\)	239.0006
\({}_{\text{8}}^{\text{17}}\text{O}\)	16.994 74

Since expansion work or even electronic energies are negligible compared to this change in nuclear energy, we can equate the change in nuclear energy either to the change in internal energy or the enthalpy; that is,

ΔE = ΔU_m = ΔH_m = 216 GJ mol^–1

The energy needed to separate a nucleus into its constituent nucleons is called its binding energy. The binding energy of the 21H nucleus is thus 216 GJ mol^–1. Notice how very much larger this is than the bond energy of an average molecule, which is about 200 or 300 kJ mol^–1. Since a gigajoule is 1 million kJ, the energies involved in holding the nucleons together in a nucleus are something like a million times larger than those holding the atoms together in a molecule.

Since the number of nucleons in a nucleus is quite variable, it is useful to calculate the average energy of each nucleon by dividing the total binding energy by the number of nucleons, A. This gives the binding energy per nucleon. In the case of the nucleus 5626Fe, for instance, we can easily find from Table \(\PageIndex{1}\) that Δm for the process

\[{}_{\text{26}}^{\text{56}}\text{Fe }\to \text{ 26}{}_{\text{1}}^{\text{1}}p\text{ + 30}{}_{\text{0}}^{\text{1}}n \nonumber \]

has the value 0.528 72 g mol^–1, giving a value for ΔH_m, from Eq. (19.35)of 4750 GJ mol^–1. Since A = 56 for this nucleus, the binding energy per nucleon has the value

\[\frac{\Delta H_{m}}{A} = \frac{\text{4750}}{\text{56}} \nonumber \] GJ mol^–1 = 848 GJ mol^–1

The binding energy of a nucleus tells us not only how much energy must be expended in pulling the nuclei apart but also how much energy is released when the nucleus is formed from protons and neutrons. In the case of the 5626Fe, for instance, we have

\[\text{26}{}_{\text{1}}^{\text{1}}p\text{ + 30}{}_{\text{0}}^{\text{1}}n\text{ }\to \text{ }{}_{\text{26}}^{\text{56}}\text{Fe} \nonumber \]

ΔH_m = –4.75 × 10³ GJ mol^–1 

that is, the energy of formation of 5626Fe is equal to the negative of the binding energy. In Figure \(\PageIndex{1}\) the energy of formation on a per nucleon basis has been against the mass number for the most stable isotope of each element. The zero energy axis in this plot corresponds to the energy of completely separated protons and neutrons, while the points on the graph correspond to the average energy of a nucleon in the nucleus in question. Obviously, the lower the energy, the more stable the nucleus.

As we can see from Figure \(\PageIndex{1}\), the most stable nuclei are those of mass number close to 60, the nucleus with the lowest energy being the5626Fe nucleus. As the mass number rises above 60, the nuclei become slightly higher in energy, i.e., less stable. Decreasing the mass number below 60 also brings us into a region of high-energy nuclei. With the exception of the 42He, nucleus, the nuclei of highest energy belong to the very lightest elements.  

Figure \(\PageIndex{1}\): Energy of formation per nucleon (from protons and neutrons) as a function of mass number.

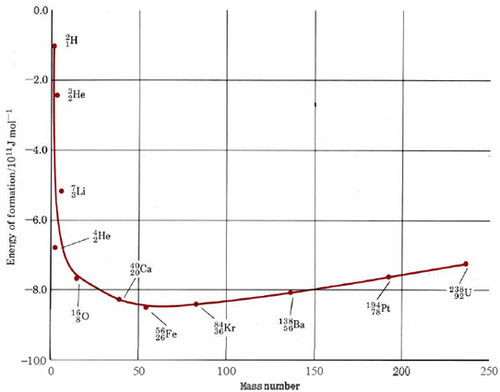
Figure \(\PageIndex{1}\) shows us that in principle there are two ways in which we can obtain energy from the nuclei of the elements. The first of these is by the splitting up or fission of a very heavy nucleus into two lighter nuclei. In such a case each nucleon will move from a situation of higher to lower energy and energy will be released. Even more energy will be released by the fusion of two very light nuclei, each containing only a few nucleons, into a single heavier nucleus. Though fine in principle, neither of these methods of obtaining energy is easy to achieve in practice in a controlled way with due respect to the environment.