15.5: Thermodynamic Terms and Conventions
- Page ID
- 49532
We define the internal energy in molecular terms in another section, but it is important to realize that we can deal with this property purely in macroscopic terms as well. Thus we can talk about the internal energy of a substance without even knowing its chemical formula. More importantly, we can usually measure the change in the internal energy which accompanies a physical or chemical change without having the slightest idea of what is happening on the molecular level. In order to show how this is done, we first need to introduce the following conventions and terms:
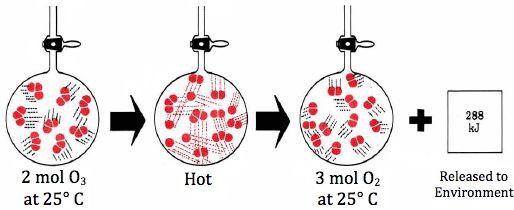
1 System. The term system is used to describe any sample of matter in which we are particularly interested. Thus, in the conversion of O3 to O2 described in Figure \(\PageIndex{1}\), the system would denote the contents of the flask before, after, or during the chemical change which occurs. Initially the system would thus consist of 2 mol O3 and finally of 3 mol O2.
2 Initial and final states. In thermodynamics our principal concern is with the initial state before any changes begin, and the final state, when no more changes occur. By convention we refer to the initial state with the subscript 1 and to the final state with the subscript 2. Referring again to the reaction illustrated in Figure \(\PageIndex{1}\), if the volume of the flask is 24.47 dm³, the initial pressure P1 will be 202.7 kPa (2.00 atm) and the final pressure P2 will be 304.0 kPa (3.00 atm). Likewise we could refer to the initial value of the internal energy as U1 and the final value as U2. 3 The delta convention. When a chemical or physical change occurs, many of the properties of the system change. We conventionally refer to a change in a property with the symbol Δ (delta). In the O3–O2 reaction, for example, the pressure P increases by 101.3 kPa, and we can indicate this fact by writing
-
- \[\triangle P = 101.3 \text{kPa} \nonumber \]
More formally, if a property X changes from an initial value X1 to a final value X2, then ΔX is defined as
-
- \[\triangle X = X_{2} – X_{1} \nonumber \]
Thus, in the above case.
-
- \[\triangle P = P_{2} – P_{1} = 304.0 \text{kPa} – 202.7 \text{kPa} = 101.3 \nonumber \]
We can also describe changes in internal energy using the delta convention. It is apparent from Table 1 in Internal Energy that the conversion of 2 mol O3 to 3 mol O2 results in a decrease of 287.9 kJ in the internal energy. In the delta convention we express this as a negative quantity:
-
- \[\triangle U = U_{2} – U_{1} = –287.9 \text{kJ} \nonumber \]
since the initial value of U is larger than the final value. 4 Heat energy. Our final convention refers to the heat energy q absorbed by the system. If the heat change occurs at constant volume, the symbol qV is used, if at constant pressure, qp. By convention we refer to the heat energy absorbed by the system as being positive and the heat energy released by the system as being negative. In the O3 to O2 conversion described in Figure \(\PageIndex{1}\), for example, we would write
-
- \[q_{V} = –287.9 \text{kJ} \nonumber \]
since the system releases 287.9 kJ of heat energy to the surroundings. Now that we are familiar with these conventions, we can use them to state an important general principle. When a chemical or physical change occurs at constant volume, the heat energy absorbed by the system is equal to the increase in its internal energy, or in mathematical language
-
- \[q_{V} = \triangle U \nonumber \]
This general behavior of matter is an immediate consequence of the law of conservation of energy. If an endothermic reaction occurs at constant volume and heat energy is absorbed by the reaction system, then this heat energy cannot disappear: It all goes toward increasing U. Alternatively, if the internal energy decreases, as in Figure \(\PageIndex{1}\), no energy is lost: It all appears as heat energy and is transferred to the surroundings.