19.1: Micelle Formation

In particular, we will focus on micellar structures formed from a single species of amphiphilic molecule in aqueous solution. These are typically lipids or surfactants that have a charged or polar head group linked to one or more long hydrocarbon chains.

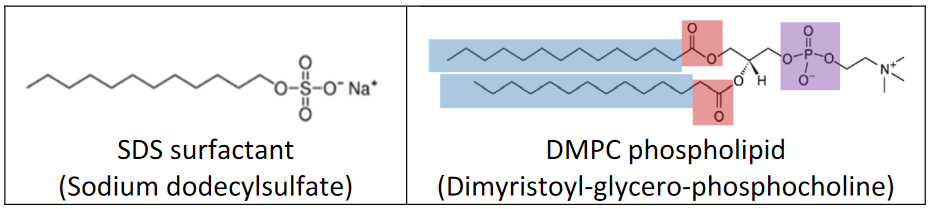
Such amphiphiles assemble into a variety of structures, the result of which depends critically on the concentration, composition, and temperature of the system. For SDS surfactant, micelles are favored. These condense hydrophobic chains into a fluid like core and present the charged head groups to the water. The formation of micelles is observed above a critical micelle concentration (CMC).

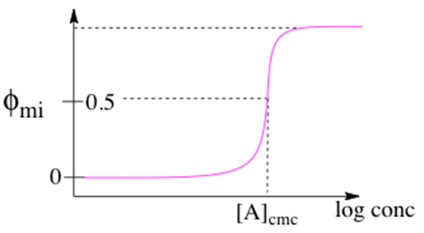
As the surfactant is dissolved, the solution is primarily monomeric at low concentration, but micelles involving 30–100 molecules suddenly appear for concentrations greater than the CMC.

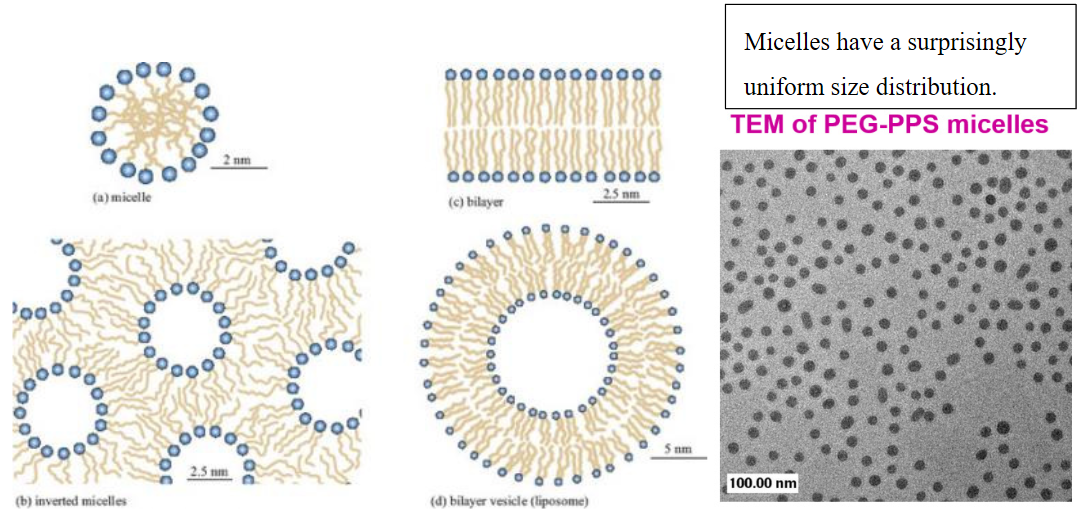
Reprinted from http://swartz-lab.epfl.ch/page-20594-en.html.

To begin investigating this phenomenon, we can start by simplifying the equilibrium to a two-state form:

\[ nA \rightleftharpoons A_n \]

\(K_n\) is the equilibrium constant for assembling a micelle with \(n\) amphiphiles from solution. \(n\) is the called the aggregation number.

\[K_n = \dfrac{[A_n]}{[A]^n} = e^{-\Delta G^0_micelle / k_BT} \label{1}\]

The total number of \(A\) molecules present is the sum of the free monomers and those monomers present in micelles:

\[CTOT = [A] + n[A_n].\]

The fraction of monomers present in micelles:

\[ \phi_mi = \dfrac{n[A_n]}{C_{TOT}} = \dfrac{n[A_n]}{[A]+n[A_n]} = \dfrac{nK_n[A]^{n-1}}{1+nK_n[A]^{n-1}} \]

This function has an inflection point at the CMC, for which the steepness of the transition increases with \(n\). Setting \(φ_{mi} = 0.5\), we obtain the CMC (\(c_0\)) as

\[ c_0 = [A]_{cmc} = (nK_n)^{\dfrac{-1}{n-1}} \]

Function steepens with aggregation number \(n\):

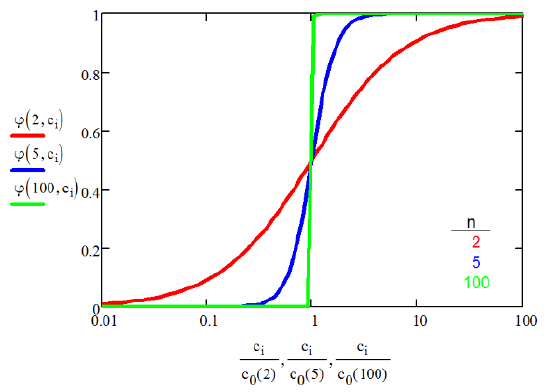
Thus for large n, and cooperative micelle formation:

\[ \Delta G^0_{micelle} = -RT\ln{c_0} \]

Note the similarity of Equation \ref{1} to the results for fractional helicity in the helix-coil transition:

\[ \dfrac{s^n}{1+s^n}\]

This similarity indicates that a cooperative model exists for micelle formation in which the aggregation number reflects the number of cooperative units in the process. Cooperativity can be obtained from models that require surmounting a high nucleation barrier before rapidly adding many more molecules to reach the micelle composition.The simplest description of such a process would proceed in a step-wise growth form (a zipper model) for \(n\) copies of monomer \(A\) assembling into a single micelle \(A_n\).

\[ nA \rightleftharpoons A_2 +(n+2)A \rightleftharpoons A_3 +(n-3)A \rightleftharpoons ... \rightleftharpoons A_n \]

\[ K_n = \prod_{i=1}^{n-1} K_i \qquad K_i = \dfrac{k_f(i \rightarrow i+1}{k_r(i+1 \rightarrow i} \]

Examples of how the energy landscape looks as a function of oligomerization number ν are shown below. However, if you remove the short-range correlation, overall we expect the shape of the energy landscape to still be two-state depending on the nucleation mechanism.

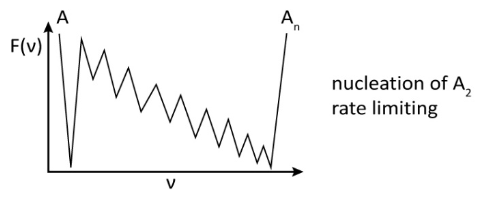
This picture is overly simple though, since it is not a one-dimensional chain problem. Rather, we expect that there are equilibira connecting all possible aggregation number clusters to form larger aggregates. A more appropriate description of the free energy barrier for nucleating a micelle is similar to classical nucleation theory for forming a liquid droplet from vapor.

____________________________________________________________

D. H. Boal, Mechanics of the Cell, 2nd ed. (Cambridge University Press, Cambridge, UK, 2012), p. 250.