A5. Transition State Stabilization
- Page ID
- 132870
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
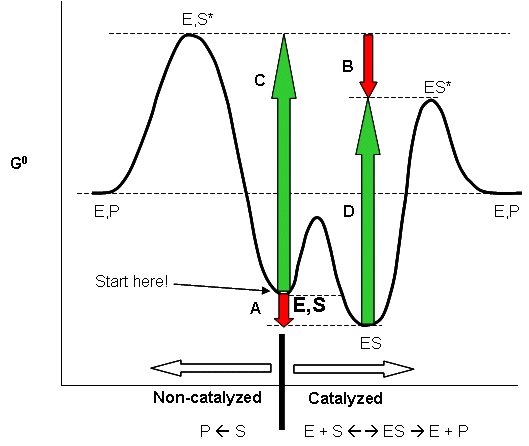
Linus Pauling postulated long ago that the only thing that a catalyst must do is bind the transition state more tightly than the substrate. That this must be the case can be seen from the diagram below, which shows how \(S\) and \(S*\) (the transition state) can react with E to form a complex which then proceeds to product, or can go to product in the absence of \(E\). From this diagram, it should be evident that \(c - a = d -b\), where \(a\) is the \(\Delta G^o\) for the binding of \(S\) to \(E\), and \(b\) is the \(\Delta G^o\) for the binding of S* to E. For an enzyme to be a catalyst the activation energy for the reaction in the presence of \(E\), \(d\), must be less than in the absence of enzyme, \(c\). Therefore \(c-d = a-b > 0\). Since \(\Delta G^o = -RT\,\ln\, K_{eq}\), \(K_{eq}\) for binding of \(S*\) to \(E\) is greater than for \(S\) binding to \(E\).
Figure: ENZYMES BIND THE TRANSITION STATE MORE TIGHTLY THAN THE SUBSTRATE
The stability of the transition state also affects the reaction kinetics (which makes sense given that the activation energy clearly affects the speed of a reaction). As you probably remember from organic chemistry, SN2 reactions are slow when the central atom where the substitution will occur is surrounded by bulky substitutents (sterics once again). We discussed this in context to nucleophiliic substitution on a sp2 hybridized carbonyl carbon in carboxylic acid derivatives versus on a sp3 hybridized phosphorous in phosphoesters and diesters.; The explanation for this phenomena has usually been attributed to hindered access of the central atom caused by bulky substituents (intrinsic effects). Is this true?; Recent studies on SN2 reactions of methylchloroacetonitrile and t-butylchloroacetonitrile (with the reagent labeled with 35Cl) using 37Cl- as the incoming nucleophile in the gas phase shown that the more hindered t-butyl derivative's activation energy was only 1.6 kcal/mol higher than the methyl derivative, but in aqueous solution, the difference is much greater for comparable reactions. They attributed the differences to solvation effects of the transition state. The bulkier the substituents on the central atom, the more difficult it is to solvate the transition state since water can't reorient around it as well. In effect there is steric hindrance for both reactant and solvent.
Abyzmes - Antibody Catalysis
What does it take for a macromolecule (M) to be a catalyst - an enzyme. It seems the minimum criterion are:
- M binds a reactant
- M binds the transition state more tightly than the substrate
Anything above these is just "icing on the cake". If different functional group are present in the "active" site of the enzyme that would allow electrostatic, intramolecular, covalent, general acid and/or base catalysis, the better the catalyst.
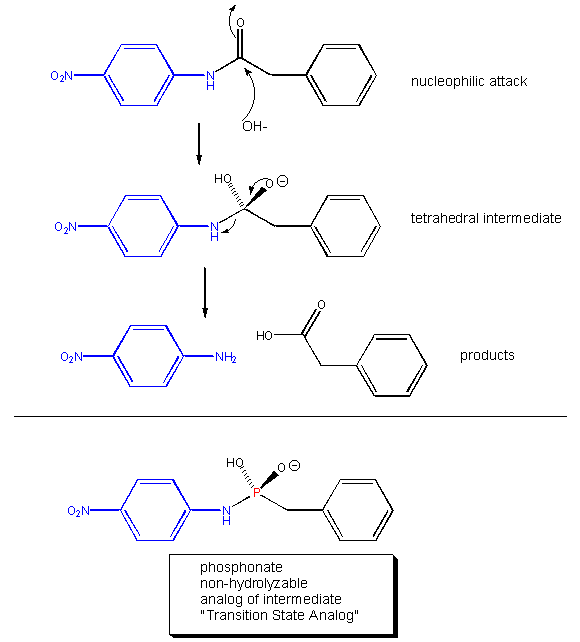
Linus Pauling recognized the two key factors decades ago. He made the following hypothesis: Antibody molecules (immune system proteins that bind foreign molecules) that can be made to bind to transition state analogs of a substrate, should also presumably catalyze the conversion of substrate, through the transition state, to product. About a decade ago, his prediction was verified. Lerner et al. made a transition state analog of an ester. When an ester is hydrolyzed, the sp2 hybridized carbonyl carbon is converted to an sp3 hybridized center in the intermediate, with the carbonyl oxygen becoming an oxyanion. The transition state presumably looks more like this unstable intermediate (sp3, oxyanion). Lerner synthesized a phosphonate, an ester mimic with a sp3 hybridized phosphorous replacing the carbonyl C. It also has a negatively charged oxygen as does the intermediate for the ester. This phosphonate ester is very resistant to hydrolysis. When injected into a mouse (after first being covalently attached to a carrier protein so the small molecule becomes "immunogencic"), the mouse makes a protein antibody which binds to the phosphonate. When the corresponding carboxylic acid ester is added to the antibody, it is cleaved with nominal kcat and Km values. Site specific mutagenesis can then be done to make it an even better catalyst! The antibody enzymes have been called abzymes. The structure below shows how phosphonamides act as transition state analogs as well.
Figure: PHOSPHONAMIDES: TRANSITION STATE ANALOGS
![]() Jmol: Updated Immunoglobulin 48G7 Germline Fab Antibody Complexed With Hapten 5-(Para-Nitrophenyl Phosphonate)-Pentanoic Acid Jmol14 (Java) | JSMol (HTML5)
Jmol: Updated Immunoglobulin 48G7 Germline Fab Antibody Complexed With Hapten 5-(Para-Nitrophenyl Phosphonate)-Pentanoic Acid Jmol14 (Java) | JSMol (HTML5)
Transition state theory can be used to more clearly quantify the relationships described in the graphical analysis above. This analysis will use the equilibrium constant (in contrast to the last two chapters which used dissociation constants to characterize macromolecule, receptor, and enzyme binding to ligand). Let assume that a substrate S is in equilibrium with its transition state S‡. Hence Keq = [S‡]/[S]. The following reaction can be written: S --> S‡ --> P. Based on our previous kinetic analysis and experience in writing differential equations, dP/dt = k1[S‡]. By analogy, enzyme bound S (ES) can be converted to (ES‡) and then on to product as shown in the following chemical equation:
E + S <----> ES --> ES‡ --> E + P.
For the non-enzyme catalyzed reaction, transition state theory can be used to show that the first order rate constant k1= kT/h where k is the Boltzman's constant, T is the Kelvin temperature, and h is Planck's constant. Hence, using Keq = [S‡]/[S], equation 1 can be derived
1.
where kn (hereafter written as kN) =(kT/h)K‡ is the effective first order rate for the non-catalyzed rate. Now lets create a more complicated linked equilibrium showing the same reaction in the presence of an enzyme.
Remember that the K values for this analysis are equilibrium constants not dissociation constants. Note two important equilibrium constants, KS, the equilibrium constant for the binding of free S to E, and KT, the equilibrium constant for the binding of free S‡ to E (assuming that free S‡ could bind to E before it converted to product). As we have seen for linked equilibrium before, since the Keq values are related to the standard free energy changes which are state functions, the sum of the standard free energies going from E + S to ES‡ (by either the top or bottom paths) are path independent so the products of the Keq for the top path are equal to those for the bottom paths. This gives the following equation:
2.
The right hand side is the ratio of the effective first order rate constant for conversion or ES‡ --> E + P, kE dvided by the rate constant for the conversion of S‡ --> P for the noncatalyzed rate, kN. The final ratio of rate constants can be derived from the simple relationship that kx=(kT/h)K‡x where x is either N (non catalyzed) or E (enzyme catalyzed). Equation 2 states that the equilibrium constant for the binding of S‡ to E, KT, is greater than the equilibrium constant for the binding of S to E, KS (as kE > kN). KT/KR ranges from 108 - 1014. Given common values for the equilibrium constant for binding of S to E (103 - 105 M-1) which is equivalent to dissociation constant values Kd = 10 uM -1 mM, the calculated value of KT = 1015 M-1 which gives a dissociation constant for the enzyme and transition state of Kd = 10-15 M (1 femtomolar). This is as tight as one of the highest affinity binding interactions in the biological world, the binding of avidin and biotin. As we noted in Chapter 5A, assuming that the second order rate constant for avidin/biotin binding and as shown above for E/S‡ is diffusion controlled (about 108 M-1s-1), the off rate for the avidin-biotin or ES‡complex is 10-7 s-1, equivalent to a half life of the complex of 80 days. It doesn't get much tighter than that.
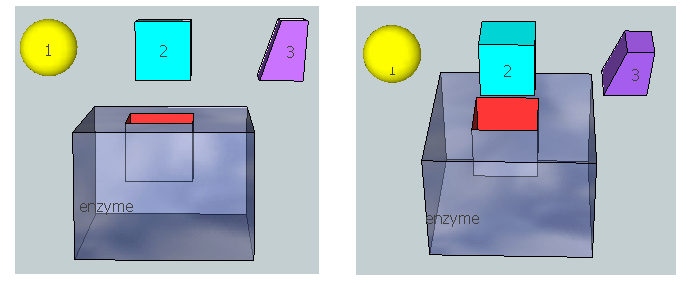
The figure below represent an image of an enzyme and three different molecules, 1-3, that could bind to it. Using the analysis above, which molecule do you think represents substrate? Transition state? Product?
Figure: 3D model for binding substrate, transition state, and product to an enzyme
Animated Version