Chemical Equilibrium (Strein)

Solution Example Problem 1

1) A solution is prepared by dissolving 10.00 ± 0.02 g of K₂SO₄ into distilled water and that solution is diluted to the mark in a 100.00 mL volumetric flask.

Using the rules for significant figures, and the rules for propagation of uncertainty, calculate:

1. The Formality of K₂SO₄
2. The % by weight of K₂SO₄
   (solution density is 1.075 ± 0.003 g/mL)
3. The molality of K₂SO₄

…Which method is superior?

Solution Example Problems 2,3

2) What volume of 0.573 F K₂SO₄ would be needed to prepare 1.00 L of 5.00x10^-3 F K₂SO₄ ?

3) Assuming the 5.00x10^-3 F K₂SO₄ solution above has a density of 1.000 g/mL, calculate the concentration of K⁺ ions in units of ppm.

Average and Uncertainty

Triplicate measurements (maybe densities, for example…):

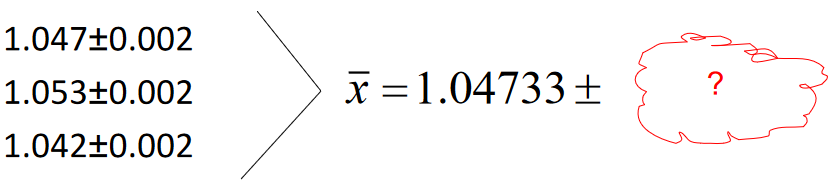
Calculate the average and the associated uncertainty.

Consider A Strong Acid HCl

(what is the pH?)

Concentration of HCl (F HCl = M H^+)	pH = - log([H^+])
1.00x10^-1 F	1.000
1.00x10^-2 F	2.000
1.00x10^-3 F	3.000
1.00x10^-4 F	4.000
1.00x10^-5 F	5.000
1.00x10^-6F	6.000
1.00x10^-7 F	7.000
1.00x10^-8 F	8.000  ????!!!!????

Strong Acids: The Systematic Approach

(multiple equations, as many unknowns)

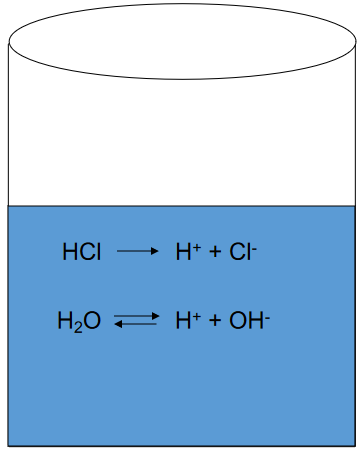
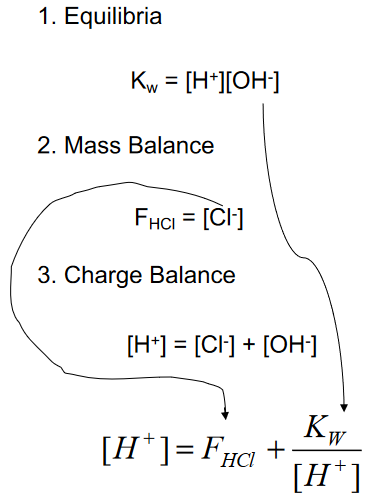
Consider A Strong Acid HCl

(what is the pH with QUAD?)

Concentration of HCl	pH
1.00x10^-1 F	1.000
1.00x10^-2 F	2.000
1.00x10^-3 F	3.000
1.00x10^-4 F	4.000
1.00x10^-5 F	5.000
1.00x10^-6 F	5.996
1.00x10^-7 F	6.790
1.00x10^-8 F	6.976

Example WA problem

Calculate the pH of a solution that is 0.100 F acetic acid (K_a = 1.75 x 10^-5).

Use the “ICE” method to start.

What assumption(s) can be made to make this simple?

Example WB problem

Calculate the pH of a solution that is 0.100 F NH₃ (must calculate K_b, given K_a of NH₄⁺ ).

Use the “ICE” method to start.

What assumption(s) can be made to make this simple?

Example mixture problems

(no buffers yet)

1. Calculate the pH of a solution prepared by mixing 10.00 mL of 0.100 F acetic acid and 10.00 mL of deionized water.
2. Calculate the pH of a solution prepared by mixing 10.00 mL of 0.100 F acetic acid and 10.00 mL of 0.100 F NaOH.
3. Calculate the pH of a solution prepared by mixing 10.00 mL of 0.100 F acetic acid and 10.00 mL of 0.200 F NaOH.

Buffer Example problems

1. Calculate the pH of a solution prepared by dissolving 0.100 mole of acetic acid and 0.150 mole of sodium acetate into the same 1.00 L solution.
2. Calculate the pH of a mixture of 30.00 mL of 0.150 F HNO₂ and 20.00 mL of 0.180 F NaNO₂.
3. Calculate the pH of a mixture of 20.0 mL of 0.112 F HNO₂ and 10.00 mL of 0.100 NaOH.
4. Calculate the pH of 20.0 mL of 0.012 F HNO₂ and 15.0 mL of 0.010 F NaOH.

“Backwards” Buffer Problem

You are asked to make 1.00 L of buffer solution at pH 4.315. You are given a solution of 0.100 F acetic acid and a solution of 0.500 F NaOH. How much of each solution do you need?

A Titration of HA with OH^-

Consider the titration of 50.00 mL of 0.100 F Acetic Acid with 0.100 F NaOH. Construct the shape of the titration curve by calculating the pH at various volumes.

Note the pH on the buffer region, at the end point, and on the “final” plateau and generalize these values.

Polyprotic Example Problems

1. Calculate the pH of 0.0600 F Oxalic Acid, H₂(COO)₂.
2. Calculate the pH of a 0.0500 F solution of sodium oxalate, Na₂(COO)₂.
3. Calculate the pH of a 0.0500 F solution of monosodium oxalate.

Polyprotic Mixing Problems

(Polyprotics react more than once!)

Calculate the pH of a mixture of 30.00 mL of 0.100 F phosphoric acid with 9.68 mL of 0.500 F NaOH.

“Backwards” Buffer Problems with Polyprotics

(Polyprotics react more than once!)

How many mL of 0.100 F NaOH would you need to add to 100.00 mL of 5.00x10^-2 F phthalic acid to result in a buffer at pH 5.00?

Composition Example Problem

Calculate the fraction of each acid/base form of carbonate at pH= 5.00.

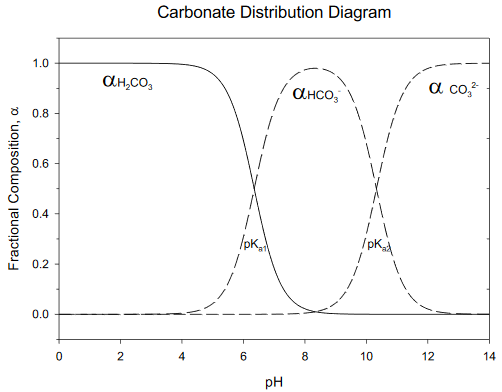
Solubility Calcs

(ignoring side reactions)

1. Calculate the solubility of PbI₂ in pure water.
2. Using the ion product, predict if a precipitate will form when equal volumes of 0.0100 F Pb(NO₃)₂ and 0.100 F KI are mixed.

Common Ion Example

Calculate the solubility of Ba(IO₃)₂ in

1. pure water
2. 0.0200 F KIO₃
3. 0.00200 F KIO₃

pH effect on S

Calculate the solubility of calcium carbonate in:

1. Pure water (ignoring side reactions)
2. A sol’n that is held at pH = 7.00
3. A sol’n that is held at pH = 11.00

Consider S at pH 3.00 …. S = 17 M !? What’s wrong?

Combining common ion and pH effect

Calculate the solubility of silver iodate in 0.010 F KIO₃ at pH = 2.00.

Fractional Precipitation

Consider a solution that contains 0.100 M IO₃^- and 0.100 M SO₄^2- (and 0.300 M Na⁺). If a solution of 0.100 F Ba(NO₃)₂ is added, dropwise, what will happen?

Can we quantitatively (99.9%) remove all of the sulfate without removing any of the iodate?

Precipitation Titration

Consider the titration of 10.00 mL of 0.100 F NaCl with 0.100 F AgNO₃.

Calculate pAG throughout the range from 0.00 to 20.00 mL.

(what volume is the V_eq ?).

Cl^- as a ligand for Cd²⁺

Chloride forms a mono- , di- , and tri-chloride complex with Cd²⁺

Stepwise formation constants:

K_f1 =10^1.5        K_f2 =10^0.4        K_f3  = 10^0.4

Derive the fraction of free Cd²⁺ in a solution that contains chloride (α_Cd2+).

\[\begin{align}
\alpha_{Cd^{2+}} &= (1 + K_{f1}[Cl^-] + K_{f1}K_{f2} [Cl^-]^2  + K_{f1}K_{f2} K_{f3}[Cl^-]^3 )^{-1}\nonumber\\
\alpha_{Cd^{2+}} &= (1 + K_{f1}[Cl^-] + \beta_2 [Cl^-]^2  + \beta_3[Cl^-]^3 )^{-1}\nonumber
\end{align}\nonumber\]

Solubility and Complexation Examples

Calculate the molar solubility of cadmium sulfide (CdS, Ksp=1x10^-27) in:

1. In pH 5.00 buffer solution
2. In pH 5.00 buffer with 0.100 M Cl^-
3. In pH 5.00 buffer with 1.00 M Cl^-
4. What are [Cd²⁺], [CdCl⁺], [CdCl_2(aq)] and [CdCl₃^-] in the solution from C?

EDTA practice problems

Calculate pNi in a solution made by mixing 50.00 mL of 0.0300 M Ni²⁺ with 50.00 mL of 0.0500 M EDTA at pH = 3.00.

Calculate the equilibrium concentration of Ni2+ in a solution that has [NiY^2-] = 0.0150 at pH = 3.00 and pH = 8.00.

NOTE: the second problem is an equiv point problem!

EDTA Solubility

Calculate the molar solubility of silver chromate in 0.010 F EDTA at pH 7.00, and then at pH 10.00.

EDTA Titration

Consider the titration of 50.00 mL of 0.0100 M Ca²⁺ with 0.0100 F EDTA at pH 10.00… calculate pCa throughout the titration.

(See handout)

EDTA Back-titration

Ni²⁺ can be determined by back titration using standard Zn²⁺ at pH 5.5 with xylenol orange indicator. A solution containing 25.00 mL of Ni²⁺ in dilute HCl is treated with 25.00 mL of 0.05283 EDTA. The solution is neutralized with NaOH, and the pH is adjusted to 5.5 with acetate buffer. The solution turns yellow when a few drops of indicator are added. Titration with 0.02299 M Zn²⁺ requires 17.61 mL to reach the red end point. What is the molarity of Ni²⁺ in the unknown?

Challenge Problem

The following problem is a very nice summary of much of what we have done this semester. Please complete the problem during class time and turn in your answer at the end of class. Feel free to work in your groups.

Consider a 0.100 F citrate buffer at pH 4.800 in equilibrium with solid silver chromate (Ag₂CrO₄). Calculate the solution concentration of all chemical moieties (10 in total).

Contributors and Attributions

• Timothy Strein, Bucknell University ([e-mail])
• Sourced from the Analytical Sciences Digital Library