Chemical Equilibrium (Strein)
- Page ID
- 281946
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Solution Example Problem 1
1) A solution is prepared by dissolving 10.00 ± 0.02 g of K2SO4 into distilled water and that solution is diluted to the mark in a 100.00 mL volumetric flask.
Using the rules for significant figures, and the rules for propagation of uncertainty, calculate:
- The Formality of K2SO4
- The % by weight of K2SO4
(solution density is 1.075 ± 0.003 g/mL) - The molality of K2SO4
…Which method is superior?
Solution Example Problems 2,3
2) What volume of 0.573 F K2SO4 would be needed to prepare 1.00 L of 5.00x10-3 F K2SO4 ?
3) Assuming the 5.00x10-3 F K2SO4 solution above has a density of 1.000 g/mL, calculate the concentration of K+ ions in units of ppm.
Average and Uncertainty
Triplicate measurements (maybe densities, for example…):
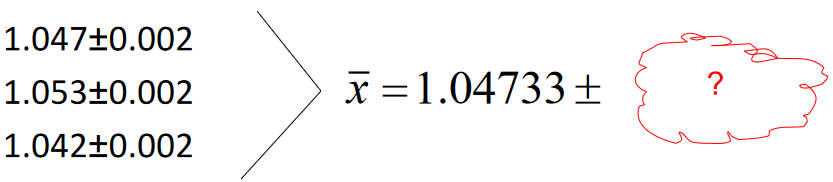
Calculate the average and the associated uncertainty.
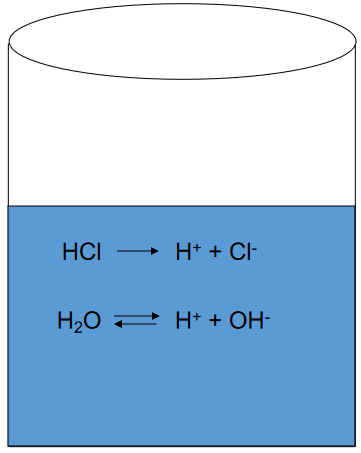
Consider A Strong Acid HCl
(what is the pH?)
|
Concentration of HCl (F HCl = M H+) |
pH = - log([H+]) |
|---|---|
|
1.00x10-1 F |
1.000 |
|
1.00x10-2 F |
2.000 |
|
1.00x10-3 F |
3.000 |
|
1.00x10-4 F |
4.000 |
|
1.00x10-5 F |
5.000 |
|
1.00x10-6 F |
6.000 |
|
1.00x10-7 F |
7.000 |
|
1.00x10-8 F |
8.000 ????!!!!???? |
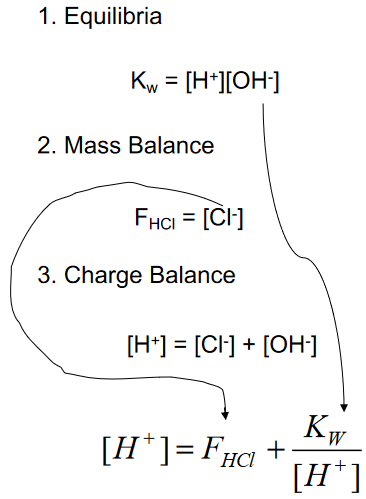
Strong Acids: The Systematic Approach
(multiple equations, as many unknowns)
Consider A Strong Acid HCl
(what is the pH with QUAD?)
|
Concentration of HCl |
pH |
|---|---|
|
1.00x10-1 F |
1.000 |
|
1.00x10-2 F |
2.000 |
|
1.00x10-3 F |
3.000 |
|
1.00x10-4 F |
4.000 |
|
1.00x10-5 F |
5.000 |
|
1.00x10-6 F |
5.996 |
|
1.00x10-7 F |
6.790 |
|
1.00x10-8 F |
6.976 |
Example WA problem
Calculate the pH of a solution that is 0.100 F acetic acid (Ka = 1.75 x 10-5).
Use the “ICE” method to start.
What assumption(s) can be made to make this simple?
Example WB problem
Calculate the pH of a solution that is 0.100 F NH3 (must calculate Kb, given Ka of NH4+ ).
Use the “ICE” method to start.
What assumption(s) can be made to make this simple?
Example mixture problems
(no buffers yet)
- Calculate the pH of a solution prepared by mixing 10.00 mL of 0.100 F acetic acid and 10.00 mL of deionized water.
- Calculate the pH of a solution prepared by mixing 10.00 mL of 0.100 F acetic acid and 10.00 mL of 0.100 F NaOH.
- Calculate the pH of a solution prepared by mixing 10.00 mL of 0.100 F acetic acid and 10.00 mL of 0.200 F NaOH.
Buffer Example problems
- Calculate the pH of a solution prepared by dissolving 0.100 mole of acetic acid and 0.150 mole of sodium acetate into the same 1.00 L solution.
- Calculate the pH of a mixture of 30.00 mL of 0.150 F HNO2 and 20.00 mL of 0.180 F NaNO2.
- Calculate the pH of a mixture of 20.0 mL of 0.112 F HNO2 and 10.00 mL of 0.100 NaOH.
- Calculate the pH of 20.0 mL of 0.012 F HNO2 and 15.0 mL of 0.010 F NaOH.
“Backwards” Buffer Problem
You are asked to make 1.00 L of buffer solution at pH 4.315. You are given a solution of 0.100 F acetic acid and a solution of 0.500 F NaOH. How much of each solution do you need?
A Titration of HA with OH-
Consider the titration of 50.00 mL of 0.100 F Acetic Acid with 0.100 F NaOH. Construct the shape of the titration curve by calculating the pH at various volumes.
Note the pH on the buffer region, at the end point, and on the “final” plateau and generalize these values.
Polyprotic Example Problems
- Calculate the pH of 0.0600 F Oxalic Acid, H2(COO)2.
- Calculate the pH of a 0.0500 F solution of sodium oxalate, Na2(COO)2.
- Calculate the pH of a 0.0500 F solution of monosodium oxalate.
Polyprotic Mixing Problems
(Polyprotics react more than once!)
Calculate the pH of a mixture of 30.00 mL of 0.100 F phosphoric acid with 9.68 mL of 0.500 F NaOH.
“Backwards” Buffer Problems with Polyprotics
(Polyprotics react more than once!)
How many mL of 0.100 F NaOH would you need to add to 100.00 mL of 5.00x10-2 F phthalic acid to result in a buffer at pH 5.00?
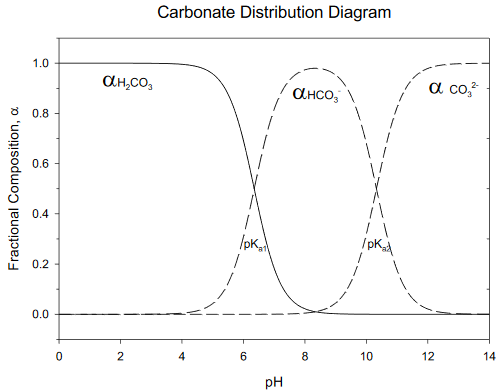
Composition Example Problem
Calculate the fraction of each acid/base form of carbonate at pH= 5.00.
Solubility Calcs
(ignoring side reactions)
- Calculate the solubility of PbI2 in pure water.
- Using the ion product, predict if a precipitate will form when equal volumes of 0.0100 F Pb(NO3)2 and 0.100 F KI are mixed.
Common Ion Example
Calculate the solubility of Ba(IO3)2 in
- pure water
- 0.0200 F KIO3
- 0.00200 F KIO3
pH effect on S
Calculate the solubility of calcium carbonate in:
- Pure water (ignoring side reactions)
- A sol’n that is held at pH = 7.00
- A sol’n that is held at pH = 11.00
Consider S at pH 3.00 …. S = 17 M !? What’s wrong?
Combining common ion and pH effect
Calculate the solubility of silver iodate in 0.010 F KIO3 at pH = 2.00.
Fractional Precipitation
Consider a solution that contains 0.100 M IO3- and 0.100 M SO42- (and 0.300 M Na+). If a solution of 0.100 F Ba(NO3)2 is added, dropwise, what will happen?
Can we quantitatively (99.9%) remove all of the sulfate without removing any of the iodate?
Precipitation Titration
Consider the titration of 10.00 mL of 0.100 F NaCl with 0.100 F AgNO3.
Calculate pAG throughout the range from 0.00 to 20.00 mL.
(what volume is the Veq ?).
Cl- as a ligand for Cd2+
Chloride forms a mono- , di- , and tri-chloride complex with Cd2+
Stepwise formation constants:
Kf1 =101.5 Kf2 =100.4 Kf3 = 100.4
Derive the fraction of free Cd2+ in a solution that contains chloride (αCd2+).
\[\begin{align}
\alpha_{Cd^{2+}} &= (1 + K_{f1}[Cl^-] + K_{f1}K_{f2} [Cl^-]^2 + K_{f1}K_{f2} K_{f3}[Cl^-]^3 )^{-1}\nonumber\\
\alpha_{Cd^{2+}} &= (1 + K_{f1}[Cl^-] + \beta_2 [Cl^-]^2 + \beta_3[Cl^-]^3 )^{-1}\nonumber
\end{align}\nonumber\]
Solubility and Complexation Examples
Calculate the molar solubility of cadmium sulfide (CdS, Ksp=1x10-27) in:
- In pH 5.00 buffer solution
- In pH 5.00 buffer with 0.100 M Cl-
- In pH 5.00 buffer with 1.00 M Cl-
- What are [Cd2+], [CdCl+], [CdCl2(aq)] and [CdCl3-] in the solution from C?
EDTA practice problems
Calculate pNi in a solution made by mixing 50.00 mL of 0.0300 M Ni2+ with 50.00 mL of 0.0500 M EDTA at pH = 3.00.
Calculate the equilibrium concentration of Ni2+ in a solution that has [NiY2-] = 0.0150 at pH = 3.00 and pH = 8.00.
NOTE: the second problem is an equiv point problem!
EDTA Solubility
Calculate the molar solubility of silver chromate in 0.010 F EDTA at pH 7.00, and then at pH 10.00.
EDTA Titration
Consider the titration of 50.00 mL of 0.0100 M Ca2+ with 0.0100 F EDTA at pH 10.00… calculate pCa throughout the titration.
(See handout)
EDTA Back-titration
Ni2+ can be determined by back titration using standard Zn2+ at pH 5.5 with xylenol orange indicator. A solution containing 25.00 mL of Ni2+ in dilute HCl is treated with 25.00 mL of 0.05283 EDTA. The solution is neutralized with NaOH, and the pH is adjusted to 5.5 with acetate buffer. The solution turns yellow when a few drops of indicator are added. Titration with 0.02299 M Zn2+ requires 17.61 mL to reach the red end point. What is the molarity of Ni2+ in the unknown?
Challenge Problem
The following problem is a very nice summary of much of what we have done this semester. Please complete the problem during class time and turn in your answer at the end of class. Feel free to work in your groups.
Consider a 0.100 F citrate buffer at pH 4.800 in equilibrium with solid silver chromate (Ag2CrO4). Calculate the solution concentration of all chemical moieties (10 in total).
Contributors and Attributions
- Timothy Strein, Bucknell University (strein@bucknell.edu)
- Sourced from the Analytical Sciences Digital Library


