Solubility Equilibria – Advanced Topics (Q14 – Q24)
- Page ID
- 199367
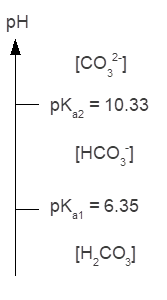
Q14. Calculate the alpha values for the three carbonic acid species (H2CO3, HCO3-, CO32-) at a pH of 6.4. Do these values agree with your predictions based on the carbonic acid ladder diagram?
\[\left[\mathrm{H}^{+}\right]=10^{-\mathrm{pH}}=10^{-6.4}=3.98 \times 10^{-7}\: \mathrm{M}\nonumber\]
\[\begin{array}{rl}
\alpha_{\mathrm{H}_{2} \mathrm{CO}_{3}}
&=\dfrac{\left[\mathrm{H}^{+}\right]^{2}}{\left[\mathrm{H}^{+}\right]^{2}+\left[\mathrm{H}^{+}\right] \mathrm{K}_{\mathrm{a} 1}+\mathrm{K}_{\mathrm{a} 1} \mathrm{K}_{\mathrm{a} 2}} \nonumber\\
&={\dfrac{\left(3.98 \times 10^{-7}\: \mathrm{M}\right)^{2}}{\left(3.98 \times 10^{-7}\: \mathrm{M}\right)^{2}+\left(3.98 \times 10^{-7}\: \mathrm{M}\right)\left(4.47 \times 10^{-7}\right)+\left(4.47 \times 10^{-7}\right)\left(4.68 \times 10^{-11}\right)}} \nonumber\\
&=0.471\nonumber
\end{array}\nonumber\]
\[\begin{array}{rl}
\alpha_{\mathrm{HCO}_{3}^{-}}&=\dfrac{\left[\mathrm{H}^{+}\right] \mathrm{K}_{\mathrm{a} 1}}{\left[\mathrm{H}^{+}\right]^{2}+\left[\mathrm{H}^{+}\right] \mathrm{K}_{\mathrm{a} 1}+\mathrm{K}_{\mathrm{a} 1} \mathrm{K}_{\mathrm{a} 2}} \nonumber\\
&= \dfrac{\left(3.98 \times 10^{-7}\: \mathrm{M}\right)\left(4.47 \times 10^{-7}\right)}{\left(3.98 \times 10^{-7}\: \mathrm{M}\right)^{2}+\left(3.98 \times 10^{-7}\: \mathrm{M}\right)\left(4.47 \times 10^{-7}\right)+\left(4.47 \times 10^{-7}\right)\left(4.68 \times 10^{-11}\right)}\nonumber\\
&=0.529\nonumber
\end{array}\nonumber\]
\[\begin{array}{rl}
\alpha_{\mathrm{CO}_{3}^{2-}}&=\dfrac{\mathrm{K}_{\mathrm{a} 1} \mathrm{K}_{\mathrm{a} 2}}{\left[\mathrm{H}^{+}\right]^{2}+\left[\mathrm{H}^{+}\right] \mathrm{K}_{\mathrm{a} 1}+\mathrm{K}_{\mathrm{a} 1} \mathrm{K}_{\mathrm{a} 2}} \nonumber\\
&={\dfrac{\left(4.47 \times 10^{-7}\right)\left(4.68 \times 10^{-11}\right)}{\left(3.98 \times 10^{-7}\: \mathrm{M}\right)^{2}+\left(3.98 \times 10^{-7}\: \mathrm{M}\right)\left(4.47 \times 10^{-7}\right)+\left(4.47 \times 10^{-7}\right)\left(4.68 \times 10^{-11}\right)}} \nonumber\\
&=0.000062\nonumber
\end{array}\nonumber\]
The calculated fractions of each carbonate species make sense since the pH (6.4) is close to but slightly more basic than the pKa1 (6.35) for carbonic acid. When pH is equal to pKa1, then the fraction of each species involved in the equilibrium described by Ka1 by definition equals 0.50.
Q15. Given that the pH of the Lithia water is 6.4, what is the total concentration of all species in the carbonic acid equilibrium?
The introduction of alpha values enables students to account for the acid-base behavior of ionic species in solution. In the stoichiometric calculations used to determine the concentrations of inorganic constituents in Lithia water (Major Inorganic Constituents – Q3 and Q4), it was determined that the bicarbonate concentration in Lithia water, based on the analysis on the 1915 plaque, was 0.06736 M. Assuming that the pH of the water was 6.4, 52.9% of the species in the carbonic acid equilibrium exist as bicarbonate. Therefore, the total concentration of all species in the carbonic acid equilibrium is:
\[c_T=\dfrac{0.06736\: M}{0.529}=0.1273\: M\nonumber\]
This concentration represents the sum of all carbonate-based species in the carbonic acid equilibrium (i.e. cT = [CO32-] + [HCO3-] + [H2CO3])
Q16. What is the concentration of carbonate ion?
\[\ce{[CO_3^{2-} ]}= \ce{\alpha_{CO_3^{2-}} } c_T=(0.000062)(0.1273M)= 7.92 \times 10^{-6}\: M\nonumber\]
Q17. Using this concentration of carbonate, calculate the concentration of calcium that you would expect in Lithia water from the dissolution of calcium carbonate.
\[\mathrm{K_{sp} = [Ca^{2+}][CO_3^{2-}]}\nonumber\]
\[[Ca^{2+} ][CO_3^{2-} ]=K_{sp}=4.5 \times 10^{-9}\nonumber\]
\[[Ca^{2+} ]= \dfrac{K_{sp}}{[CO_3^{2-} ]} = \dfrac{4.5 \times 10^{-9}}{7.92 \times 10^{-6} }=5.68 \times 10^{-4}\: M \nonumber\]
And the mass solubility (S)
\[\mathrm{S=(5.68 \times 10^{-4}\: M\: Ca^{2+} )\left(\dfrac{40.08\: g\: Ca^{2+}}{1\: mol\: Ca^{2+}}\right)\left(\dfrac{1000\: mg}{1\: g}\right)=22.8\: mg\: L^{-1}}\nonumber\]
Q18. Compare this value to the value of calcium on the plaque.
In the section on Major Inorganic Constituents, the concentration of calcium in Lithia water was determined to be 347 mg L-1. This concentration was based on the analysis engraved on the 1915 plaque. This concentration is approximately fifteen times higher than the calcium ion content calculated in the previous problem, which indicates that the acid-base chemistry of the carbonic acid system is not the only factor that controls the calcium ion concentration in Lithia water. Instructors may want to stress this difference between calculated and determined calcium concentrations as an introduction to the effect of ionic strength on solubility.
Q19. What effect would raising the ionic strength of a solution have on the solubility of a sparingly soluble salt? Think about what relatively high concentrations of other ions (e.g., Na+ and Cl-) might have in a solution containing smaller amounts of Ca2+ and CO32-.
In the case of the solubility of a sparingly soluble salt, analyte ions (Ca2+ and CO32-) experience coulombic interactions with the supporting electrolyte of opposite charge (e.g. CO32- ions interact with Na+, and Ca2+ ions interact with Cl-) . The ions from the supporting electrolyte partially screen the charge of each analyte ion. These interactions decrease the activity, or the effective concentration, of the analyte ions.The solubility equilibrium and equilibrium constant expression of calcium carbonate is expressed by:
\[\ce{CaCO3 (s) \rightleftharpoons Ca^2+ (aq) + CO3^2- (aq)} \hspace{20px} K_{sp}=a_{Ca^{2+}}a_{CO_3^{2-}}\nonumber\]
As the ionic strength of a solution increases, the screening of the analyte ions increases, and the analyte ion activity decreases. According to LeChatelier’s principle, if the activity of the dissolved ions decreases, then more of the solid should dissolve so that the product of the calcium ion and carbonate ion concentrations once again equals the solubility product. Instructors should keep in mind that students do not need to know the Debye-Hückel equation in order to answer this question.
Q20. Calculate the molar solubility of AgCl under infinite dilution conditions (i.e. µ = 0) with its solubility in 0.10 M NaNO3. The hydrated ion diameters and thermodynamic equilibrium constants may be obtained from Analytical Chemistry 2.0.
\[\ce{AgCl(s) \rightleftharpoons Ag+ (aq) + Cl- (aq)} \hspace{20px} \mathrm{K_{sp} = [Ag^+][Cl^-] = 1.8 \times 10^{-10}}\nonumber\]
Under infinite dilution conditions:
\[\mathrm{K_{sp} = [Ag^+][Cl^-] = 1.8 \times 10^{-10}}\nonumber\]
Let X be the molar solubility of AgCl
\[\mathrm{[Ag^+][Cl^-] = (X)(X) = X^2 = 1.8 \times 10^{-10}}\nonumber\]
\[\mathrm{X = 1.34 \times 10^{-5}\: M}\nonumber\]
Taking ionic strength into account:
- Calculation of ionic strength (µ)
- Calculation of activity coefficients (γ) using Debye – Hückel equation
\[\log γ_x= \dfrac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}\nonumber\]
\[γ_{Ag^+} = \mathrm{10^{\Large\frac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}}= 10^{\Large\frac{(-0.51)(1^2 ) \sqrt{0.10}}{1+3.3(0.25\: nm) \sqrt{0.10}}}} = 0.7449 \nonumber\]
\[γ_{Cl^-} \mathrm{= 10^{\Large\frac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}}= 10^{\Large\frac{(-0.51)(-1^2 ) \sqrt{0.10}}{1+3.3(0.3\: nm) \sqrt{0.10}}}}=0.7537\nonumber\]
- Calculation of a concentration-based solubility productand molar solubility of AgCl
- \(K_{sp}^{'} = \dfrac{K_{sp}}{γ_{Ag^+} γ_{Cl^-} }=\dfrac{1.8 \times 10^{-10}}{(0.7449)(0.7537)} =3.2 \times 10^{-10}\)
- \(X^2=3.2 \times 10^{-10}\)
- \(X=1.79 \times 10^{-5}\: M\)
Q21. Calculate the concentration-based equilibrium constant for CaCO3, H2CO3, and HCO3-, and use these constants to predict the calcium concentration in Lithia water at pH 6.4. The ionic strength of Lithia water may be calculated from the solute molarities reported on the plaque from the Major Inorganic Constituents section, and the hydrated ion diameters and thermodynamic equilibrium constants may be obtained from Analytical Chemistry 2.0.
For the solubility equilibrium
\[\ce{CaCO3 (s) ⇌ Ca^2+ (aq) + CO3^2- (aq)}\nonumber\]
Taking ionic strength into account:
- Calculation of ionic strength (µ): This calculation involves the analyte molarities that were calculated from the 1915 analysis of Lithia water.
- \(μ= \dfrac{1}{2} \sum c_i z_i^2
=\dfrac{1}{2}
\begin{pmatrix} (0.1114\: M\: Na^+ ) (+1)^2 + (0.002792\: M\: K^+ ) (+1)^2 + (0.002263\: M\: Li^+ ) (+1)^2 + \\
(0.00866\: M\: Ca^{2+} ) (+2)^2 + (0.00788\: M\: Mg^{2+} ) (+2)^2 + \\
(0.0001566\: M\: Fe^{2+}) (+2)^2 + (0.07726\: M\: Cl^- ) (-1)^2 + \\
(0.06736\: M\: HCO_3^- ) (-1)^2 + (0.004883\: M\: BO_2^- ) (-1)^2 + \\
(0.00002742\: M\: SO_4^{2-} ) (-2)^2 + (0.00158\: M\: SiO_3^{2-} ) (-2)^2 \end{pmatrix}
= 0.170\)
- \(μ= \dfrac{1}{2} \sum c_i z_i^2
- Calculation of activity coefficients (γ) using the Debye – Hückel equation for inorganic salt
\[\mathrm{\log γ_x= \dfrac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}}\nonumber\]
\[γ_{Ca^{2+}}
= \mathrm{10^{\Large\frac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}}}
= \mathrm{10^{\Large\frac{(-0.51)(2^2 ) \sqrt{0.170}}{1+3.3(0.60\: nm) \sqrt{0.170}}}}
=0.3443\nonumber\]
\[γ_{CO_3^{2-}}
= \mathrm{10^{\Large\frac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}}}
= \mathrm{10^{\Large\frac{(-0.51)(-2^2 ) \sqrt{0.170}}{1+3.3(0.45\: nm) \sqrt{0.170}}}}
=0.3008\nonumber\]
For the weak acid equilibria
\[\ce{H2CO3 (aq) ⇌ H+ (aq) + HCO3- (aq)} \hspace{20px} K_{a1}=4.47 \times 10^{-7}=\dfrac{[H^+ ][HCO_3^- ]}{[H_2 CO_3 ]}\nonumber\]
\[\ce{HCO3- (aq) ⇌ H+ (aq) + CO3^2- (aq)} \hspace{20px} K_{a2}=4.68 \times 10^{-11}=\dfrac{[H^+ ][CO_3^{2-} ]}{[HCO_3^- ] }\nonumber\]
- Calculation of activity coefficients (γ) using Debye – Hückel equation for weak acid
\[γ_{H^+}
= \mathrm{10^{\Large\frac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}}}
= \mathrm{10^{\Large\frac{(-0.51)(+1^2 ) \sqrt{0.170}}{1+3.3(0.9\: nm) \sqrt{0.170}}}}
=0.8044\nonumber\]
\[γ_{CO_3^{2-}}
= \mathrm{10^{\Large\frac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}}}
= \mathrm{10^{\Large\frac{(-0.51)(-2^2 ) \sqrt{0.170}}{1+3.3(0.45\: nm) \sqrt{0.170}}}}
=0.3008\nonumber\]
\[γ_{HCO_3^- }
= \mathrm{10^{\Large\frac{-0.51 z^2 \sqrt{μ}}{1+3.3α_x \sqrt{μ}}}}
= \mathrm{10^{\Large\frac{(-0.51)(-1^2 ) \sqrt{0.170}}{1+3.3(0.45\: nm) \sqrt{0.170}}}}
=0.7406\nonumber\]
- Calculation of a concentration-based acid dissociation constant and the molar concentration of the carbonate ion
\[K_{a2}^{'}
= \dfrac{K_{a2} γ_{HCO_3^- }}{γ_{H^+} γ_{CO_3^{2-} }}
= \dfrac{(4.68 \times 10^{-11} )(0.7406)}{(0.8044)(0.3008)}
=1.43 \times 10^{-10}\nonumber\]\[1.43 \times 10^{-10}= \dfrac{[H^+ ][CO_3^{2-} ]}{[HCO_3^- ]} \nonumber\]
Based on the 1915 analysis, [HCO3-] = 0.06736 M, and assuming that the pH is 6.4 ([H+] = 3.98 x 10-7 M):
\[1.43 \times 10^{-10}= \dfrac{(3.98 \times 10^{-7}\: M)[CO_3^{2-} ]}{(0.06736\: M)}\nonumber\]
\[2.42 \times 10^{-5}\: M=[CO_3^{2-} ]\nonumber\]
- Calculation of a concentration-based solubility product and both the molar solubility and mass solubility for calcium carbonate in Lithia water
- \(K_{sp}^{'}= \dfrac{K_{sp}}{γ_{Ca^{2+}} γ_{CO_3^{2-}} }=\dfrac{4.5 \times 10^{-9}}{(0.3443)(0.3008)} =4.35 \times 10^{-8}\)
- \(K_{sp}^{'}=[Ca^{2+} ][CO_3^{2-} ]\)
- \(4.35 \times 10^{-8}=[Ca^{2+} ](2.42 \times 10^{-5}\: M)\)
- \([Ca^{2+} ]=1.79 \times 10^{-3}\: M\)
- \(S_{CaCO_3} = 1.79 \times 10^{-3}\: M\left(\dfrac{100.09\: g\: CaCO_3}{mol}\right)\left(\dfrac{1000\: mg}{g}\right)=\dfrac{179.6\: mg\: Ca^{2+}}{L}\)
Students should be able to communicate that although the mass solubility of calcium carbonate in Lithia water is within a factor of two of the reported solubility from the 1915 analysis, there still may be another factor left unexplained which would account for the additional calcium in the Lithia water.
Q22. Remembering that the Lithia water contains carbonate ion, use LeChatelier’s principle to explain what effect the addition of carbonic acid has on the concentration of carbonate ion in Lithia water?
The carbonate buffer system consists of carbonic acid, hydrogen carbonate ion (bicarbonate), and the carbonate ion, and all three of these chemical species contain the carbonate ion. Carbonic acid is the fully protonated form in the buffer system and carbonate ion is the fully deprotonated form in the buffer system. When carbonic acid is introduced to a solution containing carbonate ion, the dissociation of protons from carbonic acid shifts the carbonate equilbrium in Lithia water favoring the protonation of carbonate ion to form bicarbonate ion:
\[\ce{H3O+ (aq) + CO3^2- (aq) ⇌ HCO3- (aq) + H2O (l)}\nonumber\]
This reaction decreases the concentration of the carbonate ion in solution.
Q23. Considering your answer to the preceding question, what effect would the addition of carbonic acid have on the solubility of calcium carbonate and other sparingly soluble carbonate salts?
For the solubility equilibrium
\[\ce{CaCO3 (s) ⇌ Ca^2+ (aq) + CO3^2- (aq)}\nonumber\]
The addition of carbonic acid would reduce the carbonate ion concentration. Based on Le Chatelier’s principle, if the concentration of a product is decreased in a chemical equilibrium, then the equilibrium would shift towards the products to reestablish equilibrium. This shift in the solubility equilibrium of calcium carbonate would increase the solubility of calcium carbonate.
Q24. The concentration of calcium ion based on the 1915 analysis of Lithia water is 347 mg L-1. Assuming that the calcium ion concentration in Lithia water is controlled by the carbonate ion concentration in Lithia water, calculate the carbonate ion concentration in Lithia water using the concentration-based equilibrium constant for calcium carbonate.
From Q21 (Solubility Equilibria):
- \(K_{sp}^{'}= \dfrac{K_{sp}}{γ_{Ca^{2+}} γ_{CO_3^{2-}} }=\dfrac{4.5 \times 10^{-9}}{(0.3443)(0.3008)} =4.35 \times 10^{-8}\)
- \(K_{sp}^{'}=[Ca^{2+} ][CO_3^{2-} ]\)
From Q3 (Major Inorganic Constituents):
- \(4.35 \times 10^{-8}=(8.66 \times 10^{-3}\: M)[CO_3^{2-} ]\)
- \([CO_3^{2-} ]=5.02 \times 10^{-6}\: M\)


