Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Introduction to Mass Spectrometry

Last updated

Dec 3, 2020
Save as PDF
- Introduction to Chromatography
- Ionic Strength and Activity

Chrisi Hughey
Analytical Sciences Digital Library

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Part 1. The mass spectrum

Learning Objectives

At the completion of this activity, you should be able to…

describe the relationship between the peak height in the mass spectrum and the natural abundance of isotopes
differentiate between average mass, isotopic mass and nominal mass; identify the appropriate use of each in the analysis of mass spectrometric data
identify the molecular ion in the mass spectrum
identify the base peak in the mass spectrum

Mass spectrometry is routinely used for the identification and quantitation of small organic molecules composed of carbon, hydrogen and oxygen.

Consider this…

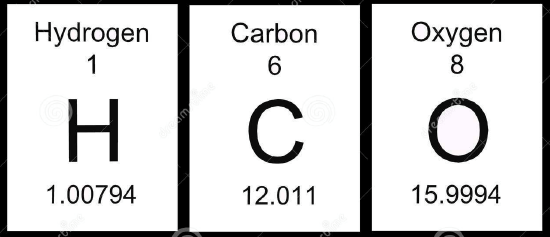
Table 1 – Isotopic Masses

Element	Isotopic Mass (Da)	% Abundance
¹H	1.00782	99.99
¹²C	12.0000	98.93
¹⁶O	15.9949	99.76

Compare the masses of hydrogen, carbon and oxygen from the periodic table (above) to the masses in Table 1.

Calculate the differences between the masses in the periodic table and the masses in Table 1.
What correlation exists between the differences calculated in Q1 and the percent abundance in Table 1?
Use your knowledge from general chemistry to explain how the masses on the periodic table are different from the masses in Table 1.
A simulated mass spectrum of carbon is shown in Figure 1. What mass (average or isotopic) is useful in mass spectrometry? Explain.

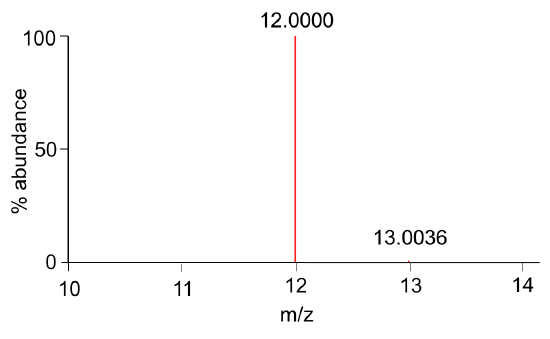
Figure 1. Mass spectrum of carbon.

Now let’s look at the axes in the mass spectrum…

What is the y-axis? What correlation exists between peak heights in Figure 1 and the relative abundances in Table 1?
What is the x-axis? Compare the expected mass (Table 1) and the observed mass (Figure 1). What is implied about “z”?

Consider this… The peak with the greatest abundance in the mass spectrum is called the base peak.

What is the base peak in Figure 1?

Consider this…

Table 2. Benzoic Acid

Formula	Average mass	122.1234 Da
C₇H₆O₂	Isotopic mass	122.0367 Da
C₇H₆O₂	Nominal mass	122 Da

Use Table 1 with the most abundant isotopes of carbon, hydrogen and oxygen to calculate the isotopic mass for benzoic acid, C₇H₆O₂. Check your answer in Table 2.
Calculate the difference between the mass calculated in Q8 and the mass observed for the most abundant peak in Figure 2. This data was “collected” on a high mass accuracy instrument.

Consider this… for an analyte to be detected by a mass spectrometer, it must be in the gas phase and have charge. The analyte is charged (ionized) in the ionization source of the mass spectrometer. In Figure 2, benzoic acid was ionized by electron ionization (EI). In this process, an electron is lost to form a radical cation (M^+•). The mass difference calculated in Q9 corresponds to the mass of the electron lost. This process is shown generically:

$\ce{M → M^{+•} + e-}\nonumber$

Assign a formula to both ions observed in Figure 2. Be sure to represent the ions as charged species.

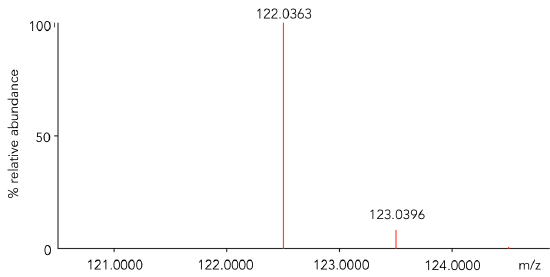
Figure 2. Zoomed mass inset of benzoic acid obtained on a high mass accuracy instrument with an EI source.

Consider this… Only the highest mass accuracy instruments can accurately measure the loss of an electron. Therefore, for most applications we assume

$\mathbf{M^{+•} = M}\nonumber$

and call the M^+• peak the molecular ion. It provides the molecular mass of the analyte.

To date, most of the mass spectra that you have seen were collected on a low resolution, low mass accuracy GC/MS. An example is shown below in Figure 3.

**Figure 3.** Mass spectrum of benzoic acid obtained on a low mass accuracy instrument with an EI source.

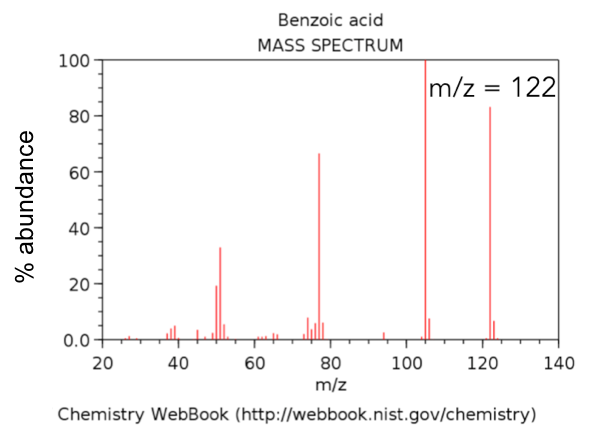
Circle the molecular ion of benzoic acid in Figure 3. Use Table 2 to classify the observed mass as the average mass, the isotopic mass or the nominal mass.
Explain how nominal mass is determined.
When interpreting mass spectra, when is it appropriate to use the average mass, the isotopic mass or the nominal mass?

Part 2. Figures of merit in mass spectrometry

Learning Objectives

At the completion of this activity, you should be able to…

calculate mass accuracy from mass spectral data
classify mass analyzers as low or high mass accuracy
calculate mass resolving power from mass spectral data
classify mass analyzers as low, medium or high resolving power

Consider this…

The heart of a mass spectrometer is the mass analyzer, which differentiates analytes based on their mass-to-charge ratios (m/z). Numerous figures of merit are used to describe the performance of a mass analyzer, including scan speed, mass range, linear dynamic range, sensitivity, mass accuracy, mass resolving power and mass resolution. Typical figures of merit for mass accuracy and mass resolving power are given in Table 3.

Table 3. Approximate figures of merit for different mass analyzers.*

Mass Analyzer	Mass accuracy (ppm)	Mass resolving power (m/Δm)
quadrupole	1000 ppm	1,000
ion trap	1000 ppm	1,000
time of flight	~ 10 ppm	10,000
high res time of flight	~ 10 ppm	60,000
Orbitrap	~ 3 ppm	100,000 – 500,000
Fourier transform ion cyclotron resonance (FT-ICR)	< 1 ppm	200,000 – 1,000,000

*Manufacturers continuously improve instruments. These figures are ball-park estimates.

Mass Accuracy

You are familiar with the concept of “accuracy.” Give the formula used to calculate accuracy.
Most mass spectrometers measure mass very accurately. Therefore, the difference between measured and observed mass is quite small. For this reason, mass accuracy is often expressed in parts per million (ppm). Rewrite the equation in Q1 so that the calculated result will have a unit of ppm.
Using the equation in Q2, calculate the mass accuracy of benzoic acid from the mass spectral data shown in Figure 4. Recall that you calculated in theoretical mass of benzoic acid in Part 1, Q8.

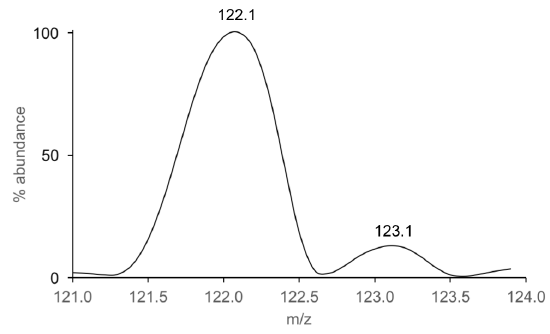
Figure 4. Zoomed mass inset of benzoic acid obtained on an instrument with an EI source.

Based on your answer in Q4, what instrument was likely used to collect the data in Figure 4?
In Part 1 of this module, we saw that molecular ions are formed by loss an electron (mass = 0.0004 Da). Which mass spectrometer(s) listed in Table 3 has/have the mass accuracy needed to detect the loss of a single electron from benzoic acid?
Classify the mass analyzers in Table 3 as low or high mass accuracy instruments.

Low Mass Accuracy Instruments	High Mass Accuracy Instruments

Mass Resolving Power

Consider this… Mass resolving power (RP) describes the separation between two adjacent peaks whose overlap is 10% (see the dotted lines in Figure 5). It is calculated using:

$\textit{mass resolving power} = \dfrac{m}{Δm}\nonumber$

There are numerous ways to calculate mass resolving power with this equation. We are going to utilize the most straightforward method, where m is the mass of the ion (e.g., 1000) and Δm is the width of the peak at full width half-height (or width at 50% of maximum peak height). Using the left-most peak in Figure 5, the RP is

$\textit{mass resolving power} = \dfrac{1000.0\: Da}{\sim 0.5\: Da} = {\sim 2000}\nonumber$

Note that mass resolving power is a unitless value.

**Figure 5.** Two adjacent mass spectral peaks at m/z ~1000. *Adapted from Robinson*.¹

Use the molecular ion of benzoic acid (Figure 4) to estimate the mass resolving power of that mass analyzer.
When reporting mass resolving power, the analyst must specify the m/z used in the calculation. Why do you think this is important? Support your answer with evidence.
An FT-ICR with a 11T magnet can achieve a mass resolving power of 1,000,000 at m/z 400. What is the smallest mass difference that can be resolved?

Classify the mass analyzers in Table 3 as low, medium or high mass resolving power.

Low RP	Med RP	High RP

Table 4 lists the approximate cost for different mass analyzers. Describe the relationship that exists between mass accuracy, resolving power and cost.

Table 4. costs for different mass analyzers.*

Mass Analyzer	Cost
quadrupole	$75,000
ion trap	$75,000
time of flight	$150,000
high res time of flight	$400,000
Orbitrap	$750,000
Fourier transform ion cyclotron resonance	$1,000,000

*These are ball-park figures. Cost vary considerably by manufacturer.

Part 3. Hard vs. soft ionization

Learning Objectives

At the completion of this activity, you should be able to…

identify the types of ions formed by EI and ESI
use mass spectral data to classify ionization sources as soft ionization or hard ionization
describe the advantages and disadvantages of soft and hard ionization

Consider this… There are MANY different types of ionization sources. Electron ionization is the most common source coupled to GC. Electrospray ionization (ESI) is the common most source coupled to LC. (We will discuss why later). Let’s look the types of ions produced by EI and ESI by comparing mass spectra of benzoic acid.

**Figure 3 (revisited).** Mass spectrum of benzoic acid obtained on a low mass accuracy instrument with an EI source. Data is shown in centroid mode (peaks are deduced to “sticks” at the center of mass).

**Figure 6.** Mass spectrum of benzoic acid obtained on a low mass accuracy instrument with an ESI source. Data is shown in profile mode.

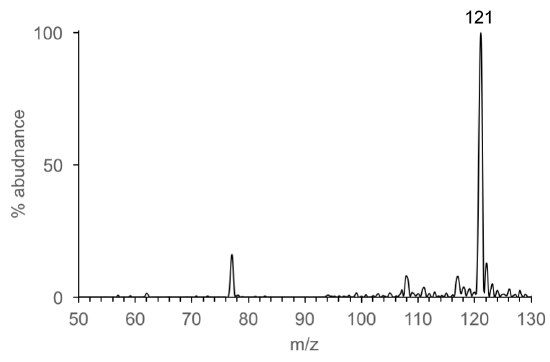
Identify the mass and type of ion that corresponds to benzoic acid (C₇H₆O₂) in each mass spectrum. Explain how the mass of benzoic acid is determined from the EI mass spectrum and from the ESI mass spectrum.

The most abundant ions (>20% abundance) observed in the EI and ESI mass spectra are listed in Table 5. How are the EI and ESI spectra different? How are they the same?

Table 5. Most abundant ions in EI and ESI

EI Mass Spectrum	ESI Mass Spectrum
122 105 77 51 50	121 77

EI Mass Spectrum

ESI Mass Spectrum

122

105

121

1. Draw the structure of benzoic acid.
2. Use the structure to propose the identity of the peaks in the mass spectra.
EI is classified as a “hard ionization” source, while ESI is classified as a “soft ionization” source. Use your answers in Q1-3 to construct a definition for hard ionization and soft ionization.
Chemical ionization (CI) is a soft ionization technique used with GC. From the mass spectra of 1-decanol, determine the advantages and disadvantages of hard and soft ionization.

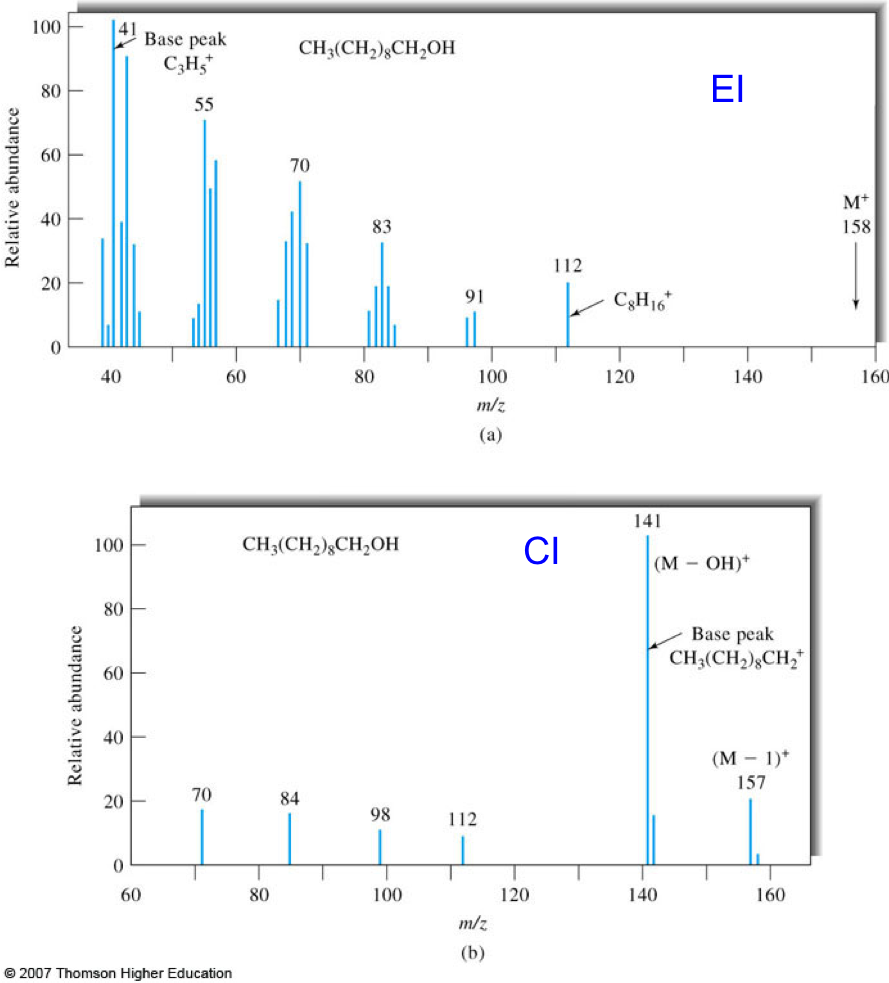
Figure 7. Mass spectra of 1-decanol obtained by EI (top) and CI (bottom) GC/MS. Figures taken from Skoog.²

References

Skoog, D.A., Holler, F.J., Crouch, S.R. Principles of Instrumental Analysis, 6^th edition; Cengage Learning, Boston, 2006.
Robinson, J. W., Frame, E.M.S, Frame, G.M. Undergraduate Instrumental Analysis, 7^th edition, CRC Press, Boca Raton, 2014.

Contributors and Attributions

Chrisi Hughey, James Madison University (hugheyca@jmu.edu)
Sourced from the Analytical Sciences Digital Library

Part 1. The mass spectrum

Part 2. Figures of merit in mass spectrometry

Mass Accuracy

Mass Resolving Power

Part 3. Hard vs. soft ionization

References

Contributors and Attributions

Support Center

How can we help?