Determinants (Worksheet)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

In quantum mechanics, we sometimes encounter problems in which we need to solve a series of linear equations simultaneously. For this, using the framework of linear algebra and determinants is very useful.

Systems of Linear Equations

Consider the two equations

\[ax+by=c \label{eq01}\]

and

\[dx+ey=f. \label{eq02}\]

Since these equations represent two lines in the xy-plane, the simultaneous solution of these two equations (i.e. points \((x,y)\) that satisfy both equations) is merely the intersection of the two lines. The graphs below illustrate the three scenerios: non-parallel lines, parallel (but not identical) lines, and identical lines.

Figure \(\PageIndex{1}\): Remember, when solving a system of linear equations, we are looking for points the two lines have in common. Typically, there are three types of answers possible. (CC-BY 4.0; Openstax).

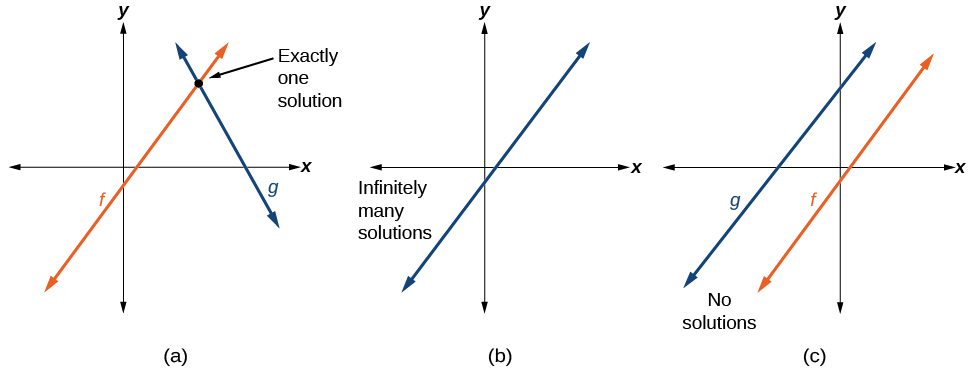
From left to right these cases yield one solution, no solutions, and infinite solutions. The same situation occurs in three dimensions; the solution of 3 equations with 3 unknowns is the intersection of the 3 planes. The determinant is a simple tool for determining the number of solutions of a square system of equations.

It is often convenient to represent a system of equations as a matrix equation or even as a single matrix. Consider the system of equations

\[2x+3y=-8 \label{eq1}\]

and

\[-x+5y=1. \label{eq2}\]

The left hand side of Equations \ref{eq1} and \ref{eq2} can be expanded in terms of the coefficients of \(x\) and \(y\)

\[ \begin{pmatrix} 2x+3y \\ -x + 5y \end{pmatrix}= \begin{pmatrix}
2 & 3 \\
-1 & 5
\end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix} \label{Matrix1} \]

Q1

Verify Equation \ref{Matrix1} using matrix multiplication.

Full Equation

We can equate Equation \ref{Matrix1} to the right hand side of Equations \ref{eq1} and \ref{eq2} and represent it as a matrix equation:

\[ \begin{pmatrix}
2 & 3 \\
-1 & 5
\end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix} -8 \\ 1 \end{pmatrix} \]

or

\[AX=B \label{matrix}\]

where

\[ \begin{align} A &= \begin{pmatrix}
2 & 3 \\
-1 & 5
\end{pmatrix} \\[5pt] X &= \begin{pmatrix}
x \\
y
\end{pmatrix} \\[5pt] B &= \begin{pmatrix}
-8 \\
1
\end{pmatrix} \end{align}\]

The \(2x2\) matrix \(A\) is called the matrix of coefficients of the system of equations. We can solve this matrix equation for \(x\) and \(y\) with Gaussian elimination or via direct substitution of one equation into the other. This representation can also be done for any number of equations with any number of unknowns. Equation \ref{matrix} represents a homogeneous system of equations if \(B\) is the \(n \times 1\) vector of zeros. Otherwise, the equation is called nonhomogeneous.

System of Equations

Consider the following nonhomogeneous system of equations:

\[ax+by=c \label{Ex1}\]

\[dx+ey=f \label{Ex2}\]

where all the variables are are scalars.

Q2

How can you manipulate these two expressions to get an expression that only depends on \(x\)?

Q3

Using this method, what is the expression you get when you isolate \(x\) on one side of the equation? That is, what is the expression that describes \(x\)?

Q4

What is the corresponding expression for \(y\)?

Cramer's Rule

For square systems of equations (i.e. those with an equal number of equations and unknowns), the most powerful tool for determining the solutions of the system is the determinant. Suppose we have a system of two equations and two unknowns like in Equations \ref{eq01} and \ref{eq02} where both \(c\) and \(f\) are non-zero (i.e. the system is nonhomogeneous). These are equations of two lines (in 2D) with slope \(-a/b\) and \(-d/e\), respectively. For this system

\[A = \begin{pmatrix}
a & b \\
d & e
\end{pmatrix}\]

We can define the determinant of a \(2 \times 2\) system of linear equations to be the determinant of the matrix of coefficients \(A\) of the system.and we can define a determinant for this system as

\[ \begin{aligned}|A|={\begin{vmatrix}a&b\\d&e\end{vmatrix}}=ae-bd.\end{aligned}\]

Q5

Compare the determinant of the matrix \(A \) with the solutions you found in Q3 and Q4. What do you see?

Q6

Cramer's Rule is a method of solving systems of linear equations using determinants that is an easier way of expressing the solutions you found in Q3 and Q4. For the systems of equations:

\[x = \dfrac{\begin{vmatrix}c&b\\f&e\end{vmatrix}}{\begin{vmatrix}a&b\\d&e\end{vmatrix}}\]

\[y = \dfrac{\begin{vmatrix}a&c\\d&f\end{vmatrix}}{\begin{vmatrix}a&b\\d&e\end{vmatrix}}\]

The solutions are are constructed with the denominator in each expression as the determinant of the coefficient matrix \(A\) and the numerator is the determinant of this matrix with the column vector for the variable replaced with the solution vector \(B\).

Solve the system of equations, using Cramer's Rule.

Properties of Cramer's Rule and Systems of Equations

Cramer's Rule can be extended to any number of variables and equations as long as the system is square - the same number of variables and equations. An underdetermined system has less equations than unknowns and an overdetermined system has more equations than unknowns. For a system with 3 equations and 3 unknowns

\[ax + by + cz =j \]

\[dx + ey + fz = k \]

\[gx + hy + iz = l \]

\[x = \dfrac{\begin{vmatrix}j&b&c\\k&e&f\\l&h&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}\]

Q7

Write the forms of the solutions for \(y\) and \(z\) given the system above.

Q8

In any system of equations the nature of the determinant of the coeffcients reveals the type and quantity of the solutions. What property does the determinant of \(A\) need to have for a solution?

\[ \begin{aligned}|A|={\begin{vmatrix}a&b\\d&e\end{vmatrix}}=ae-bd.\end{aligned}\]

Suppose this determinant is zero. Then

\[ ae-bd = 0\]

or alternatively

\[\dfrac{a}{b}=\dfrac{d}{e}\]

In other words, the slopes are equal; this means the lines are either identical (there is an infinite number of solutions like in Figure \(\PageIndex{1b}\) or parallel (there are no solutions like in Figure \(\PageIndex{1c}\)). If the determinant is non-zero, then the slopes must be different and the lines must intersect in exactly one point (see Figure \(\PageIndex{1a}\)). This leads us to the following statement:

A \(n \times n\) nonhomogeneous system of linear equations has a unique non-trivial solution if and only if its determinant is non-zero. If this determinant is zero, then the system has either no nontrivial solutions or an infinite number of solutions.

Homogeneous Systems of Equations

We have seen how the determinant of the coefficients in a nonhomogeneous system of equations reveals the nature of the solution to that system. What about homogenous equations? A homogenous linear system of equations is one in which the solutions vector is \(0\).

Q9

Apply Cramer's Rule to the system of equations in Q6 if it was a homogenous system - \(c = 0\) and \(f = 0\).

What happens if \(det(A) \neq 0\)?

What happens if \(det(A) = 0\)?

A \(n \times n\) homogeneous system of linear equations has a unique non-trivial solution if and only if its determinant is zero. If this determinant is non-zero, then the system has either no nontrivial solutions or an infinite number of solutions.

Cofactors and Expansions

We introduce the concept of a cofactor as a way to expand arbitrary \(n \times n\) determinants. The cofactor \(A_{ij}\) of an element is a \((n-1) \times (n-1)\) determinant left over when we delete the \(i\)th row and \(j\)th column from the determinant and multiply by \((-1)^{i+j}\).

\[\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,\overbrace{\begin{vmatrix}e&f\\h&i\end{vmatrix}}^{\text{cofactor for }a}-b\,\overbrace{\begin{vmatrix}d&f\\g&i\end{vmatrix}}^{\text{cofactor for }b}+c\,\overbrace{\begin{vmatrix}d&e\\g&h\end{vmatrix}}^{\text{cofactor for }c}\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}\]

Q10

For the matrix below, what is the cofactor of \(a_{12}\)?

\[\begin{vmatrix}
a_{11} &a_{12} &a_{13} \\
a_{21} &a_{22} &a_{23} \\
a_{31} &a_{32} &a_{33}
\end{vmatrix}\]

Q11

Sometimes we want to solve a determinantal equation, e.g,

\[\begin{vmatrix}
x &1 &0 &0 \\
1 &x &1 &0 \\
0 &1 &x &1 \\
0 &0 &1 &x
\end{vmatrix}=0\]

Use cofactors to simplify and solve this problem (for \(x\))?